专题19《组合图形的认识、表面积与体积》 ——2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义（原卷版+解析版）

这是一份专题19《组合图形的认识、表面积与体积》 ——2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义（原卷版+解析版），文件包含专题19《组合图形的认识表面积与体积》2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义解析版docx、专题19《组合图形的认识表面积与体积》2022-2023学年小学数学六年级下册小升初全国通用版专题复习讲义原卷版docx等2份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。
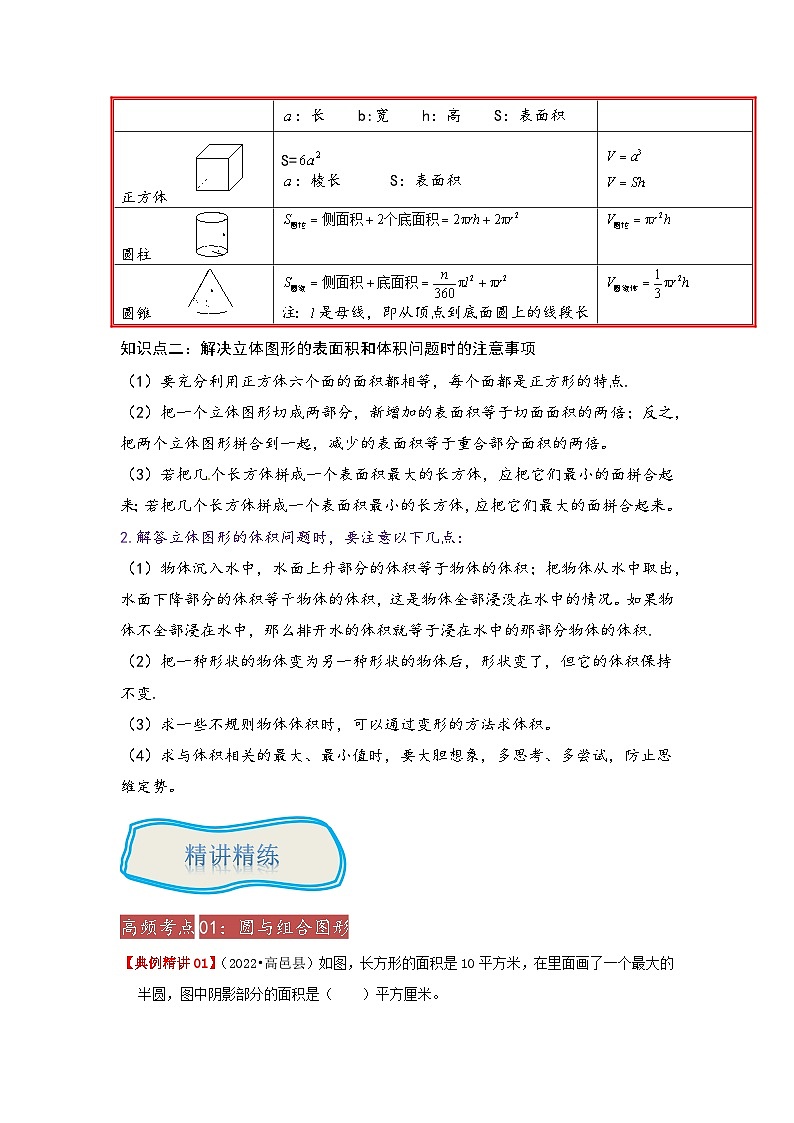
2022-2023学年小升初数学举一反三重难点培优讲义专题19 组合图形的认识、表面积与体积小学阶段所学的立体图形主要有长方体、正方体、圆柱体和圆锥体，这四种立体图形的表面积和体积的计算是小升初数学的热点内容，特别是涉及到立体图形的切拼时，立体图形的表面积和体积发生了变化，牢固掌握这些立体图形的特征和有关的计算方法及切拼时表面积和体积的变化规律是解题的关键，本讲将在前面两讲学习的基础上进一步总结整理立体图形切拼时表面积和体积的变化规律。知识点一：立体图形的表面积和体积计算常用公式：立体图形表面积体积长方体  S=2   ：长    b:宽    h：高    S：表面积正方体  S=：棱长      S：表面积圆柱     圆锥    注：是母线，即从顶点到底面圆上的线段长知识点二：解决立体图形的表面积和体积问题时的注意事项（1）要充分利用正方体六个面的面积都相等，每个面都是正方形的特点.（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍；反之，把两个立体图形拼合到一起，减少的表面积等于重合部分面积的两倍。（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来；若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。2.解答立体图形的体积问题时，要注意以下几点：（1）物体沉入水中，水面上升部分的体积等于物体的体积；把物体从水中取出，水面下降部分的体积等干物体的体积，这是物体全部浸没在水中的情况。如果物体不全部浸在水中，那么排开水的体积就等于浸在水中的那部分物体的体积.（2）把一种形状的物体变为另一种形状的物体后，形状变了，但它的体积保持不变.（3）求一些不规则物体体积时，可以通过变形的方法求体积。（4）求与体积相关的最大、最小值时，要大胆想象，多思考、多尝试，防止思维定势。高频考点01：圆与组合图形【典例精讲01】（2022•高邑县）如图，长方形的面积是10平方米，在里面画了一个最大的半圆，图中阴影部分的面积是（　　）平方厘米。A．5 B．3.14 C．2.5 D．2.15【思路点拨】观察图形可得，长方形内最大的圆的直径是这个长方形的长，半径就是这个长方形的宽，设半圆的半径为r厘米，则长方形的长为2r厘米，宽为r厘米，根据长方形的面积公式即可求得r2的值，从而求得半圆的面积。【规范解答】解：设半圆的半径为r米，则长方形的长为2r米，宽为r米，根据长方形的面积公式可得：2r×r＝10  2r2＝10   r2＝5则这个半圆的面积为：3.14×5÷2＝7.85（平方厘米）阴影部分的面积为：10﹣7.85＝2.15（平方厘米）答：图中阴影部分的面积是2.15平方厘米。故选：D。【考点评析】根据长方形内最大的半圆得出长方形的长和宽分别是半圆的直径和半径的长度，从而求得半径的平方是本题的关键。【举一反三01】．（2020•无锡）如图，大正方形的面积是10平方厘米，依次连接正方形各边的中点，那么，大圆与小正方形的面积比是（　　）A．2π：1 B．4：1 C．π：1 D．8：1【思路点拨】如上图所示，把大正方形平均分成8份，那么小正方形的面积就等于大正方形面积的一半，即10÷2＝5平方厘米；同时，大正方形的对角线就相当于圆的直径，设圆的半径是r厘米，那么可得：2r×r÷2×2＝10，由此求出r2＝5，然后根据圆的面积公式S＝πr2求出圆的面积，再求出大圆与小正方形的面积比即可．【规范解答】解：设圆的半径是r厘米，2r×r÷2×2＝10          2r2＝10            r2＝510÷2＝5（平方厘米）5π：5＝π：1答：大圆与小正方形的面积比是π：1．故选：C。【考点评析】解答本题关键是明确圆的面积和小正方形的面积与大正方形的面积之间的关系．【举一反三02】（2020•长沙）图中是一个边长为4厘米的正方形，那么总的阴影面积是多少平方厘米？（π取3.14）【思路点拨】沿上图割补，阴影部分的面积＝半圆的面积+正方形面积的四分之一，根据正方形的面积公式S＝a2，和圆的面积公式S＝πr2解答即可。【规范解答】解：4÷2＝2（厘米）3.14×22÷2+4×4÷4＝6.28+4＝10.28（平方厘米）答：总的阴影面积是10.28平方厘米。【考点评析】在求不规则图形面积时，往往利用割补结合：观察图形，把图形分割，再进行移补，形成一个容易求得的图形进行解答。【举一反三03】（2020•雨花区）草原上有一等边三角形建筑物边长是6米，一只羊被拴在建筑物的一个角上.已知绳子长8米，这只羊能吃到草的总面积是多少平方米？（π取3.14，结果精确到小数点后一位）【思路点拨】根据题意可知，羊可以吃到草的面积是以8米为半径、圆心角为：360°﹣60°＝300°的扇形的面积，加上2个半径是：8﹣6＝2（米）、圆心角是180°﹣60°＝120°的扇形面积的和。利用扇形面积公式计算即可。【规范解答】解：如图：360°﹣60°＝300°180°﹣60°＝120°×3.14×82+×3.14×（8﹣6）2×2＝×3.14+×3.14＝56×3.14≈175.8（平方米）答：这只羊能吃到草的总面积是175.8平方米。【考点评析】本题主要考查组合图形的面积，关键是利用扇形面积公式计算。高频考点02：用正方体搭立体图形【典例精讲02】（2022•米脂县）用长20cm、宽15cm、高6cm的长方体木块堆成一个正方体，至少需要（　　）块这样的长方体木块。A．30 B．60 C．90 D．120【思路点拨】首先要求出堆成的正方体的棱长是多少厘米，也就是要求出20、15、6的最小公倍数，这个数就是堆成的正方体的棱长；再分别用棱长除以原来的长、宽、高，求出长着要堆几块，宽着要堆几块，高着要堆几块，最后用这三个块数相乘就得需要的总块数。【规范解答】解：20＝2×2×515＝3×56＝2×320、15和6的最小公倍数是5×2×3×2＝60堆成的正方体的棱长是60厘米60÷20＝3（块）60÷15＝4（块）60÷6＝10（块）3×4×10＝120（块）答：至少需要120块这样的木块。故选：D。【考点评析】此题主要考查三个数的最小公倍数的求法，以及正方体体积的求法，用三个数公有的质因数、每两个数公有的质因数、每个数独有的质因数连乘所得的积就是三个数的最小公倍数，用长着摆的块数乘宽着摆的块数乘高着摆的块数就得总块数。【举一反三04】（2016•焦作）由几个相同的小正方体搭成的几何体的视图如图所示，则搭成这个几何体的小正方体的个数至少是　9　个．【思路点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形，依此分别得到第一层有6个正方体，第二层有2个正方体，第三层有1个正方体，相加即可求解．【规范解答】解：由以上分析得，第一层有6个正方体，第二层至少有2个正方体，第三层有1个正方体，所以至少共有6+2+1＝9个．故答案为：9．【考点评析】考查从不同方向观察物体和几何体，要求学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．【举一反三05】从上面和前面都看到了如图的图形，这个图形是由若干个棱长为1厘米的小正方体木块搭成的，搭成这个图形最多需要　9　个这样的小正方体．搭成的这个图形的最大表面积是　28平方厘米　．【思路点拨】从前面看有两层，上层2个，下层3个；从上面看有3排第一、二排各有2个，第三排有1个；所以拼成了棱长为2厘米的大正方体并且在前排紧挨着一个小正方体，由此可得搭成这个图形最多需要9个这样的小正方体，进而可求出搭成的这个图形的最大表面积是多少．【规范解答】解：搭成这个图形最多需要9个这样的小正方体．把小正方体的右侧面补到与大正方体重合的地方，搭成的这个图形的最大表面积是：2×2×6+1×1×4，＝24+4，＝28（平方厘米）；答：搭成这个图形最多需要9个这样的小正方体； 搭成的这个图形的最大表面积是28平方厘米．故答案为：9，28平方厘米．【考点评析】本题考查了从不同方向观察几何体，需要学生在观察时注意每个面有几排，每排有几个，每排的形状是什么样．【举一反三06】（2022•白河县）一个立体图形，从上面和正面看到的形状都是，搭建这样的立体图形至少需要5个小正方体。 　×　（判断对错）【思路点拨】这个立方体图形，从正面看是3个正方形，说明从正面看是由3个小正方体组成的，分两层，下层2个，上层1个居右；从上面看也是3个正方形，由3个正方体组成，分两行，前面一行有3个，这3个就是从正面看到的这3个小正方体，后面一行最少有1个，最多有2个，据此解答。【规范解答】解：从上面和正面看到的形状都是如图，搭成这样的立体图形前排3个小正方体，后排靠左边最少有1个，最多有2个。最少需要3+1＝4（个）最多需要3+2＝5（个）故答案为：×。【考点评析】本题是从不同方向观察物体和几何体，意在训练学生观察能力和分析判断能力。高频考点03：组合图形的面积【典例精讲03】（2023•宿迁模拟）如图中，甲的面积与乙的面积相比较，（　　）A．甲的面积大 B．乙的面积大 C．甲、乙面积相等【思路点拨】甲和乙的面积都等于以梯形的上底为底，以梯形的高为高的三角形的面积减去上面空白三角形的面积。据此分析即可。【规范解答】解：甲和乙的面积都等于以梯形的上底为底，以梯形的高为高的三角形的面积减去上面空白三角形的面积，所以甲和乙的面积相等。故选：C。【考点评析】此题考查了学生的观察能力和分析能力。【举一反三07】（2023•铁山区模拟）如图，两个涂色的小正方形周长之和是4分米。大正方形的面积是多少平方分米？【思路点拨】根据两个涂色的小正方形周长之和是4分米，可求出两个小正方形的边长和是（4÷4）分米，即大正方形的边长，再根据正方形的面积公式S＝a2即可求解。【规范解答】解：两个正方形的边长和为：4÷4＝1（分米），即大正方形的边长为1分米，所以大正方形的面积为：1×1＝1（平方分米）答：大正方形的面积是1平方分米。【考点评析】本题主要考查了组合图形的面积，解题的关键是确定两个正方形的边长和，即大正方形的边长。【举一反三08】（2022•高台县模拟）求图中阴影部分的面积。 【思路点拨】用上底60分米、下底80分米、高30分米的梯形的面积减去底60分米、高20分米的三角形的面积即可。【规范解答】解：（60+80）×30÷2﹣60×20÷2＝2100﹣600＝1500 （平方分米）答：阴影部分的面积是1500平方分米。【考点评析】解答本题的关键是熟练掌握梯形和三角形的面积公式。【举一反三09】（2022•揭东区模拟）求阴影部分的面积。【思路点拨】（1）阴影部分是两个相同的三角形，三角形的底5分米，高6分米，利用 S＝ah 计算即可。（2）阴影部分是一个下底为大正方形边长6分米，上底和高为小正方形边长4分米的梯形，根据 S＝（a+b）h 计算即可。【规范解答】解：（1）×5×6×2＝5×6＝30（平方分米）（2）×（4+6）×4＝×10×4＝20（平方分米）【考点评析】本题考查了组合图形的面积，识图能力是关键。高频考点04：组合图形的体积【典例精讲04】（2022•管城区）蒙古包由一个近似的圆柱和一个近似的圆锥组成。圆柱部分的底面直径是8米，高是2米，圆锥部分的高是1.2米，这个蒙古包的容积大约是多少立方米？（蒙古包的厚度不计）【思路点拨】根据圆锥的体积公式：V＝πr2h，圆柱的体积公式：V＝πr2h，把数据代入公式求出圆锥与圆柱的体积和即可。【规范解答】解：3.14×（8÷2）2×1.2+3.14×（8÷2）2×2＝×3.14×16×1.2+3.14×16×2＝20.096+100.48＝120.576（立方米）答：这个蒙古包的容积大约是120.576立方米。【考点评析】此题主要考查圆锥、圆柱体积公式的灵活运用，关键是熟记公式。【举一反三10】（2022•建华区）有一块正方体的木料，它的棱长是5dm。把这块木料加工成一个最大的圆柱（如图所示）。体积减少了多少立方分米？【思路点拨】通过观察图形可知，把这个正方体木料加工成一个最大的圆柱，这个圆柱的底面直径和高都等于正方体的棱长，减少部分的体积等于正方体的体积与圆柱的体积差。根据正方体的体积公式：V＝a3圆柱的体积公式：V＝πr2h，把数据代入公式解答。【规范解答】解：5×5×5﹣3.14×（5÷2）2×5＝25×5﹣3.14×6.25×5＝125﹣19.625×5＝125﹣98.125＝26.875（立方分米）答：体积减少了26.875立方分米。【考点评析】此题主要考查正方体的体积公式、圆柱的体积公式的灵活运用，关键是熟记公式。【举一反三11】（2022•中原区）安安自制了一个污水过滤器进行污水过滤实验，如图所示。将污水倒入上方的近似圆锥形容器内，经过过滤管的过滤后，清水滴入下方的圆柱形容器（与圆锥形容器底面相同）。这个圆锥形容器一次能装入多少毫升的污水？如果这些污水全部过滤到如图圆柱形容器中，水的高度是多少？（不考虑过滤掉的杂质的体积）【思路点拨】根据圆锥的容积公式：V＝πr2h，把数据代入公式求出圆锥容器的容积；因为等底等高的圆柱的体积是圆锥体积的3倍，所以当圆柱与圆锥的体积相等，底面积也相等时，圆柱的高是圆锥高的，据此解答即可。【规范解答】解：×3.14×（10÷2）2×9＝×3.14×25×9＝235.5（立方厘米）235.5立方厘米＝235.5毫升9×＝3（厘米）答：这个圆锥形容器一次能装入235.5毫升的污水，圆柱容器内水的高是3厘米。【考点评析】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。【举一反三12】（2022•英德市）2021年4月22日，习近平总书记在北京以视频方式出席世界“领导人气候峰会”，他在讲话中指出：“以能源绿色低碳发展为关键，坚持走生态优先、绿色低碳的发展道路。”淘气准备制作一个低碳节能立体标志（如图，单位：厘米）。这个节能标志的体积是多少？【思路点拨】根据长方体的体积公式：V＝abh，圆柱的体积公式：V＝πr2h，把数据代入公式求出它们的体积差即可。【规范解答】解：6×2×4﹣3.14×（2÷2）2×2＝12×4﹣3.14×1×2＝48﹣6.28＝41.72（立方厘米）答：它的体积是41.72立方厘米。【考点评析】此题主要考查长方体的体积公式、圆柱的体积公式的灵活运用，关键是熟记公式一．选择题1．（2022•北辰区）如图在两个同样大小的正方形中阴影部分的面积相比（　　）A．A大 B．B大 C．一样大 D．无法比较【思路点拨】通过观察图形可知，两个图形中阴影部分的面积都是用正方形的面积减去4个完全一样的扇形（一个圆）的面积，如果两个正方形的面积相等，那么两个图形中阴影部分的面积就相等，如果两个正方形的不相等，那么正方形面积大的阴影部分的面积就大。据此解答。【规范解答】解：因为两个正方形的面积相等，A、B两个图形中阴影部分的面积都是用正方形的面积减去4个扇形（一个圆）的面积，所以阴影部分的面积一样大。故选：C。【考点评析】此题主要考查正方形面积公式、圆的面积公式的灵活运用，关键是熟记公式。2．（2022•揭东区）下列图形中，空白部分与阴影部分的周长相等，但面积不相等的图形是（　　）A． B． C． D．【思路点拨】根据周长、面积的意义，图A空白部分与阴影的周长相等，面积也相等；图B空白部分的周长与阴影部分的周长相等，面积不相等；图C空白部分的周长与阴影部分的周长，面积也相等；图D空白部分的周长与阴影部分的周长不相等，面积也不相等。据此解答。【规范解答】解：图A空白部分与阴影的周长相等，面积也相等；图B空白部分的周长与阴影部分的周长相等，面积不相等；图C空白部分的周长与阴影部分的周长，面积也相等；图D空白部分的周长与阴影部分的周长不相等，面积也不相等。故选：B。【考点评析】此题考查的目的是理解掌握圆、正方形、三角形、梯形周长、面积的意义及应用。3．（2022•吴中区）一个梯形如图，已知阴影部分的面积是12平方厘米，则梯形的面积是（　　）平方厘米。A．16 B．18 C．20 D．28【思路点拨】根据三角形的面积公式：S＝ah÷2，那么h＝2S÷a，把数据代入公式求出阴影部分三角形的高（梯形的高），再根据梯形的面积公式：S＝（a+b）h÷2，把数据代入公式解答。【规范解答】解：12×2÷6＝24÷6＝4（厘米）（8+6）×4÷2＝14×4÷2＝28（平方厘米）答：梯形的面积是28平方厘米。故选：D。【考点评析】此题主要考查三角形、梯形面积公式的灵活运用，关键是熟记公式，重点是求出三角形（梯形）的高。4．（2022•涵江区）在如图中平行四边形的面积是20cm2，图中阴影部分的面积是（　　）平方厘米。A．4 B．6 C．8 D．10【思路点拨】由平行四边形的面积是20cm2，可得一半的面积为20÷2＝10（cm2），根据等高三角形的面积比等于底边的比，可得阴影部分的面积占平行四边形一半的，根据分数乘法意义即可求出阴影部分的面积。【规范解答】解：20÷2×＝10×＝4（平方厘米）答：阴影部分的面积是4平方厘米。故选：A。【考点评析】本题主要考查了组合图形的面积，解题的关键是明确等高三角形的面积比等于底边的比。5．（2022•韩城市）图中阴影部分的面积是（　　）cm2。A．64 B．50.24 C．32 D．25.12【思路点拨】通过观察图形可知，把阴影部分通过“旋转”拼成一个三角形的面积，即阴影部分的面积等于正方形面积的一半，根据正方形的面积公式：S＝a2，把数据代入公式解答。【规范解答】解：如图： 8×8÷2＝64÷2＝32（平方厘米）答：阴影部分的面积是32平方厘米。故选：C。【考点评析】解答求不规则图形的面积，关键是通过“转化”，把不规则图形转化为规则图形进行解答。二．填空题6．（2022•洋县）如图中正方形B的面积是5cm2，那么图A的面积比正方形B大 　10.7　cm2。【思路点拨】利用圆的面积公式：S＝πr2，正方形面积公式：S＝a2，分别求出圆和正方形的面积，求差即可。【规范解答】解：3.14×5﹣5＝15.7﹣5＝10.7（平方厘米）答：图A的面积比正方形B大10.7平方厘米。故答案为：10.7。【考点评析】此题主要考查圆的面积公式、正方形的面积公式的灵活运用，关键是熟记公式。7．（2022•泾阳县）如图，阴影部分的周长是 　12.56　cm，面积是 　3.44　cm2。【思路点拨】通过观察图形，阴影部分的周长等于半径是（4÷2）厘米的圆的周长，阴影部分的面积等于正方形的面积减去圆的面积，根据圆的周长公式：C＝πd，圆的面积公式：S＝πr2，正方形的面积公式：S＝a2，把数据代入公式解答。【规范解答】解：3.14×4＝12.56（厘米）4×4﹣3.14×（4÷2）2＝16﹣3.14×4＝16﹣12.56＝3.44（平方厘米）答：阴影部分的周长是12.56厘米，面积是3.44平方厘米。故答案为：12.56，3.44。【考点评析】此题主要考查圆的周长公式、圆的面积公式、正方形的面积公式的灵活运用，关键是熟记公式。8．（2022•香洲区）如图中正方形的面积是40cm2，那么涂色部分的面积是 　94.2　cm2。【思路点拨】通过观察图形可知，正方形的边长等于圆的半径，涂色部分的面积是圆面积的四分之三，根据圆的面积公式：S＝πr2，把数据代入公式解答。【规范解答】解：3.14×40÷4×3＝125.6÷4×3＝31.4×3＝94.2（平方厘米）答：涂色部分的面积是94.2平方厘米。故答案为：94.2。【考点评析】此题主要考查正方形的面积公式、圆的面积公式的灵活运用，关键是熟记公式。9．（2022•渝北区模拟）如图是某糖厂制蔗糖后剩下的一堆甘蔗渣，糖厂运走这堆渣子的上半部分（圆锥形部分），运了15车。那么运剩下的部分（圆柱形部分）大约要运 　45　车。【思路点拨】因为等底等高的圆柱的体积是圆锥体积的倍，所以运走圆柱部分的车数是圆锥部分车数的3倍，据此解答即可。【规范解答】解：15×3＝45（车）答：运剩下的部分大约要运45车。故答案为：45。【考点评析】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及运用。10．（2022•凉山州）如图中有大小两个等腰直角三角形，已知阴影部分的面积是50cm2，环形的面积是 　157平方厘米　。【思路点拨】根据图形可知，大三角形的面积等于大圆的直径乘大圆的半径除以2，小三角形的面积等于小圆的直径乘小圆的半径除以2，阴影部分的面积等于大三角形的面积减小三角形的面积，等于大圆半径的平方减小圆半径的平方，圆环的面积等于大圆的面积减小圆的面积，据此解答即可。【规范解答】解：设大圆的半径为R，小圆的半径为r。50＝2R×R÷2﹣2r×r÷250＝R2﹣r2环形的面积是：3.14×R2﹣3.14×r2＝3.14×（R2﹣r2）＝3.14×50＝157（平方厘米）所以环形的面积是157平方厘米。故答案为：157平方厘米。【考点评析】解答此题的关键是分析出阴影部分的面积与圆环面积之间的关系。11．（2022•福清市）如图中，大圆直径是小圆直径的2倍，阴影部分的面积是18cm2，那么圆环的面积是 　56.52　cm2。【思路点拨】设小圆的半径为r，大圆的半径为R，根据阴影部分的面积是18cm2，可求出r2＝18÷3＝6（cm2），R2＝18+18÷3＝24（cm2），再根据圆环的面积＝3.14×（R2﹣r2），代入数据求解即可。【规范解答】解：3.14×（18+18÷3﹣18÷3）＝3.14×18＝56.52（cm2）答：圆环的面积是56.52cm2。【考点评析】本题主要考查了组合图形的面积，解题的关键是求出小圆半径的平方和大圆半径的平方。三．判断题12．（2021•西乡县）长方形、正方形和圆的周长相等，那么圆的面积一定最大．　√　．（判断对错）【思路点拨】周长相等时，形状越近似于圆，面积越大，反之，面积相等，形状越不接近圆，周长越大．【规范解答】解：长方形、正方形和圆的周长为12.56厘米；长方形的长宽可以为3.13厘米、3.15厘米，长方形的面积＝3.13×3.15＝9.8595（平方厘米）；正方形的边长为3.14厘米，正方形的面积＝3.14×3.14＝9.8596（平方厘米）；圆的面积＝3.14×（12.56÷3.14÷2）2＝12.56（平方厘米）；从上面可以看出圆的面积最大，由此我们可以得出一般结论：周长相等的长方形、正方形和圆，面积最大的是圆．故答案为：√．【考点评析】我们可以把周长相等的长方形、正方形和圆，面积最大的是圆当做一个正确的结论记住，快速去做一些选择题或判断题．13．（2015•如皋市模拟）一个正方形和一个圆的周长相等，圆面积一定大于正方形面积．　√　．（判断对错）【思路点拨】要比较周长相等的正方形和圆形，谁的面积最大，谁面积最小，可以先假设这两种图形的周长是多少，再利用这二种图形的面积公式，分别计算出它们的面积，最后比较这二种图形面积的大小．【规范解答】解：假设圆和正方形形的周长都是16，则圆的半径为：16÷π÷2＝，面积为：π××＝≈20.38，正方形的边长为：16÷4＝4，面积为：4×4＝16；所以圆的面积大于正方形的面积．故答案为：√．【考点评析】此题主要考查正方形、圆形的面积公式及灵活运用，解答此题可以先假设这图形的周长是多少，再利用图形的面积公式，分别计算出它们的面积，最后比较面积的大小．14．（2013•武鸣县模拟）一个圆的周长和一个正方形的周长相等，那么这个圆的面积大于正方形的面积．　√　．（判断对错）【思路点拨】这道题中圆和正方形的周长没有说明具体是多少，要比较它们的面积不好比较，因此，可以把它们的周长假设成一个数，根据“a＝c÷4和r＝c÷2π”算出正方形的边长和圆的半径，再根据正方形的面积公式和圆的面积公式，算出它们的面积后去比较大小，最后得出答案．【规范解答】解：假设圆的周长和正方形的周长是12.56厘米，则 正方形的边长 a＝c÷4＝12.56÷4＝3.14（厘米），正方形的面积 S＝a2＝3.14×3.14＝9.8596（平方厘米）；圆的半径r＝C÷2π＝12.56÷（2×3.14）＝2（厘米），圆的面积 S＝πr2＝3.14×22＝12.56（平方厘米），12.56＞9.8596，则圆的面积大于正方形的面积．故答案为：√．【考点评析】像这样没有具体数字而要求比较大小的题目，可以采用“假设法”，也就是举例子，放到具体的环境中去比较．四．计算题15．（2022•汝州市）（1）求阴影部分的面积。（单位：厘米）（2）计算零件的体积。（单位：分米）【思路点拨】（1）用上底4厘米、下底6厘米、高（4+6）厘米的梯形面积，减去半径4厘米的圆面积的，再减去底和高都是6厘米的三角形面积即可。（2）用长2分米、宽2分米、高3分米的长方体体积加上底面直径2分米、高3分米的圆锥的体积即可。【规范解答】解：（1）（4+6）×（4+6）÷2﹣3.14×42×﹣6×6÷2＝50﹣12.56﹣18＝19.44（平方厘米）答：阴影部分的面积为19.44平方厘米。（2）2×2×3+3.14×（2÷2）2×3×＝12+3.14＝15.14（立方分米）答：零件的体积为15.14立方分米。【考点评析】解答本题的关键是准确分析图形的组成，熟练掌握梯形、三角形、圆面积公式及长方体和圆锥体体积公式。五．应用题16．（2022•玉州区）陀螺在我国最少有四、五千年的历史，是民间最早的娱乐工具之一。小刚有一个底面直径是6厘米的木制陀螺（如图），这个陀螺的体积是多少立方厘米？【思路点拨】根据圆柱的体积公式：V＝πr2h，圆锥的体积公式：V＝πr2h，把数据代入公式圆柱与圆锥的体积和即可。【规范解答】解：3.14×（6÷2）2×3+×3.14×（6÷2）2×3＝3.14×9×3+3.14×9×3＝84.78+28.26＝113.04（立方厘米）答：这个陀螺的体积是113.04立方厘米。【考点评析】此题主要考查圆柱、圆锥体积公式的灵活运用，关键是熟记公式。17．（2022•洛龙区）陀螺在我国最少有四、五千年的历史，是民间最早的娱乐工具之一。小刚有一个底面直径约是6cm的木制陀螺（如图），这个陀螺的体积大约是多少？【思路点拨】根据圆柱的体积公式：V＝πr2，圆锥的体积公式：V＝r2h，把数据代入公式求出它们的体积和即可。【规范解答】解：3.14×（6÷2）2×6+3.14×（6÷2）2×3＝3.14×9×6+3.14×9×3＝169.56+28.26＝197.82（立方厘米）答：这个陀螺的体积大约是197.82立方厘米。【考点评析】此题主要考查圆柱、圆锥体积公式的灵活运用，关键是熟记公式。18．（2022•二七区）如图所示，大、小两个正方形之间有一部分阴影，求阴影部分的面积是多少？【思路点拨】阴影部分的面积等于圆的面积减去小正方形的面积，圆的直径等于大正方形的边长，小正方形的对角线的长度等于大正方形的边长，把小正方形分成两个完全相同的三角形，根据圆的面积公式：S＝πr2，三角形的面积公式：S＝ah÷2，把数据代入公式解答．【规范解答】解：3.14×（6÷2）2﹣6×（6÷2）÷2×2＝3.14×9﹣6×3÷2×2＝28.26﹣18＝10.26（平方厘米），答：阴影部分的面积是10.26平方厘米．【考点评析】此题主要考查圆的面积公式、三角形的面积公式的灵活运用，关键是熟记公式．19．（2021•杭州）计算阴影部分的面积。【思路点拨】通过观察图形可知，阴影部分的面积等于梯形的面积减求圆面积的四分之一，根据梯形的面积公式：S＝（a+b）h÷2，圆的面积公式：S＝πr2，把数据代入公式解答。【规范解答】解：（6+12）×6÷2﹣3.14×62÷4＝18×6÷2﹣3.14×36÷4＝54﹣28.26＝25.74（平方厘米）答：阴影部分的面积是25.74平方厘米。【考点评析】此题主要考查梯形的面积公式、圆的面积公式的灵活运用，关键是熟记公式。20．（2021•宁县）此图四边形ABCD是平行四边形，BC长为12厘米，阴影部分的面积是 　36　平方厘米。【思路点拨】把左边的阴影部分旋转到右边，可得：阴影部分的面积＝平行四边形的一半，据此求解即可。【规范解答】解：如图：12×（12÷2）÷2＝12×6÷2＝36（平方厘米）答：阴影部分的面积是36平方厘米。故答案为：36。【考点评析】本题主要考查了组合图形的面积，解题的关键是把不规则图形的面积转化为规则图形的面积。21．（2020•宝应县）中国建筑中经常见到“外方内圆”和“外圆内方”的设计。如图中两个圆的直径都是4厘米，分别计算正方形和圆之间的部分各是多少平方厘米？【思路点拨】（1）由图示可知，圆的直径等于正方形的边长，正方形和圆之间的部分的面积等于正方形的面积减去圆的面积；（2）根据图示，把正方形分成两个等腰直角三角形，三角形的底等于圆的直径，三角形的高等于圆的半径。正方形和圆之间的部分的面积等于圆的面积减去正方形的面积。利用正方形面积公式：S＝a2，圆的面积公式：S＝πr2，三角形面积公式：S＝ah÷2，计算即可。【规范解答】解：（1）4×4﹣3.14×（4÷2）2＝16﹣12.56＝3.44（平方厘米）答：正方形和圆之间的部分的面积是3.44平方厘米。（2）3.14×（4÷2）2﹣4÷2×2×4÷2＝12.56﹣8＝4.56（平方厘米）答：正方形和圆之间的部分的面积是4.56平方厘米。【考点评析】本题属于求组合图形面积的问题，这种类型的题目主要明确组合图形是由哪些基本的图形构成的，然后看是求几种图形的面积和还是求面积差，然后根据面积公式解答即可。22．（2022•龙川县）计算阴影部分的面积。 【思路点拨】由图可知，阴影部分的面积等于半径（12+2）分米的圆面积的减去半径12分米的圆面积的。【规范解答】解：3.14×（12+2）2×﹣3.14×122×＝3.14×（196﹣144）×＝3.14×13＝40.82（平方分米）答：阴影部分的面积是40.82平方分米。【考点评析】解答本题需正确分析阴影部分的组成，熟练使用圆面积公式。23．（2022•成安县模拟）求如图组合图形的体积。【思路点拨】根据圆锥的体积公式：V＝sh，圆柱的体积公式：V＝sh，把数据分别代入公式求出它们的体积和即可。【规范解答】解：×3.14×（18.84÷3.14÷2）2×6+3.14×（18.84÷3.14÷2）2×4＝×3.14×9×6+3.14×9×4＝56.52+113.04＝169.56（立方厘米）答：它的体积是169.56立方厘米。【考点评析】此题主要考查圆柱、圆锥体积公式的灵活运用，关键是熟记公式。24．（2022•成安县模拟）求如图阴影部分的面积。【思路点拨】用上底12分米、下底15分米、高10分米的梯形面积减去直径10分米的圆面积的一半，即可求出阴影部分的面积。【规范解答】解：（12+15）×10÷2﹣3.14×（10÷2）2÷2＝135﹣39.25＝95.75（平方分米）答：阴影部分的面积是95.75平方分米。【考点评析】解答本题的关键是熟练掌握梯形面积和圆面积公式。25．（2022•崇左模拟）如图，公园要在一块梯形地里建一个圆形水池，其余的地方是草坪。草坪的面积是多少平方米？【思路点拨】用上底30米、下底70米、高40米的梯形面积减去直径4米的圆面积即可。【规范解答】解：（30+70）×40÷2﹣3.14×（4÷2）2＝2000﹣12.56＝1987.44（平方米）答：草坪的面积是1987.44平方米。【考点评析】解答本题需熟练掌握梯形及圆面积公式。26．（2022•未央区）下面是一个零件的示意图（单位：厘米），它是由一个长方体从前往后挖掉（挖通）一个底面直径为10厘米的圆柱体得到的，求这个零件的体积。（x取3.14）【思路点拨】通过观察图形可知，这个零件的体积等于长方体的体积减去圆柱的体积，根据长方体的体积公式：V＝abh，圆柱的体积公式：V＝πr2h，把数据代入公式解答。【规范解答】解：30×5×20﹣3.14×（10÷2）2×5＝150×20﹣3.14×25×5＝3000﹣392.5＝2607.5（立方厘米）答：这个零件的体积是2607.5立方厘米。【考点评析】此题主要考查长方体的体积公式、圆柱的体积公式的灵活运用，关键是熟记公式。27．（2022•太原模拟）求如图图形的体积。【思路点拨】用棱长4厘米的正方体的体积加上底面直径4厘米，高3厘米的圆锥体的体积即可。【规范解答】解：×3.14×（4÷2）2×3+4×4×4＝12.56+64＝76.56（立方厘米）【考点评析】本题考查了正方体和圆锥体的体积，需熟记公式，解答本题的关键是确定圆锥体的底面直径