题型二 填空题99题（一）——（2023专用）2022年全国各地区小升初数学真题题型汇编（通用版）（含解析）

这是一份题型二 填空题99题（一）——（2023专用）2022年全国各地区小升初数学真题题型汇编（通用版）（含解析），共23页。试卷主要包含了填空题等内容，欢迎下载使用。
小升初真题练：题型二 填空题99题（一）
（2023年专用）2022年全国各地区小升初真题题型汇编
亲爱的同学们，小升初的复习已经开始，特为大家准备了2022年全国各地区的小升初考试真题，尤其以常考易错真题为主，大家可以进行题型专项训练，提高成绩，做到举一反三！题型数量大，大家不用一次性做完，可以分批次进行，预祝大家成绩步步高升！
一、填空题
1．（2022·湖南衡阳·统考小升初真题）海平面的海拔记作0m，高出海平面850m，海拔为( )，低于海平面320m，海拔为( )。
2．（2022·湖南衡阳·统考小升初真题）一个数由9个亿、5个百万、4个十万、8个千组成，这个数写作( )，省略“亿”后面的尾数（保留整数）约是( )亿。
3．（2022·河南漯河·统考小升初真题）如果，那么x∶y＝( )∶( )。
4．（2022·河南漯河·统考小升初真题）比100米少25%是( )米，比8千克多千克是( )千克。
5．（2022·甘肃天水·统考小升初真题）甘肃省海拔最低处是陇南白龙江中游文县罐子沟，海拔是550米，记作﹢550米，中国海拔最低处是新疆艾丁湖，低于海平面154.21米，记作( )米。
6．（2022·河南漯河·统考小升初真题）2.05时＝( )时( )分        5吨28千克＝( )吨
7．（2022·湖南衡阳·统考小升初真题）一件衣服打八折出售，现价是原价的( )%。
8．（2022·湖南岳阳·统考小升初真题）1时45分＝( )时    3.5公顷＝( )平方米
9．（2022·湖南岳阳·统考小升初真题）“五一”假期，某景点共接待游客二百七十万六千人，写作( )人，改写成以“万”作单位的数是( )万人。
10．（2022·甘肃天水·统考小升初真题）有红、白、黄、绿、黑五种颜色的球各3个，至少摸( )个球，保证能够取得两个颜色相同的球。
11．（2022·浙江温州·统考小升初真题）据温州市水资源公报显示，2021年平均降水量2228.7mm，折合水量二百六十九亿四千万m3，横线上的数写作( )，改写成用“亿”作单位的数是( )亿m3。
12．（2022·甘肃天水·统考小升初真题）黄河小浪底景区为中原地区最具特色的风景之一，被评为“中国黄河50景”。小浪底工程坝址控制流域面积694200平方千米，694200改写成用“万”作单位的数是( )万；水库总库容12650000000立方米，12650000000省略亿位后面的尾数约是( )亿。
13．（2022·福建福州·统考小升初真题）“太阳升起东山头，鸭子嘎嘎走出窝；一半的一半水中游，剩下一半坡下走，窝内还剩18只，”根据这首歌谣可知，一共有( )只鸭子。
14．（2022·甘肃天水·统考小升初真题）0.6m3＝( )dm3    3时15分＝( )时
15．（2022·福建福州·统考小升初真题）乒乓球是中国国球，是一种世界流行的球类体育项目，比赛分团体、单打、双打等数种。标准的比赛用球（赛璐珞球）质量是每粒2.5±0.2g。某次抽检五粒球的质量分别是2.56g、2.61g、2.73g、2.58g和2.50g，这些乒乓球的合格率为( )%。
16．（2022·甘肃天水·统考小升初真题）如果A÷6＝B（A、B均为非0自然数），则A和B的最大公因数是( )；如果，那么x和y成( )比例。
17．（2022·福建福州·统考小升初真题）请你再添上一个数，让它能与3、、0.5组成比例，所组成的这个比例是( )。
18．（2022·河南漯河·统考小升初真题）下图是一个蛋糕盒，盒子上扎了一根漂亮的丝带，已知蛋糕底面周长是94.2cm，高是18cm，接头处用去了30cm，这根丝带长( )cm。

19．（2022·福建福州·统考小升初真题）一个圆柱和一个圆锥，底面周长之比是3∶2，它们的体积之比是5∶2，那么圆锥与圆柱高的比是( )。
20．（2022·河南漯河·统考小升初真题）一个长方形的周长是60cm，长和宽的比是3∶2，这个长方形的长是( )cm，面积是( )cm2。
21．（2022·福建福州·统考小升初真题）如图中，大圆直径是小圆直径的2倍，阴影部分的面积是，那么圆环的面积是( )。

22．（2022·广东茂名·统考小升初真题）一个圆柱体与和它等底的圆锥体的体积相等，圆锥体的高是12厘米，圆柱体的高是( ) 厘米。
23．（2022·甘肃天水·统考小升初真题）六年级一共有学生160人，参加兴趣小组的学生人数占六年级总人数的百分比如图所示，根据如图可以算出六年级参加书法组的有( )人。

24．（2022·福建福州·统考小升初真题）新疆不仅风光旖旎，而且物产丰裕。在崇山峻岭、绿洲戈壁之间，有着数不尽的“粮仓”“肉库”“油盆”“煤海”等、新疆名酒伊力特，瓶身上标示：酒精度52%，净含量500mL。这里的52%表示( )占( )的52%，这瓶酒中含水( )mL。
25．（2022·福建福州·统考小升初真题）用直角边为1厘米的等腰直角三角形，按照如下规律拼图形：

那么，拼成的第27个图形的周长是( )厘米。
26．（2022·湖南岳阳·统考小升初真题）如图，把长方形以AB为轴旋转一周可以得到一个圆柱，这个圆柱的体积是( )立方厘米，把它削成一个最大的圆锥，削去了( )立方厘米。

27．（2022·湖南衡阳·统考小升初真题）把0.25∶化成最简单整数比是( )，比值是( )。
28．（2022·福建福州·统考小升初真题）（    ）∶10＝＝5÷（    ）＝＝（    ）折。
29．（2022·河南漯河·统考小升初真题）在一次不到50人的书法比赛中，有的人获得一等奖，有的人获得二等奖，有的人获得三等奖，其余获得优胜奖，获得优胜奖的有( )人。
30．（2022·湖南岳阳·统考小升初真题）把甲图形按一定比例缩小成为乙图形，则x＝( )。

31．（2022·浙江温州·统考小升初真题）吃粽子是端午节的一项传统习俗，某店粽子线上和线下销的比是5∶2，如果销售总量是6300个，那么线上销量是( )个，线上销量比线下销量多( )%。
32．（2022·福建福州·统考小升初真题）根据下图列出乘法算式( )。

33．（2022·山东济南·统考小升初真题）＝80%＝（    ）成。
34．（2022·湖南岳阳·统考小升初真题）盒子里有同样大小的红球5个，黄球7个，白球6个，摸到( )球可能性最大，要想摸出的球一定有三种颜色，至少要摸出( )个球。
35．（2022·山东济南·统考小升初真题）下面是一个直角三角形，如果以a边为轴旋转一周，将形成一个( )，这个立体图形的高是( )，b是它的( )，它的底面周长是( )。

36．（2022·浙江温州·统考小升初真题）“全城志愿”正成为鹿城文明新风尚，某志愿小队有25名队员，那么他们中至少有( )人是同一个月出生的。在他们中选择5人担任小组长，那么至少有( )人的性别是相同的。
37．（2022·山东济南·统考小升初真题）有3cm、8cm的小棒各两根，选其中三根围成一个等腰三角形，它的周长是( )cm。
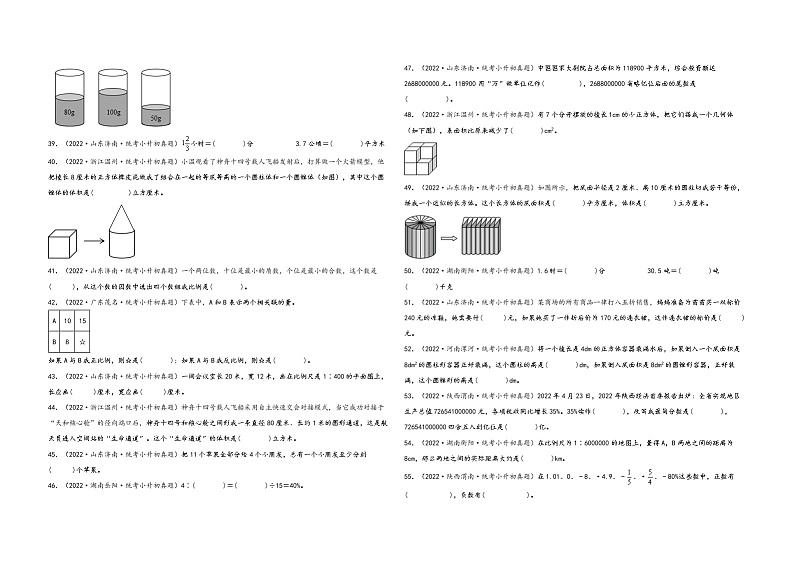
38．（2022·湖南岳阳·统考小升初真题）如图的三杯水中分别放入5g糖。其中最甜的一杯，糖占糖水的( )。

39．（2022·山东济南·统考小升初真题）小时＝( )分      3.7公顷＝( )平方米
40．（2022·浙江温州·统考小升初真题）小温观看了神舟十四号载人飞船发射后，打算做一个火箭模型，他把棱长8厘米的正方体橡皮泥做成了组合在一起的等底等高的一个圆柱体和一个圆锥体（如图），其中这个圆锥体的体积是( )立方厘米。

41．（2022·山东济南·统考小升初真题）一个两位数，十位是最小的质数，个位是最小的合数，这个数是( )，从这个数的因数中选出四个数组成比例是( )。
42．（2022·广东茂名·统考小升初真题）下表中，A和B表示两个相关联的量。
A
10
15
B
8
☆
如果A与B成正比例，则☆是( )；如果A与B成反比例，则☆是( )。
43．（2022·山东济南·统考小升初真题）一间会议室长20米，宽12米，画在比例尺是1∶400的平面图上，长应画( )厘米，宽应画( )厘米。
44．（2022·浙江温州·统考小升初真题）神舟十四号载人飞船采用自主快速交会对接模式，当它成功对接于“天和核心舱”的径向端口后，神舟十四号和核心舱之间形成一条直径80厘米、长约1米的圆形通道，这是航天员进入空间站的“生命通道”。这个“生命通道”的体积是( )立方米。
45．（2022·山东济南·统考小升初真题）把11个苹果全部分给4个小朋友，总有一个小朋友至少分到( )个苹果。
46．（2022·湖南岳阳·统考小升初真题）4∶( )＝( )÷15＝40%。
47．（2022·山东济南·统考小升初真题）中国国家大剧院占总面积为118900平方米，综合投资额达2688000000元。118900用“万”做单位记作( )，2688000000省略亿位后面的尾数是( )。
48．（2022·浙江温州·统考小升初真题）有7个分开摆放的棱长1cm的小正方体，把它们搭成一个几何体（如下图），表面积比原来减少了( )cm2。

49．（2022·山东济南·统考小升初真题）如图所示，把底面半径是2厘米、高10厘米的圆柱切成若干等份，拼成一个近似的长方体。这个长方体的底面积是( )平方厘米，体积是( )立方厘米。

50．（2022·湖南衡阳·统考小升初真题）1.6时＝( )分      30.5吨＝( )吨( )千克
51．（2022·山东济南·统考小升初真题）某商场的所有商品一律打八五折销售，妈妈准备为苗苗买一双标价240元的凉鞋，她需要付( )元，如果她买了一件折后价为170元的连衣裙，这件连衣裙的标价是( )元。
52．（2022·河南漯河·统考小升初真题）将一个棱长是4dm的正方体容器装满水后，如果倒入一个底面积是8dm2的圆柱形容器正好装满，这个圆柱的高是( )dm，如果倒入底面积是8dm2的圆锥形容器，正好装满，这个圆锥形的高是( )dm。
53．（2022·陕西渭南·统考小升初真题）2022年4月23日，2022年陕西经济首季报告出炉：全省实现地区生产总值726541000000元，各项税收同比增长35%。35%读作( )，改写成最简分数是( )，726541000000四舍五入到亿位是( )亿。
54．（2022·湖南衡阳·统考小升初真题）在比例尺为1∶6000000的地图上，量得A，B两地之间的距离为8cm，那么两地之间的实际距离大约是( )km。
55．（2022·陕西渭南·统考小升初真题）在1.01、0、﹣8、﹢4.9、﹣、﹢、﹣80%这些数中，正数有( )，负数有( )。
56．（2022·浙江温州·统考小升初真题）火箭模型中一个圆柱形零件的高是5mm，在图纸上的高是3cm。这幅图纸的比例尺是( )。
57．（2022·陕西渭南·统考小升初真题）一座高12米的小山丘，画在图上高6厘米，这幅图的比例尺是( )；这幅图上长15厘米的公路，实际长是( )米。
58．（2022·湖南衡阳·统考小升初真题）若a∶b＝1∶2，a∶c＝1∶3则a∶b∶c＝( )。
59．（2022·陕西渭南·统考小升初真题）为响应“双减”政策，提升学生的艺体素养，某校计划开设武术、舞蹈、剪纸等三项活动课程，随机抽取了部分学生，统计他们喜欢的课程（每人只能从中选一项），并将统计结果绘制成如下统计图，看图回答问题。

(1)选择剪纸的有( )名学生，选择武术的学生比选择舞蹈的多( )人。
(2)平均选择每个活动课程的有( )人，选择剪纸的人数比选择武术的少( )%。
60．（2022·浙江温州·统考小升初真题）钟面上长度为8cm的分针，经过一小时，它扫过的面积是( )cm2，它的针尖经过的路程是( )cm。
61．（2022·陕西渭南·统考小升初真题）有甲、乙两筐草莓，乙筐装有1.44千克草莓，如果从甲筐倒出20%给乙筐，则两筐一样重，甲筐原有( )千克草莓。
62．（2022·湖南衡阳·统考小升初真题）老师把6米长的铁丝平均锯成7段，每段长( )米，每段是这根铁丝的( )。
63．（2022·陕西渭南·统考小升初真题）一个圆锥的底面周长是31.4cm，高是6cm，它的体积是( )。
64．（2022·浙江温州·统考小升初真题）一根绳子长5m，先剪去它的，又剪去m，还剩下( )m。
65．（2022·陕西渭南·统考小升初真题）每年4月23日是世界读书日，高尔基说：“书，是人类进步的阶梯”，阅读可以启智增慧，拓展视野，2022年世界读书日来临之际，某校为了解学生阅读情况，对部分学生每天的阅读总时间进行了随机抽样调查，被抽样的每名学生每天阅读的总时间分为四个类别：A：不超过1小时，B：超过1小时但不超过2小时，C：超过2小时但不超过4小时，D：超过4小时，将分类结果制成如下的扇形统计图。已知选择B的有66名学生，则一共抽查了( )名学生，选择D的比选择C的多( )名学生。

66．（2022·湖南衡阳·统考小升初真题）比80米多的是( )米；12千克比15千克少( )%。
67．（2022·陕西渭南·统考小升初真题）已知（a和b都是不为0的自然数），a和b成( )（填“正”或“反”）比例，ab－25＝( )。
68．（2022·河南漯河·统考小升初真题）一件商品原价2000元，现打七五折销售，比原来便宜( )元。
69．（2022·陕西渭南·统考小升初真题）如图是一组有规律的图案，第1个图案中有8个小正方形，第2个图案中有12个小正方形，第3个图案中有16个小正方形，……，依此规律，第14个图中有( )个小正方形，若第n个图案中有240个小正方形，则n的值为( )。

70．（2022·河南漯河·统考小升初真题）如图，红花种植面积占圆形花池面积的，占长方形花池面积的。种植的黄花与粉花的面积比是　 　。

71．（2022·山西太原·校考小升初真题）一个圆柱削去12立方分米，正好削成了一个与它等底等高的圆锥，这个圆柱的体积是( )立方分米，圆锥的体积是( )立方分米。
72．（2022·甘肃天水·统考小升初真题）一个无盖长方体玻璃鱼缸长8分米，宽4分米，高6分米，制作这个鱼缸至少需要玻璃( )平方分米，这个鱼缸（玻璃厚度不计）装满水约是( )升，将这些水全部倒入底面积为24平方分米的圆柱形容器里（水没有溢出），水面高度是( )分米。
73．（2022·山西太原·校考小升初真题）( )12∶( )＝( )%＝( )小数。
74．（2022·甘肃天水·统考小升初真题）2022年6月5日神舟十四号载人飞船成功发射，陈冬、刘洋、蔡旭哲3名航天员领命出征，即将开启为期6个月的飞行任务。如图是一个正方体的展开图，将它折叠成正方体后，与“神”字相对面上的字是什么字？在正确答案下面画“√”。

14      成      功      发      射
（    ）  （    ）  （    ）  （    ）  （    ）
75．（2022·山东济南·小升初真题）截至2022年6月7日，我国累计报告接种疫苗为三十三亿八千五百八十五万次，横线上的数写作( )，省略亿位后面的尾数约是( )亿。
76．（2022·山西太原·校考小升初真题）2022年4月25日、26日，山西1632名援沪医疗队员从太原出发，奔赴上海疫情防控一线，“晋”心守“沪”！已知在比例尺1∶50000000的地图上，量得太原到上海的距离为2.7厘米，太原到上海的实际距离约为( )千米。
77．（2022·山西太原·校考小升初真题）《中华人民共和国国旗法》规定：国旗长和宽的比是3∶2，国旗的通用尺寸为五种，各界酌情选用。1号国旗长288cm，宽( )cm；4号国旗长( )cm，宽96cm。
78．（2022·湖南衡阳·统考小升初真题）( )∶5＝( )%＝＝18÷( )＝( )折。
79．（2022·山西太原·校考小升初真题）在一个比例中，两个内项的积是最小的质数，其中一个外项是，另一个外项是( )。
80．（2022·河南漯河·统考小升初真题）一种药水是用药粉和水按1∶200配制成的，现有药粉12千克，需要加水( )千克，配制成了药水是( )千克。
81．（2022·山西太原·校考小升初真题）45公顷＝( )平方千米            0.15时＝( )分
6千克30克＝( )千克                4500立方厘米＝( )升
82．（2022·山东济南·小升初真题）判断下面各题中两种相关联的量所成的比例关系。
(1)比例尺一定，图上距离与实际距离。成( )比例关系。
(2)购买物品的总价一定，购买的数量和单价。成( )比例关系。
83．（2022·山西太原·校考小升初真题）悠悠过生日，爸爸送给他一个圆锥形的陀螺，陀螺的底面直径是4cm，高是2.7cm，这个陀螺的体积是( )cm3；如果用一个长方体盒子包装它，这个盒子的容积至少是( )cm3。
84．（2022·山东济南·小升初真题）（    ）÷15＝0.4＝14∶（    ）＝＝（    ）%＝（    ）折。
85．（2022·山西太原·校考小升初真题）如图，悠悠用小棒摆六边形，摆1个六边形需要6根小棒，摆2个六边形需要11根小棒，照这样摆n个六边形需要( )根小棒；如果有56根小棒，可以摆( )个六边形。

86．（2022·山东济南·小升初真题）一列高铁在济南西站上车的乘客是62名，记作﹢62名，下车的乘客是94名，记作( )名，此时高铁上的人数比原来( )。（填多或少）
87．（2022·山西太原·校考小升初真题）如图，阴影部分的面积是62.8平方厘米，那么正方形的面积是( )平方厘米。

88．（2022·山东济南·小升初真题）观察如图，想一想。

第7幅图有( )个点子，第n幅图的点子总数是( )个。
89．（2022·山西太原·校考小升初真题）2022年2月4日至2022年2月20日北京举办了第24届冬奥会，成为历史上首个“双奥之城”。冬奥黑科技，向世界展示中国智慧，请你选择合适的数填空。
﹣8.5            6.2            350            90            50%
(1)“双奥场馆”国家游泳中心占地面积( )公顷，通过“水冰转换”成为冬奥会历史上最大体量的冰壶场馆，冰壶赛道冰面温度仅有( )℃，冰面以上1.5米处温度保持在10℃，看台温度16℃至18℃，既满足了冰壶比赛环境的需要，又为观众营造了舒适的观赛环境。
(2)京张高铁是北京冬奥会专用通道，也是我国首条建成投用的5G智能高铁，实现了时速( )千米自动驾驶功能，具备车站自动发车、区间自动运行、到站自动停车、自动门控等先进功能。
(3)在冬奥会速滑比赛中，运动员速度可达到15—18米/秒，而我国研发的“猎豹”高速摄像系统技术标准能达到25米/秒，约等于时速( )千米，能灵活地捕捉速滑中的各种场面，让比赛更加公平公正。
(4)首都体育馆同时承办花样滑冰和短道速滑两个项目，项目组二氧化碳快速“造冰”技术打造“最快冰面”，综合节能达到( )以上，达到国际先进水平。
90．（2022·山东济南·小升初真题）做一批零件，师傅需要用8小时完成，徒弟需要用12小时才能完成，师傅合作，( )小时能完成。
91．（2022·广东茂名·统考小升初真题）截至北京时间2022年05月25日09时36分25秒全球各国（地区）新型冠状病毒感染确诊患者人数为528779944，省略亿位后面的尾数约为（    ）；美国确诊患者人数为85241016，将这个数改写成用“万”作单位的数为（    ），中国大陆为223488这个数读作（    ）。经过估算，中国大陆的确诊患者人数约为美国的。
92．（2022·山东济南·小升初真题）一个平行四边形和一个三角形等底等高，已知平行四边形的面积是42dm2，三角形的面积是( )dm2。
93．（2022·广东茂名·统考小升初真题）一条鲨鱼在海平面以下150米处，鲨鱼的位置可以表示为﹣150米。一艘潜艇在鲨鱼正下方400米处，那么潜艇的位置可以表示为( )米：潜艇和鲨鱼的位置比较，( )的位置更低一些。
94．（2022·山东济南·小升初真题）一个圆柱形笔筒的底面半径是4cm，高是10cm，它的侧面积是( )cm2。
95．（2022·广东茂名·统考小升初真题）36的因数有( )，从中选出四个数组成一个比值最小的比例：( )。
96．（2022·山东济南·小升初真题）在一幅1∶17000000的地图上，量得甲地到乙地的距离是3cm，则甲地和乙地的实际距离是( )km。
97．（2022·广东茂名·统考小升初真题）如图，将一个半径5厘米的圆形纸片平均分成若干份，剪开后拼成一个近似的长方形；拼成的近似长方形的周长是( )厘米，面积是( )平方厘米。

98．（2022·福建福州·统考小升初真题）六（1）班54个同学中，至少有( )人在同一个月过生日。
99．（2022·广东茂名·统考小升初真题）如下图所示，第1个图案中有2个正方形，第2个图案中有5个正方形，第3个图案中有8个正方形…，则第5个图案中有( )个正方形，第n个图案中有( )个正方形。


























参考答案
1．     ﹢850m     ﹣320m
【分析】此题主要用正负数来表示具有意义相反的两种量：选海平面为标准记为0，高于海平面为正，低于海平面为负，直接得出结论即可。
【详解】由分析可得：海平面的海拔记作0m，高出海平面850m，海拔为﹢850m，低于海平面320m，海拔为﹣320m。
【点睛】此题首先要知道以谁为标准，规定超出标准的为正，低于标准的为负，由此用正负数解答问题。
2．     905408000     9
【分析】9个亿是900000000，5个百万是5000000，4个十万是400000，8个千是8000，由9个亿、5个百万、4个十万、8个千组成的数是900000000＋5000000＋400000＋8000＝905408000；省略“亿”后面的尾数就是四舍五入到亿位，就是把亿位后的千万位上的数进行四舍五入，再在数的后面写上“亿”字。
【详解】根据分析得，这个数写作：905408000；
905408000≈9亿。
【点睛】本题主要考查整数的写法和求近似数，注意求近似数时要带计数单位。
3．     8     5
【分析】根据比例的基本性质可知，两内项之积等于两外项之积，可得5x＝8y，把5和x看作比例的两个外项，把8和y看作比例的两个内项，即可写出比例式。
【详解】根据分析得，如果，5x＝8y，
可写成比例式：x∶y＝8∶5。
【点睛】此题的解题关键是灵活运用比例的基本性质求解。
4．     75    
【分析】求比100米少25%的数是多少，用100－100×25%即可解答；求比8千克多千克是多少，用加法解答即可。
【详解】100－100×25%
＝100－25
＝75（米）
8＋＝（千克）
【点睛】本题考查求比一个数少百分之几的数是多少，明确单位“1”是解题的关键。
5．﹣154.21
【分析】通常把海平面的高度记作0，高出海平面记作“﹢”，低于海平面记作“﹣”。
【详解】由分析可知：
低于海平面154.21米，记作﹣154.21米。
【点睛】本题是考查正、负数的意义及其应用。
6．     2     3     5.028
【分析】根据1时＝60分，1吨＝1000千克，进行换算即可。
【详解】0.05×60＝3（分），2.05时＝2时3分；28÷1000＝0.028（吨），5吨28千克＝5.028吨
【点睛】单位大变小乘进率，单位小变大除以进率。
7．80
【分析】把这件衣服的原价看作单位“1”，打八折出售，即现价是原价的80%。
【详解】一件衣服打八折出售，现价是原价的80%。
【点睛】本题考查折扣问题，明确几折就是原价的十分之几，也就是百分之几十。
8．     1.75     35000
【分析】1时＝60分，1公顷＝10000平方米，把45分换算成时，用45除以进率60；把3.5公顷换算成平方米，用3.5乘进率10000，据此解答。
【详解】45÷60＝0.75
1＋0.75＝1.75
3.5×10000＝35000
【点睛】本题涉及到单位换算，将高级单位换算成低级单位，乘它们之间的进率；将低级单位换算成高级单位，除以它们之间的进率。
9．     2706000     270.6
【分析】按照多位数的写法：从右边起，每四个数位是一级，先看这个数有几级；如果这个数有两级，就先写万级，再写个级；哪一个数位上一个单位也没有，就在那个数位上写0。把整万的数改写成以“万”为单位的数，就是把万位后面的0去掉，同时在后面加一个“万”字。
【详解】二百七十万六千写作：2706000，改写成以“万”作单位的数是270.6万。
【点睛】解答本题的关键是掌握整数的写法，同时注意数的改写时要带单位。
10．6
【分析】要保证得到两个颜色相同的球，那就是至少要取出6个，才能保证一定得到两个颜色相同的球；假设第一个球是红球，第二个球是白球，第三个球是黄球，第四个是绿球、第五个是黑球，那再取任意一个球，只能是五种颜色中的一个，出现同色，用“颜色数＋1”即可。
【详解】5＋1＝6（个）
【点睛】此类题有规律可循，当要求的是至少取几个，出现同色的球时，只要用颜色数加1即可得出结论。
11．     26940000000     269.4
【分析】大数的写法：1.先写亿级，再写万级，最后写个级；2.哪个数位上一个单位也没有，就在那个数位上写0；非整亿的数改写成用“亿”作单位，在“亿”位的右下角点上小数点，去掉小数末尾的0，再加上一个“亿”字。
【详解】横线上的数写作26940000000，改写成用“亿”作单位的数是269.4亿m3。
【点睛】本题考查大数的写法，掌握大数的写法是解题的关键。
12．     69.42     127
【分析】非整万的数改写成用“万”作单位，在“万”位的右下角点上小数点，再去掉末尾的0，最后再加上一个“万”字即可；省略亿位后面的尾数，看千万位上的数字是否满5，然后根据四舍五入法求近似数即可。
【详解】694200＝69.42万，12650000000≈127亿
694200改写成用“万”作单位的数是69.42万；水库总库容12650000000立方米，12650000000省略亿位后面的尾数约是127亿。
【点睛】本题考查求近似数，熟练运用四舍五入法求近似数是解题的关键。
13．72
【分析】把这群鸭子的总数看作是单位“1”，一半的一半水中游，也就是的在水中，剩下坡下走，窝内还剩18只，由此可以求出18只占总数的几分之几，然后根据已知一个数的几分之几是多少，求这个数，用除法解答。
【详解】18÷（1－×－）
＝18÷（1－－）
＝18÷
＝72（只）
一共有72只鸭子。
【点睛】本题考查了分数除法的应用，解题的关键是正确找出单位“1”及18对应的分率。
14．     600     3.25
【分析】高级单位换低级单位乘进率，根据1m3＝1000dm3，用0.6×1000即可；低级单位换高级单位除以进率，根据1时＝60分，用15÷60再加上3时即可。
【详解】0.6m3＝0.6×1000dm3＝600dm3
3时15分＝3时＋15÷60时＝3时＋0.25时＝3.25时
【点睛】本题考查单位换算，明确各单位之间的进率是解题的关键。
15．80
【分析】正数、负数表示两种相反意义的量。“2.5±0.2g ”的含义，即2.5g是这种比赛用球的标准净重，实际每粒球的质量最多不超过（2.5＋0.2）g，最少不低于（2.5－0.2）g，比较抽检的五粒球的质量，质量在范围内的是合格的粒数，然后根据“合格率＝合格的粒数÷总粒数×100%”，代入数据计算即可。
【详解】最多不超过：2.5＋0.2＝2.7（g）
最少不低于：2.5－0.2＝2.3（g）
2.3g＜标准的比赛用球的质量＜2.7g
2.3＜2.56＜2.7，合格；
2.3＜2.61＜2.7，合格；
2.73＞2.7，不合格；
2.3＜2.58＜2.7，合格；
2.3＜2.50＜2.7，合格；
抽检的五粒球的质量有1粒不合格，4粒合格；
合格率为：
4÷5×100%
＝0.8×100%
＝80%
【点睛】本题考查正负数的意义及应用和百分率的计算，知道以哪个数为标准，规定超出标准的为正，低于标准的为负；明确求一个数是另一个数的百分之几，用除法计算。
16．     B     正
【分析】若两个数成倍数关系，它们的最大公因数就是较小的数；两个相关联的量，若它们的乘积一定，则它们成反比例；若它们的比值一定，则它们成正比例。
【详解】因为A÷6＝B，所以A÷B＝6，所以A和B的最大公因数是B；
因为，所以5x＝4y，即x∶y＝4∶5＝，x和y的比值一定，那么x和y成正比例。
【点睛】本题考查正反比例的判定，明确正反比例的定义是解题的关键。
17．3∶＝9∶0.5
【分析】若两组比的比值相等，则这两组比可以组成比例。
【详解】3÷＝18
18×0.5＝9
所组成的这个比例是3∶＝9∶0.5（答案不唯一）
【点睛】本题考查比例的意义，明确比例的意义是解题的关键。
18．414
【分析】由题意可知，根据圆的周长公式：C＝πd，据此可求出底面圆的直径，这根丝带的长度＝8条直径的长度＋8条高的长度＋接头处的长度，据此解答即可。
【详解】94.2÷3.14＝30（cm）
30×8＋8×18＋30
＝240＋144＋30
＝384＋30
＝414（cm）
【点睛】本题考查圆的周长，明确彩带都是由哪几部分构成的是解题的关键。
19．27∶10
【分析】根据底面周长的比是3∶2即半径的比是3∶2，把圆柱的半径看作3份，那圆锥的半径看作2份，根据体积比是5∶2，把圆柱的体积看作5份，那圆锥的体积看作2份，最后根据圆柱和圆锥的体积，即可求出，圆锥与圆柱高的比，再根据比的基本性质，化成最简单的整数比。
【详解】圆锥与圆柱高的最简单的整数比是：
[2×3÷π÷22]∶（5÷π÷32）
＝（6÷4÷π）∶（5÷9÷π）
＝∶
＝（×18π）∶（×18π）
＝27∶10
【点睛】解答此题的关键是，根据圆柱和圆锥的体积公式，找出对应量，写出圆锥与圆柱高的比，化简即可。
20．     18     216
【分析】根据长方形的周长＝（长＋宽）×2，可得长＋宽＝60÷2＝30（cm），已知长和宽的比是3∶2，长可看作3份，宽看作2份，长和宽共占（3＋2）份，可求出长占长和宽总长的，利用求一个数的几分之几是多少的计算方法，用30×求出长方形的长，继而求出长方形的宽，再利用长方形的面积公式，代入数据即可得解。
【详解】60÷2＝30（cm）
30×＝30×＝18（cm）
30－18＝12（cm）
18×12＝216（cm2）
【点睛】此题主要考查按比例分配的应用题的解答方法，利用长方形的周长和面积公式，解决实际的问题。
21．56.52
【分析】我们先设小圆的半径是r，大圆的半径是2r．然后根据圆环的面积＝大圆的面积减去小圆的面积，阴影部分的面积＝大圆半径的平方－小圆半径的平方，进一步求出环形的面积即可。
【详解】解：设小圆的半径是r，大圆的半径是2r。
圆环的面积＝3.14×[（2r）2－r2]
因为（2r）2－r2＝18
3.14×18＝56.52（cm2）
【点睛】本题运用环形的面积公式进行解答即可。
22．4
【分析】由圆柱的体积＝底面积×高，可得：圆柱的高＝圆柱的体积÷底面积；
由圆锥的体积＝×底面积×高，可得：圆锥的高＝3×圆锥的体积÷底面积，已知圆柱的体积等于圆锥的体积，圆柱的底面积等于圆锥的底面积，所以圆锥的高＝3×圆柱的高，又圆锥体的高是12厘米，所以圆柱的高就是12÷3＝4厘米。
【详解】根据分析可知一个圆柱体与和它等底的圆锥体的体积相等，圆锥体的高是12厘米，圆柱体的高是4厘米。
【点睛】本题考查圆柱的体积、底面积和高的关系，圆锥的体积、底面积和高的关系。由圆柱的体积＝底面积×高，圆锥的体积＝底面积×高，这两个公式变形可以找到等体积等底的圆柱和圆锥的高之间的关系。
23．8
【分析】把六年级学生总人数看作单位“1”，用减法计算求得书法小组人数所占的百分比，再用总人数乘以书法小组所占的百分比即可得出答案。
【详解】160×（1－30%－40%－25%）
＝160×5%
＝8（人）
答：六年级参加书法小组有8人。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用，并且能够根据统计图提供的信息解决问题。
24．     酒精     整瓶酒     240
【分析】百分数表示一个数占另一个数的百分比，52%表示酒精占整瓶酒的百分率，把整瓶酒看作单位“1”，水占整瓶酒的（1－52%），最后用乘法求出水的含量。
【详解】分析可知，52%表示酒精占整瓶酒的52%。
500×（1－52%）
＝500×0.48
＝240（mL）
所以，这瓶酒中含水240mL。
【点睛】理解百分数的意义并求出水的含量占整瓶酒的百分率是解答题目的关键。
25．30
【分析】第1个图形由（1＋1）个等腰直角三角形拼成边长为1厘米的正方形；第2个图形由（2＋1）个等腰直角三角形拼成一个直角梯形；第3个图形由（3＋1）个等腰直角三角形拼成长为[（3＋1）÷2]厘米，宽为1厘米的长方形；第4个图形由（4＋1）个等腰直角三角形拼成一个直角梯形；第5个图形由（5＋1）个等腰直角三角形拼成长为[（5＋1）÷2]厘米，宽为1厘米的长方形……从第2个图形开始，第偶数个图形拼成的为直角梯形，第奇数个图形拼成的是长方形，第27个图形拼成长为[（27＋1）÷2]厘米，宽为1厘米的长方形，最后利用“长方形的周长＝（长＋宽）×2”求出图形的周长，据此解答。
【详解】（27＋1）÷2
＝28÷2
＝14（厘米）
（14＋1）×2
＝15×2
＝30（厘米）
所以，拼成的第27个图形的周长是30厘米。
【点睛】分析图形找出拼图变化的规律是解答题目的关键。
26．     37680     25120
【分析】长方形以AB为轴旋转得到的圆柱高为30厘米，半径为20厘米，再根据圆柱的体积计算公式：V＝Sh计算出结果；把圆柱削成一个最大的圆锥，削去的体积占圆柱体积的，据此计算即可。
【详解】圆柱的体积：
20×20×3.14×30
＝400×3.14×30
＝1256×30
＝37680（立方厘米）
削去的体积：
37680×＝25120（立方厘米）
【点睛】考查了图形的旋转与圆柱的体积，本题的关键是判断出圆柱的底面半径和高以及削去体积与原来体积的关系。
27．     3∶8    
【详解】0.25∶
＝（0.25×12）∶（×12）
＝3∶8
0.25∶
＝0.25÷
＝
28．2；25；3；二
【分析】根据分数的基本性质：分数的分子分母同时乘或除以一个不为0的数，分数的大小不变；＝＝＝；再根据分数与比的关系：分子做比的前项，分母做比的后项；＝2∶10；再根据分数与除法的关系：分子做被除数，分母做除数：＝5÷25；＝，再用4－1，求出（）的值；再用1÷5，求出商，再把小数点向右移动两位，添上百分号，百分之几十就是几成，据此解答。
【详解】2∶10＝＝5÷25＝＝二折
【点睛】本题主要是考查除法、分数与比的关系；小数、分数、百分数之间的互化以及折扣问题。
29．9
【分析】将获奖总人数看作单位“1”，1－获得一等奖的对应分率－获得二等奖的对应分率－获得三等奖的对应分率＝获得优胜奖的对应分率，将分母化成大于40小于50的分数，即可确定优胜奖人数。
【详解】1－－－
＝1－－－
＝
（人）
总人数42人，获得优胜奖的有9人。
【点睛】关键是理解分数的意义，异分母分数相加减，先通分再计算。
30．7.2
【分析】根据图形放大与缩小的方法以及比例的意义可知：把这个长方形按照一定比例缩小后，对应边的比值相等；据此可列出比例6∶4.8＝9∶x，解比例即可。
【详解】6∶4.8＝9∶x
6x＝4.8×9
6x＝43.2
x＝43.2÷6
x＝7.2
【点睛】根据图形放大与缩小的方法列出比例，用解比例方法求值即可。
31．     4500     150
【分析】根据比的意义，销售总量÷总份数，求出一份数，一份数分别乘线上和线下对应份数，求出线上和线下销量；线上和线下销量的差÷线下销量＝线上销量比线下销量多百分之几。
【详解】6300÷（5＋2）
＝6300÷7
＝900（个）
900×5＝4500（个）
900×2＝1800（个）
（4500－1800）÷1800
＝2700÷1800
＝150%
【点睛】关键是理解比的意义，两数相除又叫两个数的比，差÷较小数＝多百分之几。
32．×＝
【分析】先把长方形平均分成3份，涂色部分占1份，就是，再把这1份平均分成了3份，深色部分占两份就是的，即×，由此求解。
【详解】×＝
【点睛】解决本题主要根据分数的意义以及分数乘法的意义进行解答。
33．50；八
【分析】将80%化为分数是，根据分数的基本性质，分子和分母同时乘10，则；百分之几十表示几成，所以80%表示八成。
【详解】＝80%＝八成。
【点睛】本题考查了分数和百分数的互化、分数的基本性质以及成数的意义。
34．     黄     14
【分析】盒子里红球、黄球、白球，任意摸出一个球，可能是红球，可能是黄球，可能是白球；哪种颜色的球的数量最多，摸出哪种颜色的球的可能性最大；利用抽屉原理，考虑最差情况：如果前7＋6次摸出的都是其中两个颜色的球，那么第7＋6＋1次摸到的一定是第三种颜色的球，据此解答。
【详解】7＞6＞5
7＋6＋1
＝13＋1
＝14（次）
【点睛】此题考查了利用抽屉原理解决实际问题的灵活应用，关键是从最差情况考虑。
35．     圆锥     a     底面半径     6.28b
【分析】以直角三角形的直角边所在直线为旋转轴，其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。 垂直于轴的边旋转而成的曲面叫做圆锥的底面。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。无论旋转到什么位置，不垂直于轴的边都叫做圆锥的母线。圆锥的高：圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。
【详解】下面是一个直角三角形，如果以a边为轴旋转一周，将形成一个圆锥，这个立体图形的高是a，b是它的底面半径，它的底面周长是3.14×b×2=6.28b。

【点睛】本题考查了圆锥的特征，要有一定的空间想象能力。
36．     3     3
【分析】抽屉原则二：如果把n个物体放在m个抽屉里，其中n＞m，那么必有一个抽屉至少有：
（1）当n不能被m整除时，k＝[]＋1个物体。
（2）当n能被m整除时，k＝个物体。
【详解】25÷12＝2（人）……1（人）
2＋1＝3（人）
5÷2＝2（人）……1（人）
2＋1＝3（人）
【点睛】关键是构造物体和抽屉，也就是找到代表物体和抽屉的量，然后依据抽屉原则进行计算。
37．19
【分析】根据三角形三边的关系“两边之和大于第三边，两边之差小于第三边”，选择两根8cm、一根3cm的小棒围成等腰三角形，再求出周长即可。
【详解】8＋8＋3
＝16＋3
＝19（cm）
【点睛】熟记三角形三边关系并能灵活利用是解答本题的关键。
38．
【分析】分别计算出三杯糖水中糖占糖水的几分之几，再比较三个分数的大小，即可知哪杯最甜。
【详解】第一杯：
第二杯：
第三杯：
因为＞＞，所以第三杯最甜，糖占糖水的。
【点睛】本题考查一个数是另一个数的几分之几的求法及分子是1的分数的大小比较。
39．     100     37000
【分析】1小时＝60分，1公顷＝10000平方米，据此解答。
【详解】小时＝100分
3.7公顷＝37000平方米
【点睛】本题考查了时间单位以及面积单位之间的换算，注意高级单位化低级单位要乘进率，低级单位化高级单位要除以进率。
40．128
【分析】先根据正方体的体积＝棱长×棱长×棱长，求出这个橡皮泥的体积；把这个橡皮泥做成一个等底等高的一个圆柱体和一个圆锥体，橡皮泥的体积不变，即圆柱和圆锥的体积之和等于正方体的体积；
因为圆柱和圆锥等底等高，那么圆柱的体积是圆锥的3倍，可以把圆锥的体积看作1份，则圆柱的体积是3份，总份数是（1＋3）份；用这个橡皮泥的体积除以总份数，求出一份数，即是圆锥的体积。
【详解】正方体的体积：
8×8×8
＝64×8
＝512（立方厘米）
圆锥的体积：
512÷（1＋3）
＝512÷4
＝128（立方厘米）
【点睛】本题考查正方体的体积公式、圆柱和圆锥的体积关系，明确圆柱和圆锥等底等高时，圆柱的体积是圆锥体积的3倍。
41．     24     12∶6＝2∶1
【分析】最小的质数是2，最小的合数是4，所以一个两位数，十位上是最小的质数，个位上是最小的合数，这个数是24；
根据找一个数的因数的方法，可以一对一对的找，最小的是1，最大的是它本身，然后根据比例的意义，选四个因数写出两个比值是2的比，再组成比例即可。
【详解】一个两位数，十位是最小的质数，个位是最小的合数，这个数是24，
24的因数有：1、2、3、4、6、8、12、24；
因为2∶1＝2，12∶6＝2，所以12∶6＝2∶1（答案不唯一）。
【点睛】此题主要考查求一个数的因数的方法和比例的意义，知道最小的质数是2，最小的合数是4，是解答此题的关键。
42．     12    
【分析】两个相关联的量，若比值一定，两个量成正比例关系；若乘积一定，两个量成反比例关系。
【详解】设如果A与B成正比例，则☆是x得：
10∶8＝15∶x
解：10x＝8×15
10x＝120
10x÷10＝120÷10
x＝12
设如果A与B成反比例，则☆是y，得：
15y＝10×8
解：15y＝80
15y÷15＝80÷15
y＝
【点睛】本题考查了用比例解决问题，需用等式的性质解比例。
43．     5     3
【分析】1∶400表示图上1厘米，表示实际的400厘米，将长和宽的单位化为厘米，然后分别除以400即可解答。
【详解】20米＝2000厘米
12米＝1200厘米
长：2000÷400＝5（厘米）
宽：1200÷400＝3（厘米）
【点睛】此题主要考查学生对按比例尺求取图上距离的应用。
44．0.5024
【分析】根据圆柱的体积公式：V＝πr2h，据此代入数值进行计算即可。
【详解】80cm＝0.8m
3.14×（0.8÷2）2×1
＝3.14×0.16
＝0.5024（立方米）
【点睛】本题考查圆柱的体积，熟记公式是解题的关键。
45．3
【分析】把11个苹果分给4个小朋友，即将这4个小朋友当作4个抽屉，将这11个苹果放入这四个抽屉，利用抽屉原理最差情况：要使每个人分到的苹果最少，只要使每个抽屉的元素数尽量平均分即可。
【详解】11÷4＝2（个）……3（个）
2＋1＝3（个）
所以总有一个小朋友至少分到3个苹果。
【点睛】此题考查了利用抽屉原理解决实际问题的灵活应用，关键是从最差情况考虑。
46．     10     6
【分析】先将40%化成分母为100的分数即，再约分成最简分数；
分数的基本性质：分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变；
分数与比的关系：分子相当于比的前项，分母相当于比的后项，分数线相当于比号；
分数与除法的关系：分子相当于被除数，分母相当于除数，分数线相当于除号。
【详解】40%＝＝
＝＝，＝4∶10
＝＝，＝6÷15
即4∶10＝6÷15＝40%。
【点睛】掌握分数的基本性质、分数与除法、比的关系，百分数、分数的互化是解题的关键。
47．     11.89万     27亿
【分析】改写成用“万”作单位的数，就是在万位的右下角点上小数点，然后把小数末尾的0去掉，再在数的后面写上“万”字；省略亿位后面的尾数，就是四舍五入到亿位，再在数的后面写上“亿”字，据此解答。
【详解】118900记作11.89万；
2688000000≈27亿
【点睛】本题考查整数的改写和求近似数，注意结果要带计数单位。
48．18
【分析】根据正方体表面积＝棱长×棱长×6，求出一个小正方体表面积，再乘7，是原来7个小正方体表面积和；拼成的几何体，看上去表面积比大正方体少了3个小正方形，里面有出现了同样的3个小正方形，所以拼成的几何体的表面积＝8个小正方体拼成的大正方体的表面积，求出大正方体表面积，与原来7个小正方体表面积和求差即可。
【详解】1×1×6×7＝42（cm2）
1＋1＝2（cm）
2×2×6＝24（cm2）
42－24＝18（cm2）
【点睛】关键是掌握并灵活运用正方体表面积公式。
49．     12.56     125.6
【分析】（1）这个长方体的底面积其实就是圆柱体的底面积，因此求出圆柱体的底面积即可。
（2）长方体的体积与圆柱体的体积相等，只是形状发生了变化，但体积是相等的。
【详解】（1）3.14×22＝12.56（平方厘米）
（2）3.14×22×10
＝12.56×10
＝125.6（立方厘米）
答：这个长方体的底面积是12.56平方厘米，体积是1256立方厘米。
故答案为：12.56，125.6
【点睛】本题考查了学生的转化思想，转化后的图形与原图形密不可分，同时考查了圆柱体的体积公式及表面积公式的运用情况。
50．     96     30     500
【分析】根据1时＝60分，1吨＝1000千克，进行换算即可。
【详解】1.6×60＝96（分）；0.5×1000＝500（千克），30.5吨＝30吨500千克
【点睛】关键是熟记单位间的进率，单位大变小乘进率。
51．     204     200
【详解】240×85%＝204（元）
170÷85%＝200（元）
52．     8     24
【分析】根据正方体的体积公式：V＝a3，求出水的体积，然后根据圆柱的体积公式：V＝Sh，据此可求出圆柱形容器的高；再根据圆锥的体积公式：V＝Sh，据此求出圆锥形容器的高。
【详解】4×4×4÷8
＝16×4÷8
＝64÷8
＝8（dm）
4×4×4×3÷8
＝64×3÷8
＝192÷8
＝24（dm）
【点睛】本题考查圆柱和圆锥的体积，熟记公式是解题的关键。
53．     百分之三十五          7265
【分析】百分数的读法：先读百分之几，再读百分号前面的数，由此填空；百分之几就是分母是100，分子是百分号前面的数，再根据分数的基本性质约分即可；四舍五入到亿位，即看千万位上的数，如果千万位上的数大于等于5，即进一，小于5即舍去。
【详解】由分析可知：35%读作：百分之三十五
改成最简分数：35%＝＝
726541000000四舍五入到亿位是7265亿。
【点睛】本题主要考查百分数的读法、约分的方法以及整数的近似数，应熟练掌握它们的知识并灵活运用。
54．480
【分析】要求AB两城市间的实际距离是多少千米，根据“图上距离÷比例尺＝实际距离”，代入数值，计算即可。
【详解】8÷＝48000000（cm）
48000000cm＝480km
【点睛】此题有计算公式可用，根据图上距离、比例尺和实际距离三者的关系，进行分析解答即可得出结论。
55．     1.01、﹢4.9、﹢     ﹣8、﹣、﹣80%
【分析】正数前面可以加“﹢”号，也可不加，负数都带“﹣”号，0既不是正数也不是负数，据此解答即可。
【详解】在1.01、0、﹣8、﹢4.9、﹣、﹢、﹣80%这些数中，正数有1.01、﹢4.9、﹢，负数有﹣8、﹣、﹣80%。
【点睛】本题是考查正、负数的意义。在数轴上，位于0左边的数都是负数，位于0右边的数都是正数。
56．6∶1
【分析】根据图上距离∶实际距离＝比例尺，写出比化简即可。
【详解】3cm∶5mm＝30mm∶5mm＝6∶1
【点睛】比例尺没有单位名称。为了方便，通常把比例尺的前项化作1（图上距离大于实际距离的，常把后项化为1）。
57．     1∶200     30
【分析】根据比例尺＝图上距离∶实际距离，实际距离＝图上距离÷比例尺，代入数据解答即可。
【详解】6厘米∶12米
＝6厘米∶1200厘米
＝1∶200
15÷＝3000（厘米）
3000厘米＝30米
【点睛】解答此题的关键是掌握比例尺的相关公式。
58．1∶2∶3
【分析】根据比的基本性质，若a∶b＝1∶2，a∶c＝1∶3，假设a＝1，则b＝2，c＝3，由此可以得出a∶b∶c＝1∶2∶3，由此解答即可。
【详解】由分析可知；若a∶b＝1∶2，a∶c＝1∶3则a∶b∶c＝1∶2∶3。
【点睛】此题关键是利用比的性质，把数字比的前项和后项分别扩大一定的倍数，让b在两个比例中所占的份数相同，然后合并。
59．(1)     32     22
(2)     30     20

【分析】（1）将选择剪纸的男、女生人数加起来求出选择剪纸的人数；将选择武术的男、女生人数加起来求出选择武术的人数，将选择舞蹈的男、女生人数加起来求出选择舞蹈的人数，再用选择武术的人数减去选择舞蹈的人数即可；
（2）将选择剪纸、武术、舞蹈的人数总和求出来，再除以3求出平均选择每个活动课程的有多少人；先计算出选择剪纸的人数比选择武术的少的人数，再除以选择武术的人数最后乘100%即可。
（1）
选择剪纸的有：14＋18＝32（人）
选择武术的有：30＋10＝40（人）
选择舞蹈的有：6＋12＝18（人）
选择武术的学生比选择舞蹈的多：40－18＝22（人）
（2）
（32＋40＋18）÷3
＝90÷3
＝30（人）
（40－32）÷40
＝8÷40
＝0.2
＝20%
【点睛】本题考查复式条形统计图的应用，读懂统计图并从中得到必要的信息是解决问题的关键。
60．     200.96     50.24
【分析】首先要明确分针1小时（60分钟）转1周，转1周针尖端走的路程是一个圆的周长，根据圆的周长公式C＝2πr即可求解；分针走一个小时转1周，扫过的面积即半径是8cm圆的面积，根据圆的面积公式：S＝πr2，把数据代入公式进行解答。
【详解】3.14×82＝200.96（cm2）
3.14×（8×2）
＝3.14×16
＝50.24（cm）
【点睛】此题解答关键是明确分针的尖端1小时行走了钟表的一圈，然后根据圆的周长和面积公式解决问题。
61．2.4
【分析】从甲筐倒出20%给乙筐，则两筐一样重，可知乙筐的草莓质量比甲筐少2个20%，据此解答。
【详解】1.44÷（1－20%－20%）
＝1.44÷0.6
＝2.4（千克）
【点睛】本题考查了利用百分数除法解决问题，解决本题的关键是分析出乙筐草莓占甲筐的几分之几。
62．         
【分析】求每段的长度，是把6米长的铁丝平均分成7段，用这根铁丝的长度除以7；
把这根铁丝的全长看作单位“1”，平均分成7段，求每段是这根铁丝的几分之几，用1除以7。
【详解】6÷7＝（米）
1÷7＝
【点睛】解决此题关键是弄清求的是“分率”还是“具体的数量”，求分率：平均分的是单位“1”；求具体的数量：平均分的是具体的数量。注意：分率不带单位名称，而具体的数量要带单位名称。
63．157
【分析】通过圆锥的底面周长，计算出圆锥的底面半径，再利用圆锥的体积公式算出结果。
【详解】




【点睛】此题的解题关键是利用圆锥的体积公式求解。
64．3
【分析】由题意可知，根据求一个数的几分之几是多少，用乘法先求出第一次剪去的部分的长度，然后用绳子的长度分别减去第一次和第二次剪去的长度即可求出剩下的长度。
【详解】5－5×－
＝5－－
＝5－2
＝3（m）
【点睛】本题考查分数带单位和不带单位的区别，明确分数带单位表示具体的量，不带单位表示分率是解题的关键。
65．     150     15
【分析】由于选择B的有66名学生，选择B的人数占总人数的44%，单位“1”是总人数，单位“1”未知，用除法，即66÷44%＝150（人），由于总人数是单位“1”，用1减选择A、B、D占总人数的百分比即可求出选择C的人数占了总人数的百分之多少，再用总人数分别乘选择C和选择D所占的百分比，由此即可求出选择C和D的人数，之后用选择D的人数减选择C的人数即可。
【详解】66÷44%＝150（人）
1－30%－18%－44%＝8%
150×18%－150×8%
＝27－12
＝15（人）
【点睛】本题主要考查扇形统计图的应用，同时找准单位“1”，单位“1”已知，用乘法，单位“1”未知，用除法。
66．     120     20
【详解】略
67．     反     10
【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定，如果是比值一定，就成正比例，如果是乘积一定，则成反比例；把ab的值代入ab－25，计算即可解答。
【详解】因为＝（a和b都是不为0的自然数），所以ab＝35（一定）；乘积一定，a和b成反比例。
ab－35
35－25＝10
【点睛】根据正比例意义以及辨识，反比例意义以及辨识进行解答。
68．500
【分析】将原价看作单位“1”，打七五折销售，现价是原价的75%，比原来便宜了1－75%，原价×便宜的对应百分率＝便宜的钱数，据此分析。
【详解】2000×（1－75%）
＝2000×0.25
＝500（元）
【点睛】关键是理解折扣的意义，几折就是百分之几十。
69．     60     59
【分析】观察图形：第1个图案中有4×2＝8个小正方形，第2个图案中有4×3＝12个小正方形，第3个图案中有4×4＝16个小正方形，……所以第n个图案中有4（n＋1）个小正方形。
【详解】根据分析得到的规律可知第14个图中有小正方形：
4×（14＋1）
＝4×15
＝60（个）
第n个图案中有240个小正方形，可得：
4（n＋1）＝240
4n＋4＝240
4n＝236
n＝59
【点睛】此题考查图形的变化规律，解决本题的关键是找出图形之间的运算规律，利用规律解决问题。
70．5∶7
【分析】因为红花种植面积占圆形花池面积的，占长方形花池面积的，假设红花种植面积有2份，则圆形花池面积是7份，则长方形花池面积是9份，则种植的黄花面积有：（7－2）份，种植粉花的面积有（9－2）份，据此解答。
【详解】假设红花种植面积有2份，则圆形花池面积是7份，则长方形花池面积是9份，则种植的黄花面积有：（7－2）份，种植粉花的面积有（9－2）份，
则种植的黄花与粉花的面积比是：（7－2）∶（9－2）＝5∶7。
【点睛】此题应结合题意，运用假设法，设出红花种植面积的份数，进而求出种植的黄花面积和粉花面积的份数，是解答此题的关键。
71．     18     6
【详解】圆锥的体积为：12÷2＝6（立方分米）
圆柱体的体积：12＋6＝18（立方分米）
答：这个圆柱的体积是18立方分米，圆锥的体积是6立方分米。
72．     176     192     8
【分析】求需要玻璃的多少，即求长方体五个面的面积，根据长方体五个面的面积公式：S＝（ah＋bh）×2＋ab，据此求出需要玻璃的面积；根据长方体的容积公式：V＝abh，据此求出长方体中水的体积；用水的体积除以圆柱形容器的底面积即可求出水的高度，再根据求一个数的百分之几是多少，用乘法取出水面的高度是多少。
【详解】（8×6＋4×6）×2＋8×4
＝（48＋24）×2＋32
＝72×2＋32
＝144＋32
＝176（平方分米）
8×4×6
＝32×6
＝192（立方分米）
192÷24＝8（分米）
【点睛】本题考查长方体的表面积和体积，熟记公式是解题的关键。
73．     6     16     75     0.75
【分析】先用分数的分子除以分母把分数化为小数，再把小数的小数点向右移动两位，添上百分号“%”把小数化为百分数，最后根据“”利用商不变的规律和比的基本性质求出被除数和比的后项，据此解答。
【详解】＝3÷4＝0.75＝75%
＝3÷4＝3∶4
3÷4＝（3×2）÷（4×2）＝6÷8
3∶4＝（3×4）∶（4×4）＝12∶16
【点睛】掌握比、分数、除法之间的关系是解答题目的关键。
74．射（√）
【分析】根据正方体展开图的特征可知，与“14”相对的面是“功”，与“成”相对的面是“发”，与“神”相对的面是“射”，据此解答即可。
【详解】由分析可知：
与“神”字相对面上的字是“射”字。
【点睛】本题考查正方体的展开图，明确正方体中各个相对的面是解题的关键。
75．     3385850000     34
【分析】根据整数的写法，从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0，即可写出此数；
省略“亿”位后面的尾数，把亿位后的千万位上的数进行四舍五入，再在数的后面写上“亿”字，据此解答。
【详解】截至2022年6月7日，我国累计报告接种疫苗为三十三亿八千五百八十五万次，横线上的数写作3385850000，省略亿位后面的尾数约是34亿。
【点睛】本题考查了整数的写法和求近似数，注意求近似数时要带计数单位。
76．1350
【分析】根据实际距离＝图上距离÷比例尺，进行换算即可。
【详解】2.7÷＝135000000（厘米）＝1350（千米）
太原到上海的实际距离约为1350千米。
【点睛】关键是掌握图上距离与实际距离的换算方法。
77．     192     144
【分析】把国旗的长或宽设为未知数，根据国旗长和宽的比是3∶2用比例的知识解答，并利用比例的基本性质求出未知数，据此解答。
【详解】解：设1号国旗的宽为xcm。
288∶x＝3∶2
3x＝288×2
3x＝576
x＝576÷3
x＝192
所以，1号国旗长288cm，宽192cm。
解：设4号国旗长ycm。
y∶96＝3∶2
2y＝96×3
2y＝288
y＝288÷2
y＝144
所以，4号国旗长144cm，宽96cm。
【点睛】解题时也可以根据按比例分配的解题方法求出长或宽的长度。
78．     3     60     30     六
【分析】把化简为，根据分数与比的关系，＝3∶5；根据分数与除法的关系，＝3÷5，根据商不变的规律，3÷5＝18÷30；把化成小数为0.6，把0.6的小数点向右移动两位，再加上百分号就是60%；根据折扣的意义，60%就是六折；据此解答即可。
【详解】3∶5＝60%＝＝18÷30＝六折
【点睛】本题考查比、百分数、小数、分数的互化，分数与除法的关系，商不变的规律，折扣的意义。
79．
【分析】在比例中，两个内项的乘积等于两个外项的乘积，另一个外项＝两个内项的乘积÷其中一个外项，再根据最小的质数为2，即可求得。
【详解】分析可知，最小的质数是2。
2÷＝
【点睛】掌握比例的基本性质是解答题目的关键。
80．     2400     2412
【分析】药粉和水的比是1∶200，即水的质量是药粉的200倍，所以用药粉乘200求出需要加的水，再用水加药粉就等于药水。
【详解】12×200＝2400（千克）
2400＋12＝2412（千克）
【点睛】本题考查了比的问题，关键是根据比的意义先求出水的质量。
81．     0.45     9     6.03     4.5
【分析】根据1平方千米＝100公顷，1时＝60分，1千克＝1000克，1升＝1000立方厘米，进行换算即可。
【详解】45÷100＝0.45（平方千米）；0.15×60＝9（分）
30÷1000＝0.03（千克），6千克30克＝6.03千克；4500÷1000＝4.5（升）
【点睛】单位大变小乘进率，单位小变大除以进率。
82．(1)正
(2)反

【分析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定，如果是比值一定，就成正比例，如果是乘积一定，则成反比例。
【详解】（1）图上距离÷实际距离＝比例尺（一定），图上距离与实际距离成正比例关系；
（2）单价×数量＝总价，购买物品的总价一定，购买的数量和单价成反比例关系。
【点睛】此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再作判断。
83．     11.304     43.2
【分析】根据圆锥体积＝底面积×高÷3，求出陀螺体积；长方体盒子的长和宽至少等于陀螺底面直径，长方体的高至少等于陀螺的高，根据长方体体积＝长×宽×高，求出盒子容积即可。
【详解】3.14×（4÷2）2×2.7÷3
＝3.14×4×0.9
＝11.304（cm3）
4×4×2.7＝43.2（cm3）
这个陀螺的体积是11.304cm3；这个盒子的容积至少是43.2cm3。
【点睛】关键是掌握并灵活运用圆锥和长方体的体积公式。
84．6；35；20；40；四
【分析】根据已知的小数0.4，可以把小数化成分数为，根据分数的基本性质，把的分子和分母同时乘4就是；根据分数与除法的关系，＝2÷5，根据商不变的规律，2÷5＝6÷15；根据分数与比的关系，＝2∶5，根据比的基本性质，2∶5＝14∶35；把0.4的小数点向右移动两位，再加上百分号就是40%；根据折扣的意义，40%＝四折，据此解答即可。
【详解】6÷15＝0.4＝14∶35＝＝40%＝四折。
【点睛】本题考查了百分数、分数、比、小数的互化，并利用商不变的规律、比的基本性质等知识。
85．     5n＋1     11
【分析】观察可知，小棒根数＝六边形数量×5＋1，六边形个数＝（小棒根数－1）÷5，据此分析。
【详解】n×5＋1＝（5n＋1）根
（56－1）÷5
＝55÷5
＝11（个）
摆n个六边形需要（5n＋1）根小棒；如果有56根小棒，可以摆11个六边形。
【点睛】字母可以表示任意的数，也可以表示特定含义的公式，用字母将数量关系表示出来。
86．     ﹣94     少
【分析】用正负数表示意义相反的两种量：上车人数记作正，则下车人数就记作负。由此得解。
【详解】一列高铁在济南西站上车的乘客是62名，记作﹢62名，下车的乘客是94名，记作﹣94名；
62＜94
此时高铁上的人数比原来少。
【点睛】此题主要考查正负数的意义，正数与负数表示意义相反的两种量，看清规定哪一个为正，则和它意义相反的就为负。
87．80
【分析】阴影部分可以拼成一个圆，如图，将正方形平均分成4个小正方形，小正方形的边长＝圆的半径，根据圆的面积＝πr2，求出r2，即每个小正方形的面积，乘4即可。
【详解】62.8÷3.14＝20
20×4＝80（平方厘米）
正方形的面积是80平方厘米。
【点睛】关键是掌握并灵活运用正方形和圆的面积公式。
88．     49     n2
【分析】由题可知，1×1＝1，2×2＝4，3×3＝9，4×4＝16……规律：第几幅图点子数就是几的平方；据此解答即可。
【详解】7×7＝49（个）
第n幅图的点子总数是n2个。
【点睛】解答本题关键是找到变化规律。
89．(1)     6.2     ﹣8.5
(2)350
(3)90
(4)50%

【分析】根据题中的数据特点，先确定温度可能为负数，则冰面温度为﹣8.5℃；再根据生活实际确定高铁时速为350千米/时；1小时＝3600秒，25×3600÷1000＝90千米/时，则“猎豹”高速摄像系统技术标准能达到25米/秒，约等于时速90千米/时；综合节能达到50%；最后确定国家游泳中心占地面积为6.2公顷，据此解答。
（1）
“双奥场馆”国家游泳中心占地面积6.2公顷，通过“水冰转换”成为冬奥会历史上最大体量的冰壶场馆，冰壶赛道冰面温度仅有﹣8.5℃，冰面以上1.5米处温度保持在10℃，看台温度16℃至18℃，既满足了冰壶比赛环境的需要，又为观众营造了舒适的观赛环境。
（2）
京张高铁是北京冬奥会专用通道，也是我国首条建成投用的5G智能高铁，实现了时速350千米自动驾驶功能，具备车站自动发车、区间自动运行、到站自动停车、自动门控等先进功能。
（3）
在冬奥会速滑比赛中，运动员速度可达到15—18米/秒，而我国研发的“猎豹”高速摄像系统技术标准能达到25米/秒，约等于时速90千米，能灵活地捕捉速滑中的各种场面，让比赛更加公平公正。
（4）
首都体育馆同时承办花样滑冰和短道速滑两个项目，项目组二氧化碳快速“造冰”技术打造“最快冰面”，综合节能达到50%以上，达到国际先进水平。
【点睛】本题主要考查了数在生活中的应用，联系生活实际根据数的特点先找出比较好确定的数据是解答题目的关键。
90．
【分析】把这批零件的总数看作单位“1”，根据工作效率＝工作总量÷工作时间，计算师徒二人的工作效率，再用工作总量除以二人工作效率的和，求工作时间。
【详解】1÷（1÷8＋1÷12）
＝1÷（＋）
＝1÷
＝（小时）
【点睛】本题主要考查简单的工程问题，关键是利用工作总量、工作时间和工作效率的关系做题。
91．5亿；8524.1016万；二十二万三千四百八十八；
【分析】省略“亿”位后面的尾数求近似数，根据千万位上数字的大小来确定用“四舍”法、还是用“五入”法；
改写成用“万”作单位的数，就是在万位数的右下角点上小数点，然后把小数末尾的0去掉，再在数的后面写上“万”字；
根据整数的读法，从高位到低位，一级一级地读，每一级末尾的0都不读出来，其余数位连续几个0都只读一个零，即可读出此数；
现将中美两国确诊人数估算为与之相近的整数，用中国大陆的确诊患者人数除以美国确诊的病例，就是中国大陆的确诊患者人数约为美国的几分之几。
【详解】528779944≈5亿
85241016＝8524.1016万
223488读作：二十二万三千四百八十八
8524.1016万≈8524万，223488≈22万
经过估算，中国大陆的确诊患者人数约为美国的22÷8524＝
【点睛】本题主要考查整数的读法、改写、求近似数及求一个数是另一个数的几分之几，注意改写和求近似数时要带计数单位。
92．21
【分析】三角形的面积是与其等底等高的平行四边形面积的一半，用42除以2，即可求出三角形的面积，据此解答。
【详解】42÷2＝21（dm2）
【点睛】此题考查的目的是理解掌握等底等高的三角形和平行四边形面积之间的关系及应用。
93．     ﹣550     潜艇
【分析】用正负数表示意义相反的两种量：海平面以上记作正，则海平面以下就记作负。由此得解。
【详解】﹣（150＋400）＝﹣550（米）
﹣150米＞﹣550米
所以，潜艇的位置比较低。
【点睛】此题主要考查正负数的意义，正数与负数表示意义相反的两种量，看清规定哪一个为正，则和它意义相反的就为负。
94．251.2
【分析】根据条件“一个圆柱的底面半径是4cm，高是10cm”，分别利用公式解答，圆柱的侧面积＝底面周长×高，据此解答。
【详解】3.14×4×2×10
＝3.14×8×10
＝25.12×10
＝251.2（cm2）
【点睛】本题考查了圆柱的侧面积公式的应用。
95．     1、2、3、4、6、9、12、18、36     1∶12＝3∶36
【分析】36的因数有：1、2、3、4、6、9、12、18、36，从这几个数中，选出四个，每两个组成比，根据比例的意义，如果这两个比的比值相同，这四个数就组成一个比例，要注意比值最小这个条件。
【详解】36的因数有：1、2、3、4、6、9、12、18、36。
根据比例的意义可得：1∶12＝3∶36。
【点睛】此题主要考查求一个数的因数的方法和比例的意义。
96．510
【分析】图上距离和比例尺已知，依据“实际距离＝图上距离÷比例尺”，代入数据即可求出两地间的实际距离，由此解答即可。
【详解】3÷＝51000000（cm）
51000000cm＝510km
【点睛】此题主要考查图上距离、实际距离和比例尺的关系，解答时要注意单位的换算。
97．     41.4     78.5
【分析】由“半径为5厘米的圆沿半径分成若干等份，再拼成一个近似的长方形”，得出长方形的周长是圆的周长再加上圆的直径。根据题意得出圆的面积就是长方形的面积，由此根据圆的面积公式S＝πr2，列式解答即可。
【详解】3.14×5×2＋5×2
＝31.4＋10
＝41.4（厘米）
3.14×52＝78.5（平方厘米）
【点睛】解答本题的关键是知道拼成的近似长方形与圆之间的关系，进而解决问题。
98．5
【分析】一年有12个月，那么把这12个月看做12个抽屉，要求至少有多少名同学在同一个月过生日，可以考虑最差情况：54个人尽量平均分配在12个抽屉中，利用抽屉原理即可解答。
【详解】54÷12＝4⋯⋯6
4＋1＝5（人）
【点睛】此题考查了抽屉原理解决实际问题的灵活应用。
99．     14     3n－1
【分析】第1个图案有2个正方形；第2个图案比第1个图案增加了2个小正方形和1个由4个小正形组成的正方形，有5个正方形；第3个图案比第2个图案增加了2个小正方形和1个由4个小正形组成的正方形，有8个正方形……后一个图案比前一个图案多3个正方形，图案序数与正方形个数的关系是：正方形个数＝图案序数×3－1。
【详解】5×3－1
＝15－1
＝14（个）
第5个图案中有14个正方形；
第n个图案中有（3n－1）个正方形。
【点睛】本题主要考查数与形结合的规律，发现后一个图案比前一个图案增加2个小正方形和1个由4个小正方形组成的正方形是解本题的关键。