湖南省常德市安乡县2022-2023学年八年级下学期期中质量检测数学试卷

安乡县2023年上学期期中质量监测问卷

八年级数学

时量：120分钟  满分：120分

命题：李泽春   校稿：李泽春

一、选择题（本大题共有8小题，每小题3分，共24分。在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置）

1．下列各组数据为边长作三角形，其中不能组成直角三角形的是（    ）

A．4，6，8     B．5，12，13     C．6，8，10    D．7，24，25

2．如下图，某研究性学习小组为测量学校A与河对岸工厂B之间的距离，在学校附近选一点C，利用测量仪器测得．据此，可求得学校与工厂之间的距离AB等于（    ）

A．        B．       C．        D．

3．下列图形中，是中心对称图形的是（    ）

A．   B．   C．   D．

4．一个多边形的内角和为，则这个多边形是（）

A．三角形      B．四边形      C．五边形      D．六边形

5．矩形具有而平行四边形不一定具有的性质是（    ）

A．对边相等     B．对角相等      C．对角线相等    D．对角线互相平分

6．如图，在矩形ABCD中，DE平分交BC于点E，连接AE，若，则AD的长为（    ）

A．12        B．14       C．16         D．20

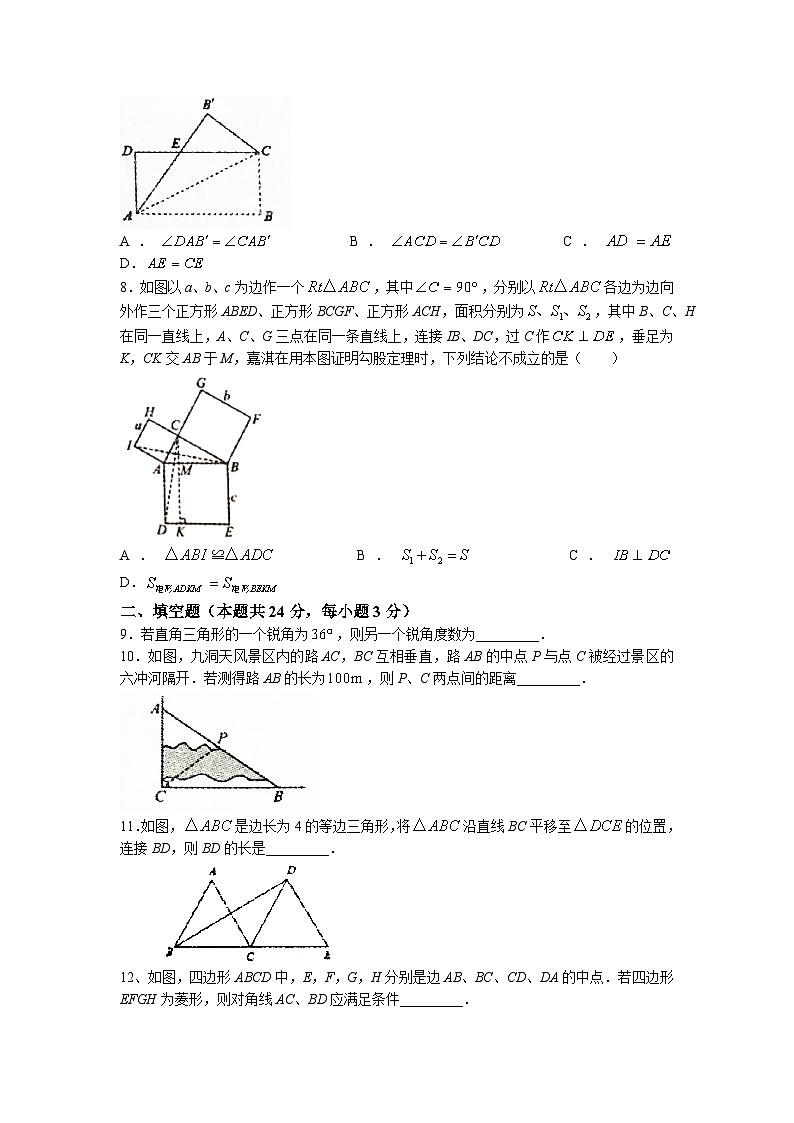
7．如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为，与DC相交于点E，则下列结论一定正确的是（    ）

A．     B．    C．      D．

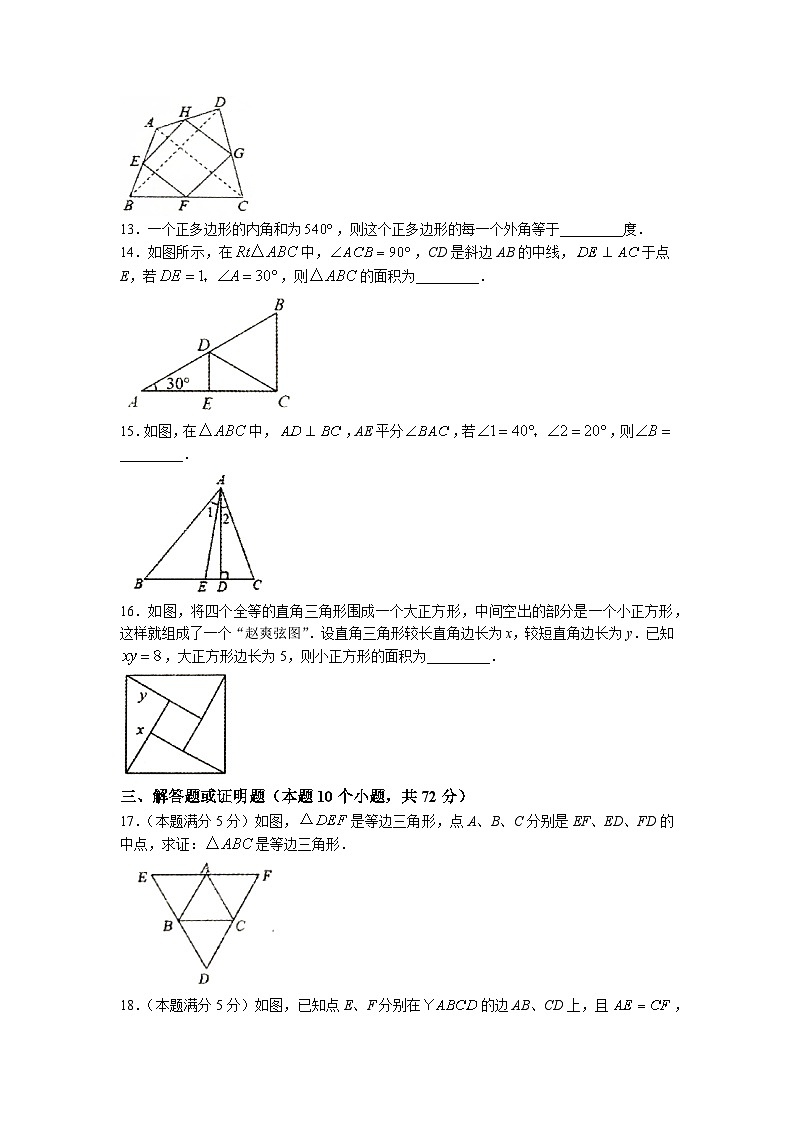
8．如图以a、b、c为边作一个，其中，分别以各边为边向外作三个正方形ABED、正方形BCGF、正方形ACH，面积分别为，其中B、C、H在同一直线上，A、C、G三点在同一条直线上，连接IB、DC，过C作，垂足为K，CK交AB于M，嘉淇在用本图证明勾股定理时，下列结论不成立的是（    ）

A．     B．      C．      D．

二、填空题（本题共24分，每小题3分）

9．若直角三角形的一个锐角为，则另一个锐角度数为_________．

10．如图，九洞天风景区内的路AC，BC互相垂直，路AB的中点P与点C被经过景区的六冲河隔开．若测得路AB的长为，则P、C两点间的距离_________．

11．如图，是边长为4的等边三角形，将沿直线BC平移至的位置，连接BD，则BD的长是_________．

12、如图，四边形ABCD中，E，F，G，H分别是边AB、BC、CD、DA的中点．若四边形EFGH为菱形，则对角线AC、BD应满足条件_________．

13．一个正多边形的内角和为，则这个正多边形的每一个外角等于_________度．

14．如图所示，在中，，CD是斜边AB的中线，于点E，若，则的面积为_________．

15．如图，在中，，AE平分，若，则_________．

16．如图，将四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”．设直角三角形较长直角边长为x，较短直角边长为y．已知，大正方形边长为5，则小正方形的面积为_________．

三、解答题或证明题（本题10个小题，共72分）

17．（本题满分5分）如图，是等边三角形，点A、B、C分别是EF、ED、FD的中点，求证：是等边三角形．

18．（本题满分5分）如图，已知点E、F分别在的边AB、CD上，且，求证：．

19．（本题满分6分）如图，在中，，高BE、CF交于点O，求的度数．

20．（本题满分6分）如图，一架梯子AB长13米，斜靠在一面墙上，梯子底端离墙5米．

（1）这个梯子的顶端距地面有多高？

（2）如果梯子的顶端下滑了5米，那么梯子的底端在水平方向滑动了多少米？

21．（本题满分7分）如图，在涪江笔直的河流一侧有一旅游地C，河边有两个景点A、B．其中，因C到A的路不通，为方便游客决定在河边新建一个景点H（A、H、B三点在同一直线上），并新修一条路CH，测得千米，千米，千米．

（1）判断的形状，并说明理由；

（2）求原路线AC的长．

22．（本题满分7分）如图，在中，D、E分别为AB、AC的中点，过点C作交DE的延长线于点F．

（1）求证：四边形BCFD为平行四边形；

（2）若，求EF的长．

23．（本题满分8分）如图，四边形ABCD中，，点E为CD的中点，射线BE交AD的延长线于点F，连接CF．

（1）求证：四边形BCFD是菱形；

（2）若，求BF的长．

24．（本题满分8分）如图，四边形ABCD中，，E、F分别是BD、AC的中点．

（1）请你猜测EF与AC的位置关系，并给予证明；

（2）当时，求EF的长．

25．（本题满分10分）【阅读】定义：如果一个三角形有两个内角的差为，那么这样的三角形叫做“准直角三角形”

【理解】（1）①若，则_________“准直角三角形”；（填“是”或“不是”）

②已知是“准直角三角形”，且，求的度数．

【应用】（2）如图，在中，点D在AC上，连接BD．若，，，，试说明是“准直角三角形”．

26．（本题满分10分）如图1，O是平行四边形ABCD对角线的交点，过点O作，垂足分别为H，M，若，我们称是平行四边形ABCD的心距比．

（1）如图2，四边形ABCD是矩形，，则_________．

（2）如图3，四边形ABCD是平行四边形，，求证：四边形ABCD是菱形．

（3）已知如图，在中，，点E、F、G分别在AB、AC、BC边上，若存在一个四边形BEFG是平行四边形，且，请通过尺规作图作出一个点F（不写作法，但保留作图痕迹；如若有必要，可简述作图思路）

安乡县2023年上学期期中质量监测

八年级数学参考答案

一、选择题（本大题共有8小题，每小题3分，共24分）

A D A B   C B D D

二、填空题（本题共24分，每小题3分）

9．     10．    11．     12．      13．

14．    15．       16．9

三、解答题或证明题（10小题，共72分）

17（本题满分5分）

证明：是等边三角形，

，                          1分，

点A、B、C分别是EF、ED、FD的中点，

                     3分

，                          4分

是等边三角形．                          5分

18题（本题满分5分）

证明：四边形ABCD是平行四边形，

．                          2分

．

，                          3分

四边形EBFD是平行四边形，                          4分

．                          5分

19（本题满分6分）

解： BE、CF是的高，

，                          2分

．                          6分

20（本题满分6分）

解：根据勾股定理：所以梯子距离地面的高度为：（米）；

答：这个梯子的顶端距地面有12米高；                          3分

（2）解：梯子下滑了5米即梯子距离地面的高度为（米），

根据勾股定理：（米），

米

答：当梯子的项端下滑5米时，梯子的底端在水平方向后移了米．                6分

21（本题满分7分）．

（1）解：是直角三角形，

理由是：在中，

，，

，

是直角三角形且；                          3分

（2）设千米，则千米，

在中，由已知得，

由勾股定理得：

，

，

解得，

答：原来的路线AC的长为千米．                          7分

22（本题满分7分）

（1）证明：

D、E分别为AB、AC的中点，

为的中位线，

∴DEBC，即DFBC，

又CFBD，

四边形BCFD为平行四边形．                          3分

（2）为的中位线，

，

四边形BCFD为平行四边形，

，

．                          7分

23（本题满分8分）

解：（1），

，

点E为CD的中点，

∴，

在与中，

，

，

，                             3分

又，

∴四边形BCFD为平行四边形，                          4分

，

四边形BCFD是菱形；                          5分

（2）四边形BCFD是菱形，

，

在中，，

，在中，．                8分

24（本题满分8分）

（1）．                          1分

理由如下：

连接AE、CE，

，E为BD中点，

，

，

，

，                         3分

F是AC中点，

；                          5分

（2），E、F分别是边AC、BD的中点，

，                          7分

25（本题满分10分）

解：（1）①在中，，

，

，

∴是“准直角三角形”，

故答案为：是；                                 2分

②是“准直角三角形”，且，

，

又，

，

，

，

若，则，

故答案为：或；                          5分（只求出一种情况的得4分）

（2），

，                6分

，

，                          7分

又，

，

是直角三角形，即，                               8分

，

，

是“准直角三角形”．                          10分

26．（1）解：四边形ABCD是矩形，

，

，

，

，

．                                      2分

（2），

，

，

又，

，

四边形ABCD是平行四边形，

，

，

，

四边形ABCD是菱形；                                    6分

（3）如图，以点C为圆心，CB为半径作弧，交AB于点D，作BC的垂直平分线交CD于Q，连接BQ，并延长交AC于点F，则点F为所求点，

理由如下：过F作交BA于E，过F作交BC于G，连接EG，交BF于O，过O作于H，过O作于M，

由作图可得：，而，

，

由作图可得：作BC的垂直平分线交CD于Q，

，

，

，

在中，，

在中，，

，即．                       10分

（只要作出BF，使就可以给满分）