

海南省2022届高三高考全真模拟卷(四)数学试题-(含答案)
展开海南省2022届高三高考全真模拟卷(四)数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知集合,则( )
A. B. C. D.
2.已知复数z满足,,则z为实数的一个充分条件是( )
A. B. C. D.
3.设随机变量,若,则a的值为( )
A.1 B.2 C.3 D.4
4.有一组样本数据如下:
56,62,63,63,65,66,68,69,71,74,76,76,77,78,79,79,82,85,87,88,95,98
则其25%分位数、中位数与75%分位数分别为( )
A.65,76,82 B.66,74,82 C.66,76,79 D.66,76,82
5.若抛物线上的点到焦点的距离是点到轴距离的3倍,则等于( )
A. B. C. D.
6.某三棱柱的平面展开图如图,网格中的小正方形的边长均为1,是线段上的点,则在原三棱柱中,的最小值为
A. B. C. D.
7.将函数的图象向右平移1个单位长度后,所得函数的图象大致为( )
A. B. C. D.
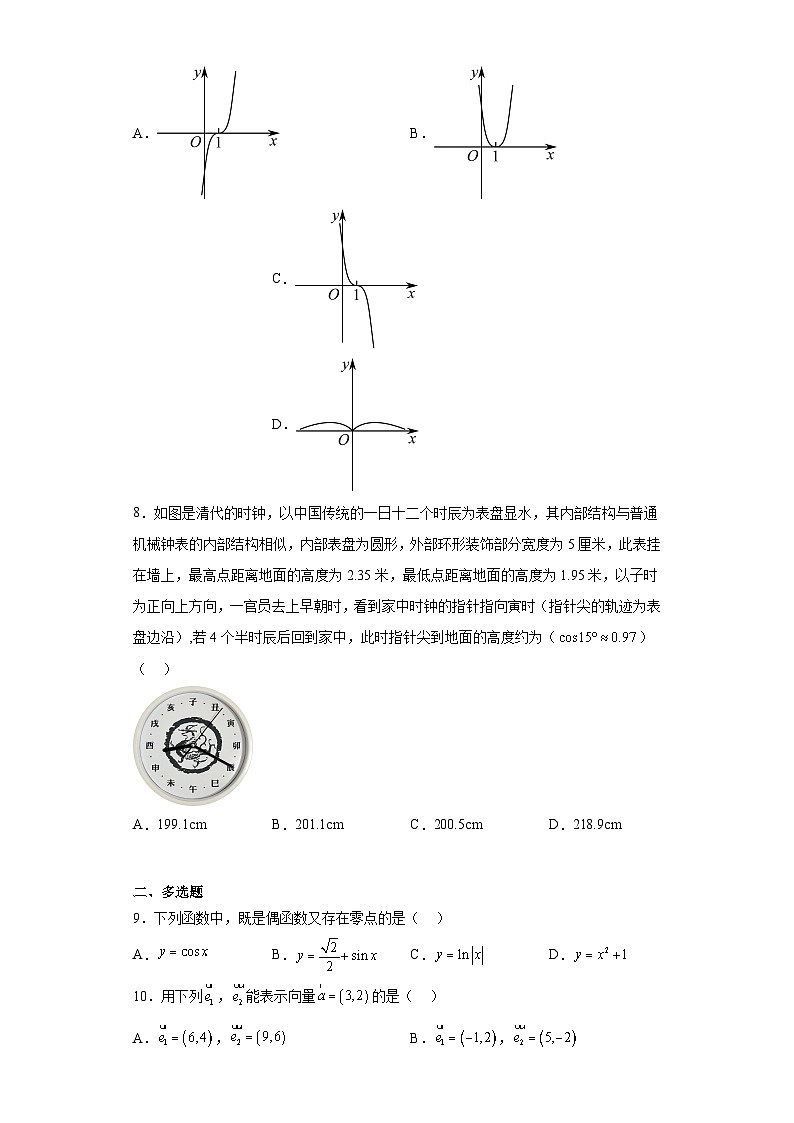
8.如图是清代的时钟,以中国传统的一日十二个时辰为表盘显水,其内部结构与普通机械钟表的内部结构相似,内部表盘为圆形,外部环形装饰部分宽度为5厘米,此表挂在墙上,最高点距离地面的高度为2.35米,最低点距离地面的高度为1.95米,以子时为正向上方向,一官员去上早朝时,看到家中时钟的指针指向寅时(指针尖的轨迹为表盘边沿),若4个半时辰后回到家中,此时指针尖到地面的高度约为()( )
A.199.1cm B.201.1cm C.200.5cm D.218.9cm
二、多选题
9.下列函数中,既是偶函数又存在零点的是( )
A. B. C. D.
10.用下列,能表示向量的是( )
A., B.,
C., D.,
11.已知双曲线的离心率为,则( )
A.的焦点在轴上 B.的虚轴长为2
C.直线与相交的弦长为1 D.的渐近线方程为
12.对于无穷数列,给出如下三个性质:①;②,;③,,,定义:同时满足性质①和②的数列为“s数列”,同时满足性质①和③的数列为“t数列”,则下列说法正确的是( )
A.若,则为“s数列”
B.若,则为“t数列”
C.若为“s数列”,则为“t数列”
D.若等比数列为“t数列”,则为“s数列”
三、填空题
13.若展开式中的系数为,则______.
14.圆有4个点到直线的距离为,则实数a的范围为_____
15.设θ为第二象限角,若tan(θ+)=,则sinθ+cosθ=_________.
16.已知过点与曲线()相切的直线有且仅有两条,则实数的取值范围是__________.
四、解答题
17.在中,角A,B,C的对边分别为a,b,c,点M在边上,是角A的平分线,,.
(1)求A;
(2)若,求的长.
18.在①,,是公差为的等差数列,②,这两个条件中任选一个,补充在下面问题中并解答.
问题:已知数列是等比数列,且满足________.
(1)求数列的通项公式;
(2)设,为数列的前n项和,证明:.
注:如果选择多个条件分别解答,按第一个解答计分.
19.如图,几何体为直四棱柱截去一个角所得,四边形是菱形,,,,P为的中点.
(1)证明:平面平面;
(2)求平面与平面所成锐二面角的余弦值.
20.已知椭圆E:的两个焦点与短轴的一个端点是等边三角形的三个顶点且长轴长为4.
求椭圆E的方程:
Ⅱ若A是椭圆E的左顶点,经过左焦点F的直线1与椭圆E交于C,D两点,求与的面积之差的绝对值的最大值为坐标原点
21.在政府精准扶贫政策的扶持下,甲、乙,丙三位学徒跟老李师傅学习制作某种陶器,经过一段时间的学习后,他们各自能制作成功该陶器的概率分别为,,,且.现需要他们三人制作一件该陶器,每次只有一个人制作,且每个人只制作一次,如果有一个人制作失败则换下一个人重新制作,若陶器制作成功则结束.
(1)按照甲、乙、丙的顺序制作该陶器,若,且,求制作该陶器的人数均值的最大值;
(2)若这种陶器制作成功后需要两轮检测都合格才能上市销售,已知学徒甲制作的陶器第一轮检测合格的概率为,第二轮检测合格的概率为,且两轮检测是否合格相互之间没有影响.如果这种陶器可以上市销售,则每件陶器可获利100元;如果这种陶器不能上市销售,则每件陶器亏损80元.现有学徒甲制作的这种陶器4件,求这4件陶器获利220元的概率.
22.已知直线是曲线的切线.
(1)求函数的解析式;
(2)证明:方程有且仅有2个实数根.
参考答案:
1.A
2.C
3.B
4.D
5.A
6.B
7.A
8.C
9.AC
10.AB
11.BC
12.ABD
13.
14.
15.
16.
17.(1)
(2)
18.(1)
(2)证明见解析
19.(1)证明见解析
(2)
20.(I);(II)
21.(1)
(2)
22.(1)
(2)证明见解析
2024海南省高三上学期高考全真模拟卷(二)数学试题含解析: 这是一份2024海南省高三上学期高考全真模拟卷(二)数学试题含解析,文件包含Unit13WeretryingtosavetheearthSectionB3a-Selfcheckpptx、核心素养目标人教版初中英语九年级全册Unit13WeretryingtosavetheearthSectionB3a-Selfcheck教案docx、核心素养目标人教版初中英语九年级全册Unit13WeretryingtosavetheearthSectionB3a-Selfcheck同步练习docx、HwVideoEditor_2021_04_12_233133681mp4等4份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
海南省2023届高三高考全真模拟卷(八)数学试题(原卷版): 这是一份海南省2023届高三高考全真模拟卷(八)数学试题(原卷版),共6页。试卷主要包含了考查范围等内容,欢迎下载使用。
海南省2023届高三高考全真模拟卷(八)数学试题(解析版): 这是一份海南省2023届高三高考全真模拟卷(八)数学试题(解析版),共23页。试卷主要包含了考查范围等内容,欢迎下载使用。












