专题3.2第一次月考阶段性测试卷02（3月培优卷，八下人教16-17章）-八年级数学下学期复习备考高分秘籍人教版

这是一份专题3.2第一次月考阶段性测试卷02（3月培优卷，八下人教16-17章）-八年级数学下学期复习备考高分秘籍人教版，文件包含专题32第一次月考阶段性测试卷023月培优卷八下人教16-17章-八年级数学下学期复习备考高分秘籍解析版人教版docx、专题32第一次月考阶段性测试卷023月培优卷八下人教16-17章-八年级数学下学期复习备考高分秘籍原卷版人教版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。
八年级数学下学期复习备考高分秘籍人教版
专题3.2第一次月考阶段性测试卷02（3月培优卷，八下人教16-17章）
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2022秋•泉港区期末）要使二次根式有意义，x的值可以是（　　）
A．﹣1 B．0 C．2 D．4
【分析】二次根式的被开方数大于等于零，由此计算解答．
【解析】解：∵x﹣3≥0，
∴x≥3，
观察只有D选项符合，
故选：D．
2．（2022秋•郴州期末）下列计算正确的是（　　）
A． B．
C． D．
【分析】由二次根式的加减运算可判断A，C，由二次根式的化简可判断B，D，从而可得答案．
【解析】解：，不是同类二次根式，不能合并，故A不符合题意；
，故B不符合题意；
，故C符合题意；
，故D不符合题意；
故选C．
3．（2022秋•平度市期末）下列各式：①，②，③，④，最简二次根式有（　　）
A．1个 B．2个 C．3个 D．4个
【分析】根据最简二次根式的定义逐个判断即可．
【解析】解：①＝，不是最简二次根式；
②，是最简二次根式；
③＝3，不是最简二次根式；
④＝，不是最简二次根式，
最简二次根式有②；
故选：A．
4．（2022秋•宝山区期末）如果y＝，则x+y的值为（　　）
A． B．1 C． D．0
【分析】直接利用二次根式有意义的条件得出x，y的值，进而得出答案．
【解析】解：∵3﹣2x≥0，2x﹣3≥0，
则x≥，x≤，
解得：x＝，
故y＝0，
则x+y＝+0＝．
故选：A．
5．（2022秋•万州区期末）若a、b、c为三角形的三边，则下列各组数据中，不能组成直角三角形的是（　　）
A．a＝3，b＝4，c＝5 B．a＝6，b＝8，c＝10
C． D．
【分析】欲判断能否构成直角三角形，只需验证两小边的平方和是否等于最长边的平方．
【解析】解：A、32+42＝52，能构成直角三角形；
B、62+82＝102，能构成直角三角形；
C、（）2+（）2≠（）2，不能构成直角三角形；
D、12+12＝（）2，能构成直角三角形．
故选：C．
6．（2022秋•福清市期末）如图，一棵垂直于地面的树在一次强台风中从高地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为（　　）

A．4.5米 B．6米 C．米 D．9米
【分析】根据含有30°角的直角三角形的性质可以得到AC的长，然后即可计算出AB+AC的值，从而可以得到这棵树在折断前的高度．
【解析】解：∵AB＝3，∠ACB＝30°，∠ABC＝90°，
∴AC＝6，
∴这棵树在折断前的高度为AC+AB＝6+3＝9（米）．
故选：D．

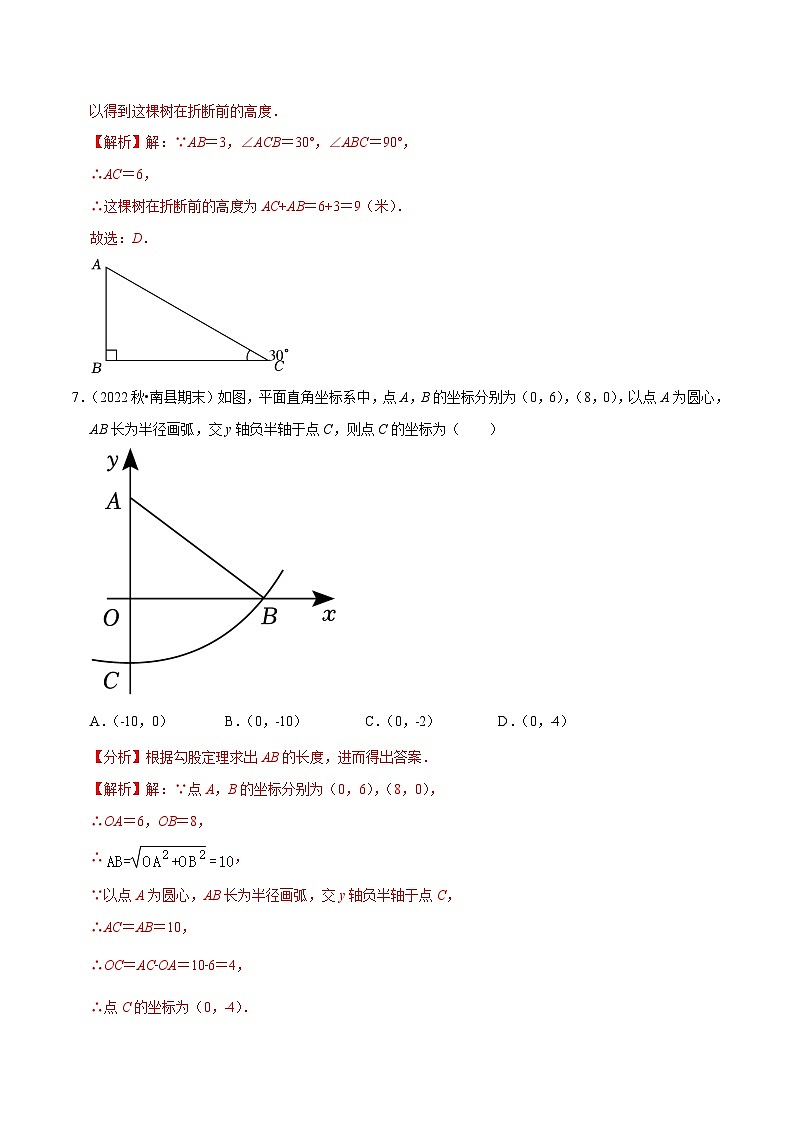
7．（2022秋•南县期末）如图，平面直角坐标系中，点A，B的坐标分别为（0，6），（8，0），以点A为圆心，AB长为半径画弧，交y轴负半轴于点C，则点C的坐标为（　　）

A．（﹣10，0） B．（0，﹣10） C．（0，﹣2） D．（0，﹣4）
【分析】根据勾股定理求出AB的长度，进而得出答案．
【解析】解：∵点A，B的坐标分别为（0，6），（8，0），
∴OA＝6，OB＝8，
∴，
∵以点A为圆心，AB长为半径画弧，交y轴负半轴于点C，
∴AC＝AB＝10，
∴OC＝AC﹣OA＝10﹣6＝4，
∴点C的坐标为（0，﹣4）．
故选：D．
8．（2023•龙川县校级开学）直角三角形的两边长m，n满足，则第三边长是（　　）
A．5 B．5或 C．4或 D．4
【分析】利用非负数的性质求出m，n，再分两种情况根据勾股定理即可解决问题．
【解析】解：∵，
∴（m﹣3）2+＝0．
∴m﹣3＝0且2n﹣8＝0．
∴m＝3，n＝4．
①n＝4为斜角边时，则第三边长为：＝；
②n＝4为直角边时，则第三边长为：＝5；
综上所述，第三边长为5或．
故选：B．
9．（2023•雁塔区校级模拟）由12个有公共顶点O的直角三角形拼成的图形如图所示，∠AOB＝∠BOC＝…＝∠LOM＝30°，且点M在线段OA上．若OA＝16，则OH的长为（　　）

A．9 B． C． D．
【分析】由已知可知∠AOB＝∠BOC＝……＝∠LOM＝30°，∠ABO＝∠BCO＝……＝∠LMO＝90°，可知AB：OB：OA＝BC：OC：OB＝……＝FG：OG：OF＝1：：2，由此可求出OH的长．
【解析】解：由图可知，∠ABO＝∠BCO＝……＝∠LMO＝90°，
∵∠AOB＝∠BOC＝……＝∠LOM＝360°÷12＝30°，
∴∠A＝∠OBC＝∠OCD＝……＝∠OLM＝60°，
∴AB＝OA，OB＝AB＝OA，
同理可得，OC＝OB＝（）2OA，
OD＝OC＝（）3OA，
……
OH＝OG＝（）7OA＝（）7×16＝．
故选：D．
10．（2022秋•安溪县期末）若a＝2020×2022﹣2020×2021，b＝，则a，b，c的大小关系是（　　）
A．c＞b＞a B．c＞a＞b C．b＞a＞c D．b＞c＞a
【分析】将各数进行化简，然后根据实数的大小比较法则即可求出答案．
【解析】解：a＝2020×（2022﹣2021）＝2020，b2＝20232﹣4×2022，c2＝20212+1，
∴b2＝（a+3）2﹣4（a+2）＝a2+2a+1，
c2＝（a+1）2+1＝a2+2a+2，
∴a2﹣b2＝a2﹣a2﹣2a﹣1＝﹣2a﹣1＜0，
c2﹣a2＝a2+2a+2﹣a2＝2a+2＞0，
b2﹣c2＝a2+2a+1﹣a2﹣2a﹣2＝﹣1＜0，
∴a2＜b2＜c2，
∴a＜b＜c，
故选：A．
二、填空题（本大题共6小题，每小题4分，共24分）请把答案直接填写在横线上
11．（2022秋•九江期末）如图，Rt△ABC的周长为24，∠C＝90°，且AB：AC＝5：4，则BC的长为 　6　．

【分析】令AB＝5x，AC＝4x，由勾股定理得到BC＝3x，由Rt△ABC的周长为24，列出关于x的方程，求出x即可求出BC长．
【解析】解：∵AB：AC＝5：4，
∴令AB＝5x，AC＝4x，
∵△ABC是直角三角形，
∴BC＝＝＝3x，
∵Rt△ABC的周长为24，
∴5x+4x+3x＝24，
∴x＝2，
∴BC＝3x＝6．
故答案为：6．
12．（2022秋•海口期末）已知﹣1＜x＜3，化简：﹣|x+1|＝　﹣2x+2　．
【分析】根据二次根式的性质和绝对值的性质求解即可．
【解析】解：∵﹣1＜x＜3，
∴﹣|x+1|
＝3﹣x﹣（x+1）
＝﹣2x+2，
故答案为：﹣2x+2．
13．（2022秋•巴中期末）计算的结果是 　1　．
【分析】利用积的乘方的逆运算及平方差公式，二次根式的相应的运算对式子进行求解即可．
【解析】解：
＝
＝
＝（3﹣4）2022
＝（﹣1）2022
＝1，
故答案为：1．
14．（2022秋•鼓楼区校级期末）如图，Rt△ABC中，∠C＝90°，∠B＝30°，∠BAC的平分线AD交BC于点D，CD＝，则BD的长是 　2　．

【分析】根据角平分线性质求出∠BAD的度数，根据含30度角的直角三角形性质求出AD即可得BD．
【解析】解：∵∠C＝90°，∠B＝30°，
∴∠CAB＝60°，
AD平分∠CAB，
∴∠BAD＝30°，
∴BD＝AD＝2CD＝2，
故答案为：2．
15．（2022秋•巴州区期末）我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”．如图是由弦图变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNPQ的面积分别为S1，S2，S3，若S1+S2+S3＝45，则S2的值是 　15　．

【分析】根据正方形的面积和勾股定理即可求解．
【解析】解：设全等的直角三角形的两条直角边为a、b且a＞b，
由题意可知：，
因为S1+S2+S3＝45，即（a+b）2+a2+b2+（a﹣b）2＝453（a2+b2）＝21，
所以3S2＝45，
∴S2的值是15．
故答案为：15．
16．（2022秋•晋州市期末）使用手机支付宝付款时，常常需要用到密码．嘉淇学完二次根式后，突发奇想，决定用“二次根式法”来产生密码．如，对于二次根式，计算结果为13，中间加一个大写字母X，就得到一个六位密码“169X13”．按照这种产生密码的方法，则利用二次根式产生的六位密码是 　121X11　．
【分析】先求出的值，再根据题意即可得出结论．
【解析】解：∵，
∴产生的六位数密码是121X11，
故答案为：121X11．
三、解答题（本大题共7小题，共66分．解答时应写出文字说明、证明过程或演算步骤）
17．（2022秋•晋州市期末）（1）计算：；
（2）计算：．
【分析】（1）根据二次根式的混合运算计算即可；
（2）利用平方差公式，二次根式的混合运算计算即可．
【解析】解：（1）
＝
＝
＝；
（2）
＝
＝5﹣2
＝3．
18．（2022秋•裕华区期末）如图，把一块直角三角形ABC（其中∠ACB＝90°）土地划出一个△ADC后，测得CD＝3米，AD＝4米，BC＝12米，AB＝13米．
（1）根据条件，求AC的长度：
（2）判断△ACD的形状，并说明理由．
（3）图中阴影部分土地的面积是 　24　平方米．

【分析】（1）利用勾股定理即可求解；
（2）利用勾股定理的逆定理判断△ACD是直角三角形；
（3）由S阴影＝S△ABC﹣S△ACD，结合三角形面积公式解答．
【解析】解：（1）∵∠ACB＝90°，BC＝12米，AB＝13米，
∴（米）；
（2）△ACD是直角三角形，
理由：∵CD＝3米，AD＝4米，AC＝5米
∴AD2+CD3＝AC2＝25，
∴∠ADC＝90°，
∴△ACD是直角三角形；
（3）S阴影＝S△ABC﹣S△ACD
＝
＝
＝30﹣6
＝24（平方米）．
故答案为：24．
19．（2022秋•江都区期末）看着冉冉升起的五星红旗，你们是否想过旗杆到底有多高呢？某数学兴趣小组为了测量旗杆高度，进行以下操作：如图1，先将升旗的绳子拉到旗杆底端，发现绳子末端刚好接触到地面；如图2，再将绳子末端拉到距离旗杆8m处，发现绳子末端距离地面2m．请根据以上测量情况，计算旗杆的高度．

【分析】根据题意画出示意图，设旗杆高度为xm，可得AC＝AD＝xm，AB＝（x﹣2）m，BC＝8m，在Rt△ABC中利用勾股定理可求出x．
【解析】解：设旗杆高度为xm，则AC＝AD＝xm，AB＝（x﹣2）m，BC＝8m，
在Rt△ABC中，
AB2+BC2＝AC2，即（x﹣2）2+82＝x2，
解得：x＝17，
答：旗杆的高度为17m．

20．（2022秋•郴州期末）设，．
（1）求a+b，的值；
（2）求a2﹣2ab+b2的值．
【分析】（1）利用二次根式的加减运算法则先计算二次根式的加法运算，再利用分母有理化的法则化简即可；
（2）先计算a﹣b，再利用完全平方公式进行计算即可．
【解析】解：（1）∵，，
∴
，．
（2）∵，，
∴，
∴．
21．（2022秋•宛城区校级期末）已知：如图，在Rt△ABC中，∠ACB＝90°，AB＝5cm，AC＝3cm，动点P从点B出发沿射线BC以2cm/s的速度移动，设运动的时间为ts．

（1）求BC边的长；
（2）当△ABP为直角三角形时，求t的值．

【分析】（1）利用勾股定理求解即可得；
（2）先求出BP＝2tcm，再分①当∠APB＝90°，②当∠BAP＝90°两种情况，利用勾股定理求解即可得．
【解析】解：（1）在Rt△ABC中，∠ACB＝90°，AB＝5cm，AC＝3cm，
由勾股定理得；
（2）由题意知BP＝2tcm．
①当∠APB＝90°时，如图，点P与点C重合，BP＝BC＝4cm，

∴t＝4÷2＝2；
②当∠BAP＝90°时，如图2，CP＝BP﹣BC＝（2t﹣4）cm，AC＝3cm．

在Rt△ACP中，AP2＝AC2+CP2＝32+（2t﹣4）2，
在Rt△BAP中，AP2＝BP2﹣AB2＝（2t）2﹣52，
因此32+（2t﹣4）2＝（2t）2﹣52，
解得．
综上所述，当△ABP为直角三角形时，t的值为2或．
22．（2022秋•道县期末）阅读下列解题过程：，，
请回答下列问题：
（1）观察上面的解答过程，请写出＝　10﹣3　；
（2）请你用含n（n为正整数）的关系式表示上述各式子的变形规律；
（3）利用上面的解法，请化简：．
【分析】观察所给例子得出（1）（2）答案；运用（2）的答案先对（3）的每项化简去掉分母，再把中间相邻的两项两两相消得到（3）的答案．
【解析】解：（1）＝
＝﹣
＝；
故答案为：．
（2）观察前面例子的过程和结果得：；
（3）反复运用得
＝
＝
＝
＝﹣1+10
＝9．
23．（2022春•大观区校级期中）阅读理解：
【问题情境】
教材中小明用4张全等的直角三角形纸片拼成图1，利用此图，可以验证勾股定理吗？
【探索新知】
从面积的角度思考，不难发现：
大正方形的面积＝小正方形的面积+4个直角三角形的面积．
从而得数学等式：（a+b）2＝c2+4×ab，化简证得勾股定理：a2+b2＝c2．
【初步运用】
（1）如图1，若b＝2a，则小正方形面积：大正方形面积＝　5：9　；
（2）现将图1中上方的两直角三角形向内折叠，如图2，若a＝4，b＝6，此时空白部分的面积为　28　；

（3）如图3，将这四个直角三角形紧密地拼接，形成风车状，已知外围轮廓（实线）的周长为24，OC＝3，求该风车状图案的面积．
（4）如图4，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3＝40，则S2＝　　．
【迁移运用】
如果用三张含60°的全等三角形纸片，能否拼成一个特殊图形呢？
带着这个疑问，小丽拼出图5的等边三角形，你能否仿照勾股定理的验证，发现含60°的三角形三边a、b、c之间的关系，写出此等量关系式及其推导过程．
知识补充：
如图6，含60°的直角三角形，对边y：斜边x＝定值k．
【分析】【初步运用】（1）如图1，求出小正方形的面积，大正方形的面积即可．
（2）根据空白部分的面积＝小正方形的面积﹣2个直角三角形的面积计算即可．
（3）可设AC＝x，根据勾股定理列出方程可求x，再根据直角三角形面积公式计算即可求解；
（4）根据图形的特征得出四边形MNKT的面积设为x，将其余八个全等的三角形面积一个设为y，从而用x，y表示出S1，S2，S3，得出答案即可．
【迁移运用】根据大正三角形面积＝三个全等三角形面积+小正三角形面积，构建关系式即可．
【解析】解：【初步运用】（1）由题意：b＝2a，c＝a，
∴小正方形面积：大正方形面积＝5a2：9a2＝5：9，
故答案为：5：9．
（2）空白部分的面积为＝52﹣2××4×6＝28．
故答案为：28．
（3）24÷4＝6，
设AC＝x，依题意有
（x+3）2+32＝（6﹣x）2，
解得x＝1，
×（3+1）×3×4
＝×4×3×4
＝24．
故该飞镖状图案的面积是24．
（4）将四边形MTKN的面积设为x，将其余八个全等的三角形面积一个设为y，
∵正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，S1+S2+S3＝40，
∴S1＝8y+x，S2＝4y+x，S3＝x，
∴S1+S2+S3＝3x+12y＝40，
∴x+4y＝，
∴S2＝x+4y＝．
故答案为：．
[迁移运用]结论：a2+b2﹣ab＝c2．
理由：由题意：大正三角形面积＝三个全等三角形面积+小正三角形面积
可得：（a+b）×k（a+b）＝3××b×ka+×c×ck，
∴（a+b）2＝3ab+c2
∴a2+b2﹣ab＝c2．