










数学3 多项式与多项式相乘教学课件ppt
展开3.多项式与多项式相乘
【基本目标】
1.能说出多项式与多项式相乘的法则,并且知道多项式乘以多项式的结果仍然是多项式.会进行多项式乘以多项式的计算及混合运算.
2.培养学生灵活运用所学知识分析问题、解决问题的能力.
3.培养独立思考、主动探索的习惯和初步解决问题的愿望及能力.
【教学重点】
掌握多项式乘以多项式的法则.
【教学难点】
运用法则进行混合运算时,不要漏项.
一、复习旧知,导入新课
指名学生说出单项式与多项式相乘的法则.(单项式乘以多项式就是用单项式乘以多项式中的每一项,再把所得的的积相加.)
式子p(a+b)=pa+pb中的p,可以是单项式,也可以是多项式.如果p=m+n,那么p(a+b)就成了(m+n)(a+b),这就是今天我们所要讲的多项式与多项式相乘的问题.(由此引出课题)
你会计算这个式子吗?你是怎样计算的?
二、师生互动,探究新知
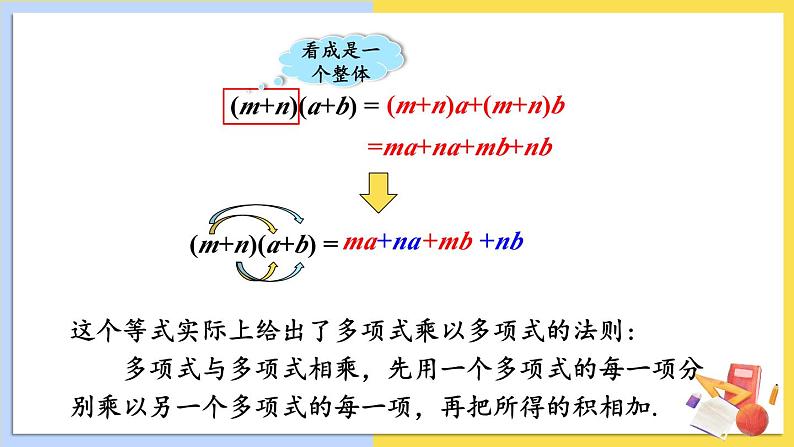
【教师活动】(教师引导学生由繁化简,把(m+n)看作一个整体,使之转化为单项式乘以多项式,即:[(m+n)(a+b)]=(m+n)a+(m+n)b=ma+mb+na+nb.
【教师活动】教材P28例图你会验证吗?
【教师活动】问题:(1)如何表示扩大后的林区的面积?
(2)用不同的方法表示出来后的等式为什么是相等的呢?
【学生活动】学生分组讨论,相互交流得出答案.
【教师活动】观察这一结果的每一项与原来两个多项式各项之间的关系,能不能由原来的多项式各项之间相乘直接得到?如果能得到,又是怎样相乘得到的?(教师示范)
1.你能用语言叙述这个式子吗?
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
即:(m+n)(a+b)=ma+mb+na+nb.
2.两个多项式相乘,不先计算能知道结果中(合并同类项前)有几项吗?
3.在计算中怎样才能不重不漏?
这个法则,对于三个或三个以上的多项式相乘,是否适用?若适用,应怎样计算?
【学生活动】学生小组讨论、交流、发言汇报.
三、随堂练习,巩固新知
完成练习册中本课时对应的课后作业部分,教师巡视,并及时反馈,特别是漏乘现象.
四、典例精析,拓展新知
例甲、乙二人共同计算一道整式乘法:(2x+a)·(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10;由于乙漏抄了第二个多项式中x的系数,得到的结果为2x2-9x+10.
(1)你能知道式子中a、b的值各是多少吗?
(2)请你计算出这道整式乘法的正确结果.
【分析】甲抄错了a的符号,即甲的计算式为(2x-a)(3x+b)=6x2-(3a-2b)x-ab.对比得到的结果可得-(3a-2b)=11;乙漏抄了第二个多项式中x的系数,即乙的计算式为(2x+a)(x+b)=2x2+(a+2b)x+ab.对比得到的结果可得出a,b的值.
解:(1)(2x-a)(3x+b)=6x2-(3a-2b)x-ab=6x2+11x-10.
(2)(2x+a)(x+b)=2x2+(a+2b)x+ab=2x2-9x+10.
∴-(3a-2b)=11,
a+2b=-9,解得a=-5,
b=-2.
(2)原式=(2x-5)(3x-2)=6x2-19x+10.
五、运用新知,深化理解
若多项式(x2+mx+n)(x2-3x+4)展开后不含x3项和x2项,试求m、n的值.
解:原式=x4+mx3+nx2-3x3-3mx2-3nx+4x2+4mx+4n=x4+(m-3)x3+(n-3m+4)x2+(4m-3n)x+4n,由题意得:
m-3=0,且n-3m+4=0
∴m=3,n=5.
【教学说明】教师提示各项系数对应,即待定系数法.
六、师生互动,课堂小结
这节课你学到了什么?有何收获?有何困惑?与同伴交流,在学生交流发言的基础上教师归纳总结.
完成练习册中本课时对应的课后作业部分.
本节课推导多项式乘多项式法则时,从单项式乘多项式法则入手,用换元思想直接推导,思维有根基,为防止本节课中最大错误——漏乘现象,教师设置了一个探究关于多项式相乘后(没合并同类项前)的项数问题,很好的避免了这个错误.典例精析中的待定系数法初次接触,注意对学习困难的学生进行及时指导.
人教版八年级上册14.1.4 整式的乘法优质ppt课件: 这是一份人教版八年级上册14.1.4 整式的乘法优质ppt课件,文件包含人教版初中数学八年级上册14142多项式与多项式相乘课件pptx、人教版初中数学八年级上册14142多项式与多项式相乘分层练习docx、人教版初中数学八年级上册14142多项式与多项式相乘教案docx、人教版初中数学八年级上册14142多项式与多项式相乘预习案docx等4份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
八年级上册5 边边边课文ppt课件: 这是一份八年级上册5 边边边课文ppt课件,文件包含5边边边pptx、5边边边doc等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
华师大版八年级上册第13章 全等三角形13.1 命题、定理与证明1 命题课文内容课件ppt: 这是一份华师大版八年级上册第13章 全等三角形13.1 命题、定理与证明1 命题课文内容课件ppt,文件包含131命题定理与证明pptx、学案131命题docdoc、教学设计131命题docdoc、学案131定理与证明docdoc、教案131命题docdoc、教案131定理与证明docdoc、定理与证明flv等7份课件配套教学资源,其中PPT共28页, 欢迎下载使用。













