河南省濮阳市第三中学2022-2023学年八年级下学期期中质量检测数学试题

这是一份河南省濮阳市第三中学2022-2023学年八年级下学期期中质量检测数学试题，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
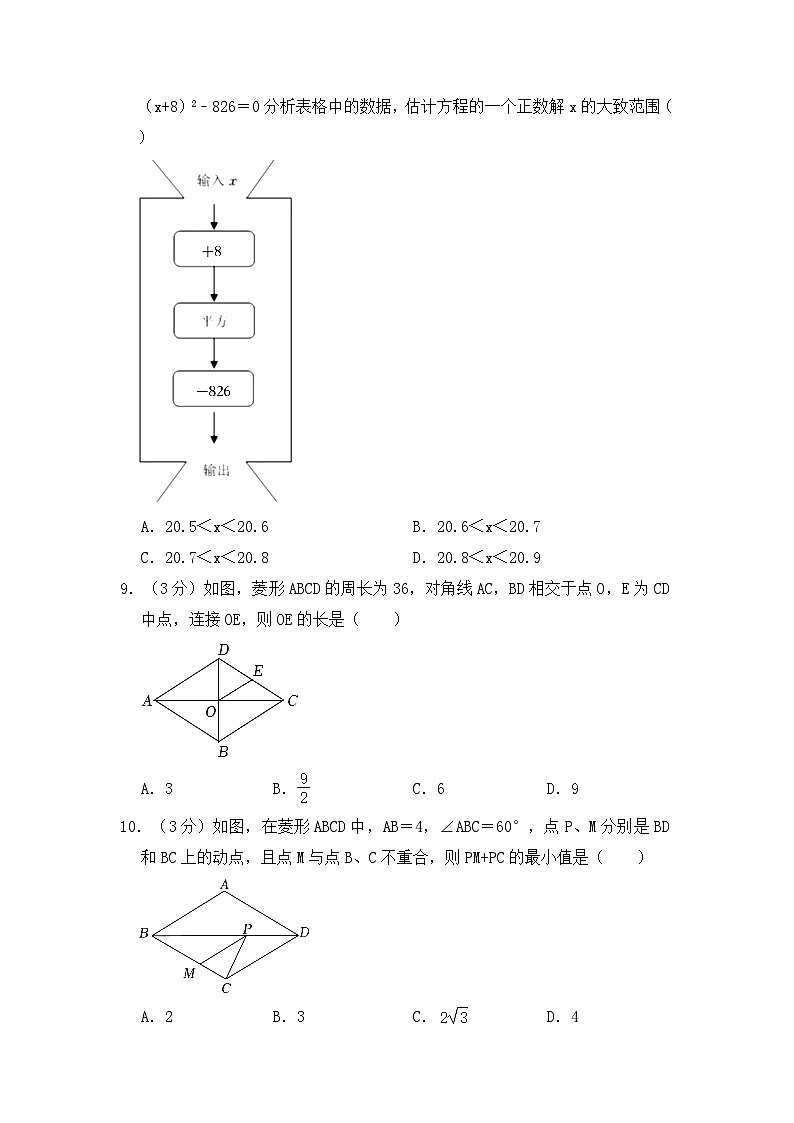
2022-2023学年河南省濮阳三中八年级（下）质检数学试卷一、选择题1．（3分）下列二次根式中，是最简二次根式的是（　　）A． B． C． D．2．（3分）下列计算正确的是（　　）A． B． C． D．3．（3分）关于x的一元二次方程x2+mx+3＝0的一个根是1，则另一个根和m的值分别为（　　）A．﹣1，3 B．1，3 C．﹣3，4 D．3，﹣44．（3分）若关于x的一元二次方程（k﹣1）x2+x+1＝0有实数根，则k的取值范围是（　　）A． B．且k≠1 C．k＜且k≠1 D．k＞5．（3分）已知a＝+，b＝，则a与b的关系是（　　）A．a＝b B．ab＝1 C．a＝﹣b D．ab＝﹣56．（3分）如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOB＝60°，BD＝8，则AB的长为（　　）A．4 B． C．3 D．57．（3分）下列命题中真命题是（　　）A．对角线互相垂直的四边形是菱形 B．矩形的四条边相等 C．对角线相等的四边形是矩形 D．菱形的对角线互相垂直8．（3分）输入一组数据，按下列程序进行计算，输出结果如表．x20.520.620.720.820.9输出﹣13.75﹣8.04﹣2.313.449.21（x+8）2﹣826＝0分析表格中的数据，估计方程的一个正数解x的大致范围（　　）A．20.5＜x＜20.6 B．20.6＜x＜20.7 C．20.7＜x＜20.8 D．20.8＜x＜20.99．（3分）如图，菱形ABCD的周长为36，对角线AC，BD相交于点O，E为CD中点，连接OE，则OE的长是（　　）A．3 B． C．6 D．910．（3分）如图，在菱形ABCD中，AB＝4，∠ABC＝60°，点P、M分别是BD和BC上的动点，且点M与点B、C不重合，则PM+PC的最小值是（　　）A．2 B．3 C． D．4二、填空题（本题共计5小题，每题3分，共计15分）11．（3分）要使代数式有意义，则x的取值范围是　             　．12．（3分）在二次根式①，②，③，④中，与是同类二次根式的有　     　（只需要填写前面的序号即可）．13．（3分）在一块长16m、宽12m的矩形土地上，要建造一个花园，使花园所占面积为矩形土地面积的一半，且花园周围的小路宽度相等，则小路的宽度为 　     　．14．（3分）a是方程2x2＝x+4的一个根，则代数式4a2﹣2a的值是　   　．15．（3分）以正方形ABCD的边AD作等边△ADE，则∠BEC的度数是　           　．三、解答题（本题共计8小题，共计75分）16．（8分）计算：（1）﹣（4﹣）；（2）（）（2﹣3÷）．17．（10分）解下列方程：（1）x2﹣5x﹣6＝0；（2）4（x﹣3）2+x（x﹣3）＝0．18．（8分）如图，在平行四边形ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E．连接BD，EC：（1）求证：四边形BECD是平行四边形；（2）若∠A＝50°，则当∠BOD＝　      　°时，四边形BECD是矩形；19．（9分）受益于国家支持新能源汽车发展和“一带一路”倡议等多重利好因素，我国某汽车零部件生产企业的利润逐年增高，据统计，2019年利润为2亿元，2021年利润为2.88亿元．（1）求该企业从2019年至2021年利润的年均增长率；（2）若2022年保持前两年利润的年均增长率不变，该企业2022年的利润能否超过3.4亿元？20．（9分）已知关于x的一元二次方程x2﹣（2m﹣3）x+m2＝0有两个不相等的实数根．（1）求m的取值范围；（2）若此方程的两实数根x1，x2满足（x1﹣1）（x2﹣1）＝7，求m的值．21．（10分）如图△ABC，∠B＝90°，AB＝6，BC＝8．点P从A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动．如果P、Q分别从A、B同时出发，当点Q运动到点C时，两点停止运动，问：（1）经过几秒，△PBQ的面积等于8cm2？（2）△PBQ的面积会等于10cm2吗？若会，请求出此时的运动时间；若不会，请说明理由．22．（10分）阅读理解阅读下列材料，然后解答问题：在进行二次根式的化简与运算时，我们有时会碰上如：，，一样的式子，其实我们还可以将其进一步化简：＝＝；（一）＝＝；（二）＝＝＝﹣1；（三）以上这种化简的步骤叫做分母有理化．还可以用以下方法化简：＝＝＝＝﹣1．（四）请解答下列问题：（1）化简：；（2）化简：++；（3）猜想：+++…+的值．（直接写出结果）23．（11分）下面是一种类比、拓展的探究案例，先阅读再解决后面的问题：已知正方形ABCD，点M在是直线BC上一个动点，点N在直线DC上，且满足∠MAN＝45°，连接MN．（1）如图1，当点M在边BC上时，求证：MN＝BM+DN．请根据下面的思路分析填空：延长线段CD至点E，使得DE＝BM，连接AE，根据正方形性质和作图可证△ABM≌　       　，得到AM＝AE，接着可证明△AMN≌　       　，可得出MN＝　     　，再由线段的加法可以得出MN＝BM+DN．（2）如图2，当点M在边CB的延长线上，点N在DC的延长线上；①猜想BM，DN，MN之间有怎样的数量关系？并证明你的猜想．②若BC＝4，BM＝1，求CN．
参考答案一、选择题（本题共计10小题，每题3分，共计30分）1．（3分）下列二次根式中，是最简二次根式的是（　　）A． B． C． D．【分析】直接利用最简二次根式的定义分析得出答案．解：A、＝3，故此选项错误；B、无法化简，故此选项正确；C、＝|x|，故此选项错误；D、＝＝，故此选项错误；故选：B．【点评】此题主要考查了最简二次根式，正确把握定义是解题关键．2．（3分）下列计算正确的是（　　）A． B． C． D．【分析】根据二次根式的加法法则，二次根式的减法法则，二次根式的乘法法则，二次根式的除法法则进行计算，再得出选项即可．解：A．和不能合并，故本选项不符合题意；B．2﹣＝，故本选项符合题意；C．÷＝＝＝2，故本选项不符合题意；D．×＝＝3，故本选项不符合题意；故选：B．【点评】本题考查了二次根式的混合运算，能正确根据二次根式的运算法则进行计算是解此题的关键．3．（3分）关于x的一元二次方程x2+mx+3＝0的一个根是1，则另一个根和m的值分别为（　　）A．﹣1，3 B．1，3 C．﹣3，4 D．3，﹣4【分析】设方程的另一个根为t，根据根与系数的关系得1+t＝﹣m，1×t＝3，然后求出t，再计算m的值．解：设方程的另一个根为t，根据根与系数的关系得1+t＝﹣m，1×t＝3，解得t＝3，m＝﹣4，即另一个根为3，m的值为﹣4．故选：D．【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．4．（3分）若关于x的一元二次方程（k﹣1）x2+x+1＝0有实数根，则k的取值范围是（　　）A． B．且k≠1 C．k＜且k≠1 D．k＞【分析】利用一元二次方程的定义和根的判别式的意义得到k﹣1≠0且Δ＝12﹣4（k﹣1）≥0，然后求出两不等式的公共部分即可．解：根据题意得k﹣1≠0且Δ＝12﹣4（k﹣1）≥0，解得k≤且k≠1．故选：B．【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根．5．（3分）已知a＝+，b＝，则a与b的关系是（　　）A．a＝b B．ab＝1 C．a＝﹣b D．ab＝﹣5【分析】根据平方差公式，可分母有理化，根据实数的大小比较，可得答案．解：b＝＝＝+，a＝+，故选：A．【点评】本题考查了分母有理化，利用平方差公式将分母有理化是解题关键．6．（3分）如图，矩形ABCD中，对角线AC，BD交于点O．若∠AOB＝60°，BD＝8，则AB的长为（　　）A．4 B． C．3 D．5【分析】先由矩形的性质得出OA＝OB，再证明△AOB是等边三角形，得出AB＝OB＝4即可．解：∵四边形ABCD是矩形，∴OA＝AC，OB＝BD＝4，AC＝BD，∴OA＝OB，∵∠AOB＝60°，∴△AOB是等边三角形，∴AB＝OB＝4；故选：A．【点评】本题考查了矩形的性质、等边三角形的判定与性质；熟练掌握矩形的性质，证明三角形是等边三角形是解决问题的关键．7．（3分）下列命题中真命题是（　　）A．对角线互相垂直的四边形是菱形 B．矩形的四条边相等 C．对角线相等的四边形是矩形 D．菱形的对角线互相垂直【分析】根据菱形、矩形的性质定理和判定定理逐项判断．解：A、对角线互相垂直的平行四边形是菱形，故A是假命题，不符合题意；B、菱形的四条边相等，故B是假命题，不符合题意；C、对角线相等的平行四边形是矩形，故C是假命题，不符合题意；D、菱形的对角线互相垂直，故D是真命题，符合题意故选：D．【点评】本题考查菱形、矩形的性质及判定，解题的关键是掌握菱形、矩形的性质定理和判定定理．8．（3分）输入一组数据，按下列程序进行计算，输出结果如表．x20.520.620.720.820.9输出﹣13.75﹣8.04﹣2.313.449.21（x+8）2﹣826＝0分析表格中的数据，估计方程的一个正数解x的大致范围（　　）A．20.5＜x＜20.6 B．20.6＜x＜20.7 C．20.7＜x＜20.8 D．20.8＜x＜20.9【分析】利用表中的对应值得到x＝20.7时，（x+8）2﹣826＝﹣2.31＜0；当x＝20.8时，（x+8）2﹣826＝3.44＞0，所以当x在20.7～20.8之间取某一个数时，（x+8）2﹣826＝0，从而根据一元二次方程解的定义可得到方程的一个正数解x的大致范围．解：∵当x＝20.7时，（x+8）2﹣826＝﹣2.31；当x＝20.8时，（x+8）2﹣826＝3.44，∴当x在20.7～20.8之间取某一个数时，（x+8）2﹣826＝0，∴估计方程的一个正数解x的大致范围为20.7＜x＜20.8．故选：C．【点评】本题考查了估算一元二次方程的近似解：给出一些未知数的值，计算方程两边结果，当两边结果愈接近时，说明未知数的值愈接近方程的根．9．（3分）如图，菱形ABCD的周长为36，对角线AC，BD相交于点O，E为CD中点，连接OE，则OE的长是（　　）A．3 B． C．6 D．9【分析】由菱形的性质可先求得菱形的边长，再由三角形中位线定理可求得OE的长．解：∵菱形ABCD的周长为36，∴CD＝BC＝＝9，且O为BD的中点，∵E为CD的中点，∴OE为△BCD的中位线，∴OE＝CB＝，故选：B．【点评】本题主要考查菱形的性质，掌握菱形的四条边都相等、对角线互相垂直平分是解题的关键．10．（3分）如图，在菱形ABCD中，AB＝4，∠ABC＝60°，点P、M分别是BD和BC上的动点，且点M与点B、C不重合，则PM+PC的最小值是（　　）A．2 B．3 C． D．4【分析】连接AC，过点A作AM⊥BC，垂足为M，交BD于点P，根据菱形的性质可得BD垂直平分AC，从而可得PA＝PC，则PC+PM＝PA+PM，当A，P，M三点共线，且AM⊥BC时，PC+PM有最小值，然后在Rt△ABM中，进行计算即可解答．解：连接AC，过点A作AM⊥BC，垂足为M，交BD于点P， ∵四边形ABCD是菱形，∴BD垂直平分AC，∴PA＝PC，∴PC+PM＝PA+PM＝AM，此时PM+PC有最小值，在Rt△ABM中，AB＝4，∠ABC＝60°，∴∠BAM＝90°﹣∠ABC＝30°，∴BM＝AB＝2，∴AM＝BM＝2，∴PM+PC的最小值是2，故选：C．【点评】本题考查了菱形的性质，轴对称﹣最短路线问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．二、填空题（本题共计5小题，每题3分，共计15分）11．（3分）要使代数式有意义，则x的取值范围是　﹣2≤x＜3且x＞3　．【分析】根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．解：由代数式有意义，得．解得﹣2≤x＜3且x＞3，故答案为：﹣2≤x＜3且x＞3．【点评】本题考查了二次根式有意义的条件，函数自变量的范围一般从三个方面考虑：当函数表达式是整式时，自变量可取全体实数；当函数表达式是分式时，考虑分式的分母不能为0；当函数表达式是二次根式时，被开方数非负．12．（3分）在二次根式①，②，③，④中，与是同类二次根式的有　②④　（只需要填写前面的序号即可）．【分析】结合同类二次根式的概念：一般地，把几个二次根式化为最简二次根式后，如果它们的被开方数相同，就把这几个二次根式叫做同类二次根式．进行求解即可．解：①、＝3，与不是同类二次根式；②、＝4，与是同类二次根式；③、＝，与不是同类二次根式；④、＝，与是同类二次根式．故答案为：②④．【点评】本题考查了同类二次根式，解答本题的关键在于熟练掌握该知识点的概念：一般地，把几个二次根式化为最简二次根式后，如果它们的被开方数相同，就把这几个二次根式叫做同类二次根式．13．（3分）在一块长16m、宽12m的矩形土地上，要建造一个花园，使花园所占面积为矩形土地面积的一半，且花园周围的小路宽度相等，则小路的宽度为 　2m　．【分析】设小路的宽度为xm，则花园的长为（16﹣2x）m，宽为（12﹣2x）m，由题意：花园所占面积为矩形土地面积的一半，列出一元二次方程，解方程即可．解：设小路的宽度为xm，则花园的长为（16﹣2x）m，宽为（12﹣2x）m，由题意得：（16﹣2x）（12﹣2x）＝×16×12，整理得：x2﹣14x+24＝0，解得：x1＝2，x2＝12（不符合题意，舍去），即小路的宽度为2m，故答案为：2m．【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．14．（3分）a是方程2x2＝x+4的一个根，则代数式4a2﹣2a的值是　8　．【分析】直接把a的值代入得出2a2﹣a＝4，进而将原式变形得出答案．解：∵a是方程2x2＝x+4的一个根，∴2a2﹣a＝4，∴4a2﹣2a＝2（2a2﹣a）＝2×4＝8．故答案为：8．【点评】此题主要考查了一元二次方程的解，正确将原式变形是解题关键．15．（3分）以正方形ABCD的边AD作等边△ADE，则∠BEC的度数是　30°或150°　．【分析】分等边△ADE在正方形的内部和外部两种情况分别求解可得．解：如图1，∵四边形ABCD为正方形，△ADE为等边三角形，∴AB＝BC＝CD＝AD＝AE＝DE，∠BAD＝∠ABC＝∠BCD＝∠ADC＝90°，∠AED＝∠ADE＝∠DAE＝60°，∴∠BAE＝∠CDE＝150°，又AB＝AE，DC＝DE，∴∠AEB＝∠CED＝15°，则∠BEC＝∠AED﹣∠AEB﹣∠CED＝30°．如图2，∵△ADE是等边三角形，∴AD＝DE，∵四边形ABCD是正方形，∴AD＝DC，∴DE＝DC，∴∠CED＝∠ECD，∴∠CDE＝∠ADC﹣∠ADE＝90°﹣60°＝30°，∴∠CED＝∠ECD＝（180°﹣30°）＝75°，∴∠BEC＝360°﹣75°×2﹣60°＝150°．故答案为：30°或150°．【点评】本题考查了正方形的性质，等边三角形的性质，等腰三角形的判定与性质，熟记各性质并准确识图是解题的关键．三、解答题（本题共计8小题，共计75分）16．（8分）计算：（1）﹣（4﹣）；（2）（）（2﹣3÷）．【分析】（1）直接化简二次根式，进而合并得出答案；（2）直接利用二次根式的混合运算法则化简，进而得出答案．解：（1）原式＝2﹣3﹣（4×﹣2）＝2﹣3﹣（2﹣2）＝2﹣3﹣2+2＝﹣； （2）原式＝（+2）（2﹣﹣12÷）＝（+2）（2﹣﹣8）＝（+2）（﹣6﹣）＝﹣42﹣24．【点评】此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．17．（10分）解下列方程：（1）x2﹣5x﹣6＝0；（2）4（x﹣3）2+x（x﹣3）＝0．【分析】（1）利用因式分解法把方程转化为x﹣6＝0或x+1＝0，然后解两个一次方程即可；（2）利用因式分解法把方程转化为x﹣3＝0或4x﹣12+x＝0，然后解两个一次方程即可．解：（1）x2﹣5x﹣6＝0，（x﹣6）（x+1）＝0，x﹣6＝0或x+1＝0，所以x1＝6，x2＝﹣1；（2）4（x﹣3）2+x（x﹣3）＝0，（x﹣3）（4x﹣12+x）＝0，x﹣3＝0或4x﹣12+x＝0，所以x1＝3，x2＝．【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．18．（8分）如图，在平行四边形ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E．连接BD，EC：（1）求证：四边形BECD是平行四边形；（2）若∠A＝50°，则当∠BOD＝　100　°时，四边形BECD是矩形；【分析】（1）由AAS证明△BOE≌△COD，得出OE＝OD，即可得出结论；（2）由平行四边形的性质得出∠BCD＝∠A＝50°，由三角形的外角性质求出∠ODC＝∠BCD，得出OC＝OD，证出DE＝BC，即可得出结论．【解答】（1）证明：∵四边形ABCD为平行四边形，∴AB∥DC，AB＝CD，∴∠OEB＝∠ODC，又∵O为BC的中点，∴BO＝CO，在△BOE和△COD中，∴△BOE≌△COD（AAS），∴OE＝OD，∴四边形BECD是平行四边形；（2）解：若∠A＝50°，则当∠BOD＝100°时，四边形BECD是矩形．理由如下：∵四边形ABCD是平行四边形，∴∠BCD＝∠A＝50°，∵∠BOD＝∠BCD+∠ODC，∴∠ODC＝100°﹣50°＝50°＝∠BCD，∴OC＝OD，∵BO＝CO，OD＝OE，∴DE＝BC，∵四边形BECD是平行四边形，∴四边形BECD是矩形；故答案为：100．【点评】本题主要考查了矩形的判定、平行四边形的判定与性质、全等三角形的判定与性质等知识，熟练掌握平行四边形的判定与性质是解决问题的关键．19．（9分）受益于国家支持新能源汽车发展和“一带一路”倡议等多重利好因素，我国某汽车零部件生产企业的利润逐年增高，据统计，2019年利润为2亿元，2021年利润为2.88亿元．（1）求该企业从2019年至2021年利润的年均增长率；（2）若2022年保持前两年利润的年均增长率不变，该企业2022年的利润能否超过3.4亿元？【分析】（1）设该企业从2019年至2021年利润的年均增长率为x，根据该企业2021年的利润＝该企业2019年利润×（1+该企业从2019年至2021年利润的年均增长率）2，可得出关于x的一元二次方程，解之取其符合题意的值，即可得出结论；（2）利用该企业2022年的利润＝该企业2021年的利润×（1+该企业从2019年至2021年利润的年均增长率），可求出该企业2022年的利润，再将其与3.45亿元比较后，即可得出结论．解：（1）设该企业从2019年至2021年利润的年均增长率为x，根据题意得：2（1+x）2＝2.88，解得：x1＝0.2＝20%，x2＝﹣2.2（不符合题意，舍去）．答：该企业从2019年至2021年利润的年均增长率为20%；（2）∵2.88×（1+20%）＝3.456（亿元），3.456＞3.4，∴该企业2022年的利润能超过3.4亿元．【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．20．（9分）已知关于x的一元二次方程x2﹣（2m﹣3）x+m2＝0有两个不相等的实数根．（1）求m的取值范围；（2）若此方程的两实数根x1，x2满足（x1﹣1）（x2﹣1）＝7，求m的值．【分析】（1）利用判别式的意义得到Δ＝（2m﹣3）2﹣4m2＞0，然后解不等式即可；（2）根据根与系数的关系得到x1+x2＝2m﹣3，x1x2＝m2，再根据（x1﹣1）（x2﹣1）＝7得到m2﹣（2m﹣3）+1＝7，然后解关于m的方程，最后利用m的范围确定m的值．解：（1）根据题意得Δ＝（2m﹣3）2﹣4m2＞0，解得m＜；（2）根据题意得x1+x2＝2m﹣3，x1x2＝m2，∵（x1﹣1）（x2﹣1）＝7，∴x1x2﹣（x1+x2）+1＝7，即m2﹣（2m﹣3）+1＝7，整理得m2﹣2m﹣3＝0，解得m1＝﹣1，m2＝3，∵m＜，∴m＝﹣1．【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．也考查了根的判别式．21．（10分）如图△ABC，∠B＝90°，AB＝6，BC＝8．点P从A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动．如果P、Q分别从A、B同时出发，当点Q运动到点C时，两点停止运动，问：（1）经过几秒，△PBQ的面积等于8cm2？（2）△PBQ的面积会等于10cm2吗？若会，请求出此时的运动时间；若不会，请说明理由．【分析】（1）设经过x秒，△PBQ的面积等于8cm2．先用含x的代数式分别表示BP和BQ的长度，再代入三角形面积公式，列出方程，即可将时间求出；（2）设经过y秒，△PBQ的面积等于10cm2．根据三角形的面积公式，列出关于y的一元二次方程，根据Δ＝b2﹣4ac进行判断．解：（1）设经过x秒，△PBQ的面积等于8cm2．∵AP＝1•x＝x，BQ＝2x，∴BP＝AB﹣AP＝6﹣x，∴S△PBQ＝×BP×BQ＝×（6﹣x）×2x＝8，∴x2﹣6x+8＝0，解得：x＝2或4，即经过2秒或4秒，△PBQ的面积等于8cm2； （2）设经过y秒，△PBQ的面积等于10cm2，则S△PBQ＝×（6﹣y）×2y＝10，即y2﹣6y+10＝0，因为Δ＝b2﹣4ac＝36﹣4×10＝﹣4＜0，所以△PBQ的面积不会等于10cm2．【点评】本题考查了一元二次方程的应用．关键是用含时间的代数式准确表示BP和BQ的长度，再根据三角形的面积公式列出一元二次方程，进行求解．22．（10分）阅读理解阅读下列材料，然后解答问题：在进行二次根式的化简与运算时，我们有时会碰上如：，，一样的式子，其实我们还可以将其进一步化简：＝＝；（一）＝＝；（二）＝＝＝﹣1；（三）以上这种化简的步骤叫做分母有理化．还可以用以下方法化简：＝＝＝＝﹣1．（四）请解答下列问题：（1）化简：；（2）化简：++；（3）猜想：+++…+的值．（直接写出结果）【分析】（1）利用分母有理化的方法进行运算即可；（2）对各分母进行分母有理化运算，从而可求解；（3）对分母进行分母有理化运算，从而可求解．解：（1）＝＝＝；（2）++＝+＝＝；（3）+++…+＝+…+＝．【点评】本题主要考查二次根式的混合运算，解答的关键是理解清楚分母有理化的方法．23．（11分）下面是一种类比、拓展的探究案例，先阅读再解决后面的问题：已知正方形ABCD，点M在是直线BC上一个动点，点N在直线DC上，且满足∠MAN＝45°，连接MN．（1）如图1，当点M在边BC上时，求证：MN＝BM+DN．请根据下面的思路分析填空：延长线段CD至点E，使得DE＝BM，连接AE，根据正方形性质和作图可证△ABM≌　△ADE　，得到AM＝AE，接着可证明△AMN≌　△AEN　，可得出MN＝　EN　，再由线段的加法可以得出MN＝BM+DN．（2）如图2，当点M在边CB的延长线上，点N在DC的延长线上；①猜想BM，DN，MN之间有怎样的数量关系？并证明你的猜想．②若BC＝4，BM＝1，求CN．【分析】（1）延长线段CD至点E，使得DE＝BM，连接AE，根据正方形性质和作图可证△ABM≌△ADE（SAS），得到AM＝AE，接着可证明△AMN≌△AEN（SAS），可得出MN＝EN，再由线段的加法可以得出MN＝BM+DN；（2）①在CD上截取DF，使得DF＝BM，连接AF，由SAS证得△ABM≌△ADF，得出AM＝AF，∠BAM＝∠DAF，证明∠FAN＝∠MAN，由SAS证得△AMN≌△AFN，得出MN＝FN，即可得出MN＝DN﹣BM；②由正方形的性质得CD＝BC＝4，由①得BM＝DF＝1，则CM＝5，CF＝3，设CN＝x，由①得MN＝FN＝x+3，在Rt△MCN中，由勾股定理得CM2+CN2＝MN2，解方程即可得出结果．解：（1）延长线段CD至点E，使得DE＝BM，连接AE，∵四边形ABCD是正方形，∴AB＝AD，∠ABM＝∠ADE＝∠BAD＝90°，在△ABM和△ADE中，，∴△ABM≌△ADE（SAS），∴AM＝AE，∠BAM＝∠DAE，∵∠MAN＝45°，∴∠BAM+∠NAD＝∠BAD﹣∠MAN＝90°﹣45°＝45°，∴∠DAE+∠NAD＝45°，即∠EAN＝45°，∴∠MAN＝∠EAN，在△AMN和△AEN中，，∴△AMN≌△AEN（SAS），∴MN＝EN，∴MN＝DE+DN＝BM+DN；故答案为：△ADE，△AEN，EN；（2）①猜想BM，DN，MN之间的数量关系为：MN＝DN﹣BM；理由如下：在CD上截取DF，使得DF＝BM，连接AF，如图2所示：∵四边形ABCD是正方形，∴AB＝AD，∠ABM＝∠ADF＝∠BAD＝90°，在△ABM和△ADF中，，∴△ABM≌△ADF（SAS），∴AM＝AF，∠BAM＝∠DAF，∵∠MAN＝45°，∴∠FAN＝∠BAD﹣∠DAF﹣∠BAN＝90°﹣∠BAM﹣∠BAN＝90°﹣∠MAN＝90°﹣45°＝45°，∴∠FAN＝∠MAN，在△AMN和△AFN中，，∴△AMN≌△AFN（SAS），∴MN＝FN，∵FN＝DN﹣DF＝DN﹣BM，∴MN＝DN﹣BM；②∵四边形ABCD是正方形，∴CD＝BC＝4，由①得：BM＝DF＝1，∴CM＝BC+BM＝4+1＝5，CF＝CD﹣DF＝4﹣1＝3，设CN＝x，由①得：MN＝FN＝x+3，在Rt△MCN中，由勾股定理得：CM2+CN2＝MN2，即：52+x2＝（x+3）2，解得：x＝，即CN＝．【点评】本题是四边形综合题，主要考查了正方形的性质、全等三角形的判定与性质、勾股定理等知识；熟练掌握正方形的性质和全等三角形的判定与性质是解题的关键．