华师大版数学八年级上册 11 本章复习 PPT课件+教案

本章复习

【基本目标】

1.了解平方根、算术平方根、立方根的概念,会用根号表示.

2.了解平方与开平方，立方与开立方互为逆运算，会用平方与立方的运算求某些数的平方根与立方根.

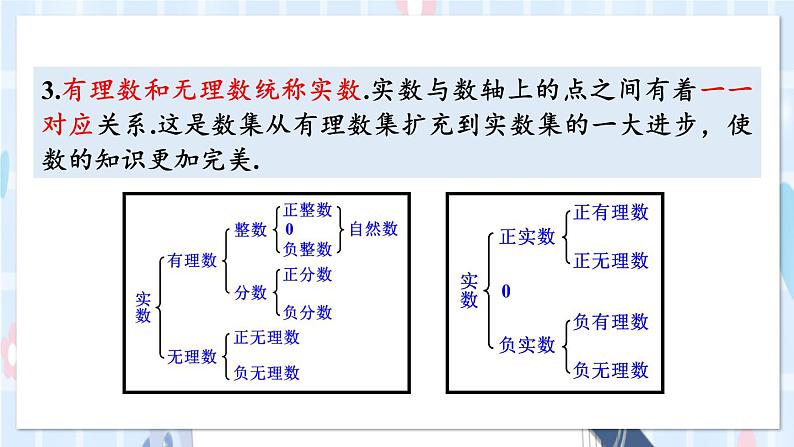
3.了解无理数的概念，知道实数与数轴上的点一一对应.

4.能进行实数的运算，会估算无理数的大小.

【教学重点】

平方根与立方根，实数及运算.

【教学难点】

实数的估算，平方根的性质.

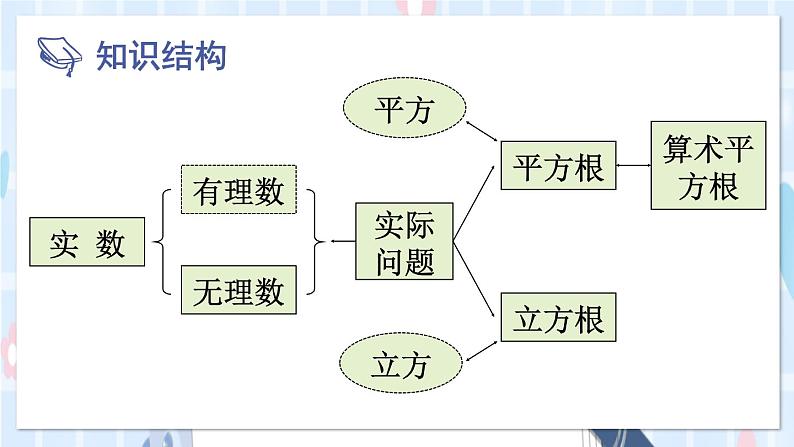
一、知识框图，整体建构

二、知识梳理，快乐晋级

本章通过问题的形式来梳理知识，以加深学生对基础知识的理解.

问题1：平方根与立方根的定义是什么？它们有什么性质？

问题2：有理数与实数的定义是什么？

问题3：数轴上的点与实数有什么关系？你是怎么理解的？

问题4：实数的相反数、绝对值、倒数与有理数相同吗？

问题5：实数运算法则、运算律与有理数相同吗？

【教学说明】教师提出问题以小组竞赛的形式回答，教师根据回答的情况，进行必要的讲解与说明，做到切中要害、言简意赅.

三、典例精析，升华旧知

例1（1）（-2）2的平方根是（     ）

A.-2

B.2

C.±2

D.±4

（2）下列说法中，正确的是（     ）

A.正数的立方根是正数

B.负数的平方根是负数

C.无理数是开方开不尽的数

D.数轴上的点只能表示有理数

（3）- 的立方根是          .

（4）81的算术平方根是          .

（5）实数a、b满足+(b-2)2=0，则ab=          .

【答案】（1）C  （2）A  （3）-5/4   （4）3   （5）-2.

【教学说明】这四道小题学生小组内自评自改.教师指出（4）中应转化为9的算术平方根，应将间接条件直接化.

例2  +1的小数部分为a，整数部分为b，求a-b的值.

【分析】∵3＜＜4，4＜+1＜5，

∴+1的整数部分b=4，小数部分b=+1-4=-3，∴a-b=（-3）-4=-7.

【教学说明】本题包含无理数的估算和无理数的运算，关键是确定+1的整数部分b的值.特别估算能力数学课程标准较重视.

例3已知实数a、b、c在数轴上的位置如图所示.

化简： -|c-a|+|a+c|.

【分析】由数轴知道b＜0,c-a＜0，a+c＞0, 表示b2的算术平方根，故原式=-b+（c-a）+（a+c）=2c-b.

【教学说明】利用数形结合，判断绝对值里面的数的正负性，其中b2的意义是解题的关键.

四、师生互动，课堂小结

这节课你有什么收获？有何疑惑？复习了哪些数学思想方法？与同伴交流.在学生交流发言的基础上，教师归纳总结.

完成练习册中本课时对应的课后作业部分.

本节复习课从知识构建到知识梳理应让学生积极自主的完成，在完成知识构建（梳理）过程中寻找薄弱环节，从而抓住复习的针对性.

典例精析部分，教师应注意根据教学的实际动态进行及时归纳，点评，让知识类化，形成能力.

在复习的过程中，学生难免有遗漏的地方，教师应以激励为主.