2023年河南省南阳市宛城区中考一模数学试题

这是一份2023年河南省南阳市宛城区中考一模数学试题，共38页。

2023年初中毕业班第一次调研测试
数学试题卷
注意事项：
1．本试卷满分120分，考试时间100分钟．
2．答题前，考生务必先将自己的姓名、考号、学校等填写在试题卷和答题卡相应的位置．
3．考生作答时，将答案涂、写在答题卡上，在本试题卷上答题无效．
4．考试结束，将答题卡和试题卷一并交回．
一、选择题：（每小题3分，共30分．）（下列各小题只有一个答案是正确的．）
1. 如果温度上升2 ℃记作 ℃，那么温度下降3 ℃记作（ ）
A. ℃ B. ℃
C. ℃ D. ℃
2. 下列几何体的三视图中没有矩形的是（　　）
A. B. C. D.
3. 多项式因式分解结果是( )
A. x（x﹣4）+4 B. （x+2）（x﹣2） C. （x+2）2 D. （x﹣2）2
4. 下列语句所描述的事件是随机事件的是（ ）
A. 两点决定一直线 B. 清明时节雨纷纷 C. 没有水分，种子发芽 D. 太阳从东方升起
5. 将一副直角三角板按如图所示的位置摆放，若，则图中∠1的度数是（ ）

A. B. C. D.
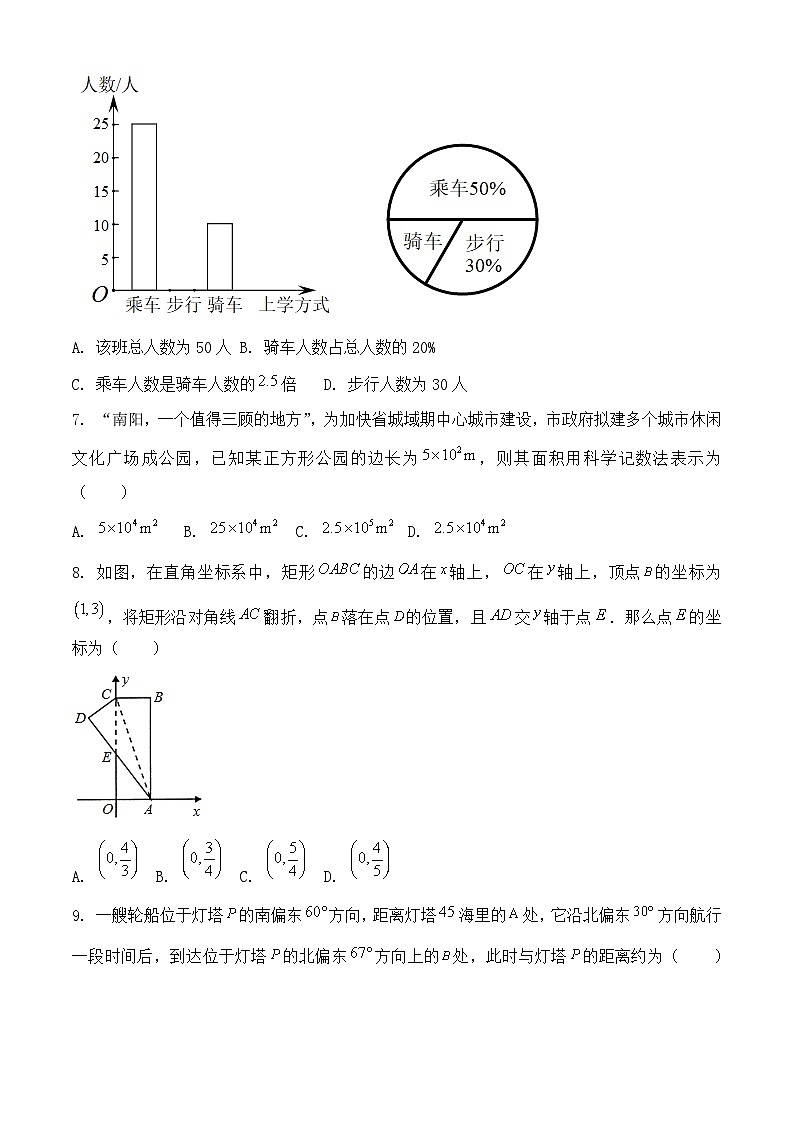
6. 下面两图是某班全体学生上学时，乘车、步行、骑车的人数分布条形统计图和扇形统计图（两图均不完整），则下列结论中错误的是（ ）

A. 该班总人数为50人 B. 骑车人数占总人数的20%
C. 乘车人数是骑车人数的倍 D. 步行人数为30人
7. “南阳，一个值得三顾的地方”，为加快省城域期中心城市建设，市政府拟建多个城市休闲文化广场成公园，已知某正方形公园的边长为，则其面积用科学记数法表示为（ ）
A. B. C. D.
8. 如图，在直角坐标系中，矩形的边在轴上，在轴上，顶点的坐标为，将矩形沿对角线翻折，点落在点的位置，且交轴于点．那么点的坐标为（ ）

A. B. C. D.
9. 一艘轮船位于灯塔的南偏东方向，距离灯塔海里的处，它沿北偏东方向航行一段时间后，到达位于灯塔的北偏东方向上的处，此时与灯塔的距离约为（ ）（参考数据：，，）

A. 海里 B. 海里 C. 海里 D. 海里
10. 观察下列等式：，，，，，，…，根据其中的规律可得的结果的个位数字是（ ）
A. B. C. D.
二、填空题（每小题3分，共15分）
11. 用一根小木棒与两根长分别为、的小木棒围成三角形，则这根小木棒的长度可以为__________（写出一个即可）
12. 若关于x的没有实数根，则k的最小整数值是___________．
13. 如图，在中，，观察尺规作图痕迹，若，则的长是______．

14. 等腰直角三角形 中， 为 上一点， ，以 为圆心， 为半径画弧交 于点 ， 交 的延长线于点 ， 则图中阴影部分面积为_______________．

15. 【实践操作】将一张直角三角形纸片沿一条直线剪掉一张三角形纸片，剩下一张如图所示的四边形纸片，其中，，，，，那么剪掉的三角形纸片的面积是___________．

三、解答题（共8个小题，满分75分）
16. 计算：
（1）；
（2）．
17. 【问题情境】大自然中的植物千姿百态，如果细心观察，就会发现：不同植物的叶子通常有着不同的特征，如果我们用数学的眼光来观察，会有什么发现呢？“数智”小组的四位同学开展了“利用树叶的特征对树木进行分类”的项目化学习活动．

【实践发现】同学们从收集的杨树叶、柳树叶中各随机选取10片，通过测量得到这些树叶的长和宽（单位：cm）的数据后，分别计算长宽比，整理数据如下：
序号
1
2
3
4
5
6
7
8
9
10
杨树叶的长宽比
2
2.4
2.1
2.4
28
1.8
2.4
2.2
2.1
1.7
柳树叶的长宽比
1.5
1.6
1.5
1.4
1.5
1.4
1.7
1.5
1.6
1.4
【实践探究】分析数据如下：

平均数
中位数
众数
方差
杨树叶的长宽比
2.19

2.4
0.0949
柳树叶的长宽比
151
1.5

0.0089
【问题解决】
（1）上述表格中：______，______；
（2）①这两种树叶从长宽比的方差来看，______树叶的形状差别较小；
②该小组收集的树叶中有一片长为11.5cm，宽为5cm的树叶，这片树叶来自于______树的可能性大；
（3）该小组准备从四位成员中随机选取两名同学进行成果汇报，请用列表或画树状图的方法求成员小颖和小娜同时被选中的概率．
18. 【阅读与思考】平移是初中几何变换之一，它可以将线段和角平移到一个新的位置，从而把分散的条件集中到一起，使问题得以解决．
【问题情景】如图1，在正方形中中，E、F、G分别是、、上的点，于点O，求证：．
小明尝试平移线段到，构造≌，使问题得到解决．

（1）【阅读理解】按照小明的思路，证明≌的依据是_______；
（2）【尝试应用】
如图2，在5×6的正方形网格中，点A、B、C、D为格点，交于点M．则的度数为_________；
（3）如图3，在正方形方格纸中，每个小正方形的边长都相等，A、B、C、D都在格点处，与相交于点P，求的值．
19. 环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mgL．环保局要求该企业立即整改，在15天以内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AB表示前3天的变化规律，其中第3天时硫化物的浓度降为4mgL．从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系：
时间x（天）
3
4
5
6
8
……
硫化物的浓y（mg/L）
4
3
2.4
2
1.5



（1）求整改过程中当0≤x＜3时，硫化物的浓度y与时间x的函数表达式；
（2）求整改过程中当x≥3时，硫化物的浓度y与时间x的函数表达式；
（3）该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0mgL？为什么？
20. 如图，是的直径，是的弦，过点作的切线，交的延长线于点，过点作于点，交的延长线于点．

（1）求证：；
（2）若，的半径是，求的长．
21. 2023春节档电影《满江红》热映，进一步激发观众爱国之情．帝都南阳与名将岳飞有着一段传颂至今的历史——公元1138年，岳飞统军过南阳到武侯祠敬拜诸葛亮，雨夜含泪手书前后《出师表》，为南阳留下了千古绝唱“三绝碑”．
某超市采购了两批同样的《出师表》纪念品挂件，第一批花了3300元，第二批花了4000元，已知第一批每个挂件的进价是第二批的倍，且第二批比第一批多购进25个．

（1）求第二批每个挂件的进价；
（2）两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？
22. 综合与实践课上，诸葛小组三位同学对含角的菱形进行了探究．
【背景】在菱形中，，作，、分别交边、于点、．

（1）【感知】如图1，若点是边的中点，小南经过探索发现了线段与之间的数量关系，请你写出这个关系式___________．
（2）【探究】如图2，小阳说“点为上任意一点时，（1）中的结论仍然成立”，你同意吗？请说明理由．
（3）【应用】小宛取出如图3所示菱形纸片，测得，，在边上取一点，连接，在菱形内部作，交于点，当时，请直接写出线段的长．
23. 如图，三孔桥横截面的三个孔都呈抛物线形，左右两个抛物线形是全等的，正常水位时，大孔水面宽度为，顶点距水面（即），小孔顶点距水面（即，建立如图所示的平面直角坐标系．

（1）求出大孔抛物线的解析式；
（2）航管部门设定警戒水位为正常水位上方处，汛期某天水位正好达到警戒水位，有一艘顶部高出水面，顶部宽的巡逻船要路过三孔桥，请问该巡逻船能否安全通过大孔？并说明理由．
（3）当水位上涨到刚好淹没小孔时，求出大孔的水面宽度．
2023年初中毕业班第一次调研测试
数学试题卷
注意事项：
1．本试卷满分120分，考试时间100分钟．
2．答题前，考生务必先将自己的姓名、考号、学校等填写在试题卷和答题卡相应的位置．
3．考生作答时，将答案涂、写在答题卡上，在本试题卷上答题无效．
4．考试结束，将答题卡和试题卷一并交回．
一、选择题：（每小题3分，共30分．）（下列各小题只有一个答案是正确的．）
1. 如果温度上升2 ℃记作 ℃，那么温度下降3 ℃记作（ ）
A. ℃ B. ℃
C. ℃ D. ℃
【答案】D
【解析】
【分析】根据正数与负数的表示方法，可得解．
详解】解：上升2℃记作℃，下降3℃记作℃；
故选：D．
【点睛】本题考查正数和负数；能够根据实际问题理解正数与负数的意义和表示方法是解题的关键．
2. 下列几何体的三视图中没有矩形的是（　　）
A. B. C. D.
【答案】D
【解析】
【分析】根据长方体、三棱柱、圆柱以及圆锥的三视图进行判断即可．
【详解】解：A．该长方体的主视图、左视图、俯视图都是矩形，
因此选项A不符合题意；
B．该三棱柱的主视图、左视图是矩形，
因此选项B不符合题意；
C．该圆柱体的主视图、左视图是矩形，
因此选项C不符合题意；
D．该圆锥的主视图、左视图是等腰三角形，俯视图是带圆心的圆、所以它的三视图没有矩形，
因此选项D符合题意；
故选：D．
【点睛】本题考查简单几何体的三视图，理解视图的意义，掌握简单几何体的三视图的形状是正确判断的前提．
3. 多项式因式分解的结果是( )
A. x（x﹣4）+4 B. （x+2）（x﹣2） C. （x+2）2 D. （x﹣2）2
【答案】D
【解析】
【分析】根据完全平方公式进行因式分解即可．
【详解】解：．
故选：D．
【点睛】本题主要考查了公式法分解因式，理解完全平方公式是解答关键．
4. 下列语句所描述的事件是随机事件的是（ ）
A. 两点决定一直线 B. 清明时节雨纷纷 C. 没有水分，种子发芽 D. 太阳从东方升起
【答案】B
【解析】
【分析】根据确定事件和随机事件的定义来区分判断即可，必然事件和不可能事件统称确定性事件；必然事件：在一定条件下，一定会发生的事件称为必然事件；不可能事件：在一定条件下，一定不会发生的事件称为不可能事件；随机事件：在一定条件下，可能发生也可能不发生的事件称为随机事件．
【详解】解：A．两点决定一直线，该事件是必然事件，故此选项不符合题意；
B．清明时节雨纷纷，该事件是随机事件，故此选项符合题意；
C．没有水分，种子发芽，该事件是不可能事件，故此选项不符合题意；
D．太阳从东方升起，该事件是必然事件，故此选项不符合题意．
故选：B．
【点睛】本题考查确定事件和随机事件的定义，熟悉定义是解题的关键．
5. 将一副直角三角板按如图所示的位置摆放，若，则图中∠1的度数是（ ）

A. B. C. D.
【答案】B
【解析】
【分析】根据平行线的性质，可得，再利用三角形的外角性质即可求出结论．
【详解】解：如图所示：与相交于点G，，

，
，
，
，
故选：B．
【点睛】本题考查的是平行线的性质，三角形的外角性质，解题的关键是熟练掌握相关的性质．
6. 下面两图是某班全体学生上学时，乘车、步行、骑车人数分布条形统计图和扇形统计图（两图均不完整），则下列结论中错误的是（ ）

A. 该班总人数为50人 B. 骑车人数占总人数的20%
C. 乘车人数是骑车人数的倍 D. 步行人数为30人
【答案】D
【解析】
【分析】此题首先根据乘车人数和所占总数的比例，求出总人数，即可根据图中获取信息求出步行的人数；根据乘车和骑车所占比例，可得乘车人数是骑车人数的2.5倍．
【详解】根据条形图可知：
乘车的人数是25人，所以总数是：25÷50%=50(人)；故A选项正确；
骑车人数在扇形图中占总人数的：1-50%-30%=20%；故B选项正确；
则乘车人数是骑车人数的2.5倍；故C选项正确；
步行人数为30%×50=15(人)，故D选项错误；
故选：D．
【点睛】本题考查了扇形统计图和条形统计图及相关计算．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．
7. “南阳，一个值得三顾的地方”，为加快省城域期中心城市建设，市政府拟建多个城市休闲文化广场成公园，已知某正方形公园的边长为，则其面积用科学记数法表示为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【详解】解：由题意可得公园的面积为：
故选：C．
【点睛】本题考查了科学记数法的表示方法，掌握形式为，其中是关键．
8. 如图，在直角坐标系中，矩形的边在轴上，在轴上，顶点的坐标为，将矩形沿对角线翻折，点落在点的位置，且交轴于点．那么点的坐标为（ ）

A. B. C. D.
【答案】A
【解析】
【分析】先证明（设），根据勾股定理列出，求得，即可解决问题．
【详解】解：设，
∵矩形沿对角线翻折，
∴，，
∴，
∴，
∴，
∵，
∴，，
∴，
在中，，
∴，
解得：，
∴，
∴点的坐标为．
故选：A．
【点睛】本题考查翻折变换性质及其应用问题．解题的关键是掌握翻折变换的性质，矩形的性质及勾股定理．
9. 一艘轮船位于灯塔的南偏东方向，距离灯塔海里的处，它沿北偏东方向航行一段时间后，到达位于灯塔的北偏东方向上的处，此时与灯塔的距离约为（ ）（参考数据：，，）

A. 海里 B. 海里 C. 海里 D. 海里
【答案】C
【解析】
【分析】由题意可得，，，则，，在中，利用正弦函数的定义求解即可．
【详解】解：如图所示标注字母，根据题意得：
，，，，
∴，
，
∴，
在中，，
∴（海里），
∴此时与灯塔的距离约为海里．
故选：C．

【点睛】本题考查解直角三角形的应用—方向角问题，理解题意，熟练掌握锐角三角函数的定义是解题的关键．也考查了三角形的内角和定理和直角三角形两锐角互余．
10. 观察下列等式：，，，，，，…，根据其中的规律可得的结果的个位数字是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】由已知可得尾数，，，的规律是4个数一循环，则的结果的个位数字与的个位数字相同，即可求解．
【详解】解：∵，，，，，，…，
∴尾数，，，的规律是4个数一循环，
∵，
∴的个位数字是，
又∵，
∴的结果的个位数字与的个位数字相同，
∴的结果的个位数字是．
故选：A．
【点睛】本题考查数的尾数特征，能够通过所给数的特点，确定尾数的循环规律是解题的关键．
二、填空题（每小题3分，共15分）
11. 用一根小木棒与两根长分别为、的小木棒围成三角形，则这根小木棒的长度可以为__________（写出一个即可）
【答案】（答案不唯一）
【解析】
【分析】根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边，即可求第三根木条的取值范围．
【详解】解：设这根木棒长为，
∵这根木棒与两根长分别为、的小木棒围成三角形，
∴，即，
即的取值范围是，在这一范围内任意长度都可以．
故答案为：（答案不唯一）．
【点睛】本题考查三角形三边关系，实际上就是根据三角形三边关系定理列出不等式，然后解不等式，确定取值范围即可．掌握三角形三边关系定理是解题的关键．
12. 若关于x的没有实数根，则k的最小整数值是___________．
【答案】2
【解析】
【分析】根据题意由一元二次方程没有实数根，则根的判别式列不等式，即可得到答案．
【详解】根据题意得：，
解得：，
则的最小整数解为2．
故答案为：2．
【点睛】本题考查了一元二次方程 (为常数)的根的判别式，理解根的判别式对应的根的三种情况是解题的关键．当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程没有实数根．
13. 如图，在中，，观察尺规作图的痕迹，若，则的长是______．

【答案】
【解析】
【分析】由已知条件可得，由作图知于点E，再根据勾股定理求解即可．
【详解】解：∵，
∴，
由作图知于点E，
∴，
∴，
故答案为：．
【点睛】本题主要考查作图—基本作图，解题的关键是掌握过直线外一点作已知直线的垂线的尺规作图及等腰三角形的性质、勾股定理．
14. 等腰直角三角形 中， 为 上一点， ，以 为圆心， 为半径画弧交 于点 ， 交 的延长线于点 ， 则图中阴影部分面积为_______________．

【答案】
【解析】
【分析】连接，利用勾股定理求得，利用在直角三角形中，角所对的直角边等于斜边的一半即可求得，再利用即可求得答案．
【详解】解：连接，

由已知可得，
在中，，，，
，
又，
，
，，
，
故答案为：．
【点睛】本题考查了勾股定理的应用、直角三角形特殊角的性质、扇形面积公式，熟练掌握勾股定理及直角三角形特殊角的性质是解题的关键．
15. 【实践操作】将一张直角三角形纸片沿一条直线剪掉一张三角形纸片，剩下一张如图所示的四边形纸片，其中，，，，，那么剪掉的三角形纸片的面积是___________．

【答案】或
【解析】
【分析】分两种情况讨论，先由三角形面积公式求出四边形的面积，然后根据相似三角形的性质，即可解决问题．
【详解】解：①分别延长，交于，连接，设的面积是，
∵，，，，，
∴四边形的面积为：
，
∴，，
∵，，
∴，
∴，
∴，
解得：，
经检验，是原方程的解且符合题意；

②分别延长，交于，设的面积是，
由（1）知四边形的面积为，
∴，
∵，，，，，
∴，
∵，
∴，
∴，
∴，
解得：，
经检验，是原方程的解且符合题意；
∴剪掉的三角形纸片的面积是或．
故答案为：或．

【点睛】本题考查相似三角形判定和性质．解题的关键是应用相似三角形的性质，分两种情况讨论．
三、解答题（共8个小题，满分75分）
16. 计算：
（1）；
（2）．
【答案】（1）
（2）
【解析】
【分析】（1）先利用特殊角三角函数值、负整数指数幂和二次根式的性质化简，再进行加减运算即可；
（2）先通分化为同分母再进行加减运算，然后进行分式的除法运算，结果化为最简形式．
【小问1详解】
解：

；
【小问2详解】




．
【点睛】本题考查实数运算、特殊角的三角函数值以及分式的化简，正确化简各数以及掌握分式的基本运算法则是解题的关键．
17. 【问题情境】大自然中的植物千姿百态，如果细心观察，就会发现：不同植物的叶子通常有着不同的特征，如果我们用数学的眼光来观察，会有什么发现呢？“数智”小组的四位同学开展了“利用树叶的特征对树木进行分类”的项目化学习活动．

【实践发现】同学们从收集的杨树叶、柳树叶中各随机选取10片，通过测量得到这些树叶的长和宽（单位：cm）的数据后，分别计算长宽比，整理数据如下：
序号
1
2
3
4
5
6
7
8
9
10
杨树叶的长宽比
2
2.4
2.1
2.4
2.8
1.8
2.4
2.2
2.1
1.7
柳树叶的长宽比
1.5
1.6
1.5
1.4
1.5
1.4
1.7
1.5
1.6
1.4
【实践探究】分析数据如下：

平均数
中位数
众数
方差
杨树叶的长宽比
2.19

2.4
0.0949
柳树叶的长宽比
1.51
1.5

0.0089
【问题解决】
（1）上述表格中：______，______；
（2）①这两种树叶从长宽比的方差来看，______树叶的形状差别较小；
②该小组收集树叶中有一片长为11.5cm，宽为5cm的树叶，这片树叶来自于______树的可能性大；
（3）该小组准备从四位成员中随机选取两名同学进行成果汇报，请用列表或画树状图的方法求成员小颖和小娜同时被选中的概率．
【答案】（1）2.15，1.5
（2）①柳；②杨 （3）
【解析】
【分析】（1）根据中位数和众数的定义解答即可；
（2）①根据题目给出的方差判定即可；②根据树叶的长宽比判定即可；
（3）列表得出所有等可能结果，从中找到符合条件的结果数，再根据概率公式求解即可．
【小问1详解】
解：将杨树叶的长宽比按从小到大的顺序排序为：
1.7，1.8，2，2.1，2.1，2.2，2.4，2.4，2.4，2.8，
则其中位数是第5和第6的平均数，即：；
柳树叶的长宽比的众数为1.5；
故答案为：2.15，1.5；
【小问2详解】
①∵杨树叶的长宽比的方差为0.0949大于柳树叶的长宽比的方差0.0089，
∴柳树叶的形状差别较小；
故答案为：柳；
②∵该小组收集的树叶中有一片长为11.5cm，宽为5cm的树叶，
则长宽比为2.3，
∴这片树叶来自于杨树的可能性大；
故答案为：杨；
【小问3详解】
四名同学用A，B，C，D表示，其中A表示小颖，B表示小娜，根据题意，列表如下：

A
B
C
D
A




B




C




D




由列表（或树状图）可知共有12种可能出现的结果，且每种结果出现的可能性都相同，其中小颖和小娜同时被选中的结果共有2种．
∴（小颖和小娜同时被选中）．
【点睛】本题考查了众数，中位数，平均数和方差，掌握相关定义是关键．还考查了用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件．用到的知识点为：概率所求情况数与总情况数之比．
18. 【阅读与思考】平移是初中几何变换之一，它可以将线段和角平移到一个新的位置，从而把分散的条件集中到一起，使问题得以解决．
【问题情景】如图1，在正方形中中，E、F、G分别是、、上的点，于点O，求证：．
小明尝试平移线段到，构造≌，使问题得到解决．

（1）【阅读理解】按照小明的思路，证明≌的依据是_______；
（2）【尝试应用】
如图2，在5×6的正方形网格中，点A、B、C、D为格点，交于点M．则的度数为_________；
（3）如图3，在正方形方格纸中，每个小正方形的边长都相等，A、B、C、D都在格点处，与相交于点P，求的值．
【答案】（1）
（2）
（3）
【解析】
【分析】对于（1），根据正方形的性质得出两组角及夹边对应相等，即可得出答案；
对于（2），平移至，根据勾股定理可得是直角三角形，进而求出，根据平行线的性质得出答案；
对于（3），平移至，根据勾股定理可知是直角三角形，即可得出，再根据平行线的性质得出答案．
【小问1详解】
∵四边形是正方形，

∴，，
∴．
∵，且，
∴，
∴，
∴．
∵，，
∴≌．
故答案为：；
【小问2详解】
将平移至，
设正方形的边长为1，根据勾股定理可知，，，
∴，且，
∴是直角三角形，且，
∴．
∵，
∴．
故答案为：；
【小问3详解】
将平移至，
设正方形的边长为1，根据勾股定理，得，，，
∴，，，
∴是直角三角形，且，
则．
∵，
∴，
∴．

【点睛】本题主要考查了正方形的性质，平移的应用，全等三角形的性质和判定，勾股定理及其逆定理，锐角三角函数值等，根据平移构造直角三角形是解题的关键．
19. 环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mgL．环保局要求该企业立即整改，在15天以内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AB表示前3天的变化规律，其中第3天时硫化物的浓度降为4mgL．从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系：
时间x（天）
3
4
5
6
8
……
硫化物的浓y（mg/L）
4
3
2.4
2
1.5



（1）求整改过程中当0≤x＜3时，硫化物的浓度y与时间x的函数表达式；
（2）求整改过程中当x≥3时，硫化物的浓度y与时间x的函数表达式；
（3）该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0mgL？为什么？
【答案】(1) y=﹣2x+10；(2) y=；（3）该企业所排污水中硫化物的浓度，能在15天以内不超过最高允许的1.0mg/L，理由详见解析．
【解析】
【分析】（1）设线段AB的函数表达式为：y=kx+b，把A、B两点坐标代入求出k、b的值即可.（2）设函数的表达式为：y=，把B点坐标代入，求出k的值即可.（3）根据（2）所得表达式，求出x=15时，y的值与硫化物浓度允许的最高值比较即可.
【详解】（1）前三天的函数图象是线段，设函数表达式为：y=kx+b
把（0，10）（3，4）代入函数关系式，得
解得：k=﹣2，b=10
所以当0≤x＜3时，硫化物的浓度y与时间x的函数表达式为：y=﹣2x+10；
（2）当x≥3时，设y=
把（3，4）代入函数表达式，得4=
所以k=12
当x≥3时，硫化物的浓度y与时间x的函数表达式为：y=
（3）能．理由：
当x=15时，y==0.8
因为0.8＜1，
所以该企业所排污水中硫化物的浓度，能在15天以内不超过最高允许的1.0mgL
【点睛】本题考查一次函数和反比例函数，熟练掌握根据坐标确定解析式的一次项系数和常数项是解题关键.
20. 如图，是的直径，是的弦，过点作的切线，交的延长线于点，过点作于点，交的延长线于点．

（1）求证：；
（2）若，的半径是，求的长．
【答案】（1）证明见解析
（2）
【解析】
【分析】（1）连接，由切线的性质可得，从而可推出，根据平行线的性质得出，根据等腰三角形的性质得出，再根据三角形的外角的性质可得，从而得证；
（2）根据，可得，由等角对等边可得，然后在中利用解直角三角形计算出，从而可得，最后在中利用解直角三角形计算出，最后利用可得出答案．
【小问1详解】
证明：连接，
∵是的切线，
∴，
∵，
∴，
∴，
∵，
∴，
∴，
∴；
【小问2详解】
解：∵，，
∴，
∵是的直径，的半径是，，
∴，
在中，
∵，
∴，
∴，
在中，
∵，
∴，
∴．
∴的长为．
【点睛】本题考查切线的性质，解直角三角形的应用，等腰三角形的判定和性质，平行线的判定和性质，三角形外角的性质等知识点．掌握切线的性质及三角函数的定义是解题的关键．
21. 2023春节档电影《满江红》热映，进一步激发观众爱国之情．帝都南阳与名将岳飞有着一段传颂至今的历史——公元1138年，岳飞统军过南阳到武侯祠敬拜诸葛亮，雨夜含泪手书前后《出师表》，为南阳留下了千古绝唱“三绝碑”．
某超市采购了两批同样的《出师表》纪念品挂件，第一批花了3300元，第二批花了4000元，已知第一批每个挂件的进价是第二批的倍，且第二批比第一批多购进25个．

（1）求第二批每个挂件的进价；
（2）两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？
【答案】（1）40元 （2）售价定为55元时，最大利润是1350元
【解析】
【分析】（1）设第二批每个挂件的进价为x元，则第一批每个挂件的进价为元，根据题意列出方程，求解即可；
（2）设每个售价定为m元，每周所获利润为W元，则可列出W关于m的函数关系式，再根据“每周最多能卖90个”得出m的取值范围，根据二次函数的性质可得出结论．
【小问1详解】
解答：解：(1）设第二批每个挂件进价是每个x元，
根据题意得
解得，
经检验，是原方程的解，也符合题意，
∴，
答：第二批每个挂件进价是每个40元；
【小问2详解】
设每个挂件售价定为m元，每周可获得利润W元，
∵每周最多能卖90个，
∴ ，
解得，
根据题意得，
∵，
∴当时，y随x的增大而减小，
∵，
∴当时，W取最大，此时．
∴当每个挂件售价定为55元时，每周可获得最大利润，最大利润1350元．
【点睛】本题综合考查分式方程和二次函数的应用，根据题意列出函数关系式是解题关键．
22. 综合与实践课上，诸葛小组三位同学对含角的菱形进行了探究．
【背景】在菱形中，，作，、分别交边、于点、．

（1）【感知】如图1，若点是边的中点，小南经过探索发现了线段与之间的数量关系，请你写出这个关系式___________．
（2）【探究】如图2，小阳说“点为上任意一点时，（1）中的结论仍然成立”，你同意吗？请说明理由．
（3）【应用】小宛取出如图3所示的菱形纸片，测得，，在边上取一点，连接，在菱形内部作，交于点，当时，请直接写出线段的长．
【答案】（1）
（2）同意，理由见解析
（3）或
【解析】
【分析】（1）数量关系：．连接，利用菱形的性质和等边三角形的三线合一性质证明即可；
（2）利用菱形的性质和等边三角形的性质证明即可；
（3）利用菱形的性质和等边三角形的性质可得，利用勾股定理求出，，分当点在点的左侧和点在点的右侧两种情况，可得或，再利用（2）中的结论即可得出结论．
【小问1详解】
线段与之间的数量关系：．
理由：如图，连接，
∵四边形是菱形，且，
∴，，
∴和都是等边三角形，
∴，，
∵点是边的中点，
∴，，
∵，
∴，
∴，
∴，
∴，
∴，
在和中，
，
∴
∴，
故答案为：．
【小问2详解】
同意．
理由：如图，连接，
∵四边形是菱形，且，
∴，，
∴和都是等边三角形，
∴，，，
∴，
∵，
∴，
∴，
在和中，
，
∴，
∴．
【小问3详解】
解：如图，过点作于，连接，
∵四边形是菱形，且，，
∴，
∴是等边三角形，
∴，
∴，
∵，
∴，
当点在点的左侧时，，
当点在点的右侧（图中处）时，，
∴或，
由（2）知：，
∴，
∴或．
∴线段的长为或．

【点睛】本题是四边形综合题，考查了菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理等知识，运用了分类讨论的思想．解题的关键是添加适当的辅助线构造全等三角形．
23. 如图，三孔桥横截面的三个孔都呈抛物线形，左右两个抛物线形是全等的，正常水位时，大孔水面宽度为，顶点距水面（即），小孔顶点距水面（即，建立如图所示的平面直角坐标系．

（1）求出大孔抛物线的解析式；
（2）航管部门设定警戒水位为正常水位上方处，汛期某天水位正好达到警戒水位，有一艘顶部高出水面，顶部宽的巡逻船要路过三孔桥，请问该巡逻船能否安全通过大孔？并说明理由．
（3）当水位上涨到刚好淹没小孔时，求出大孔的水面宽度．
【答案】（1）
（2）能安全通过大孔，理由见解析
（3）
【解析】
【分析】（1）用待定系数法即可得大孔抛物线的解析式；
（2）求出时的值，与作比较即可；
（3）求出点、坐标，即可得到答案．
【小问1详解】
解：设大孔抛物线的解析式为，
把点代入解析式得：，
解得：，
∴大孔抛物线的解析式为．
【小问2详解】
∵大孔抛物线的解析式为，
当时，，
∴该巡逻船能安全通过大孔；
【小问3详解】
∵，
∴点的纵坐标为，
∴当时，得，
解得：，，
∴由抛物线对称性可知点为，点为，
∴．
答：大孔的水面宽度为．
【点睛】本题考查二次函数的应用，解题关键是建立函数模型，准确找出模型类型，然后利用待定系数法求出模型（即函数）的表达式，最后根据函数的性质得出结论．掌握二次函数的性质是解题的关键．