





初中冀教版3.3 代数式的值教案配套课件ppt
展开求代数式的值整体代入求代数式的值程序计算求代数式的值实际应用求代数式的值
据报纸记载,一位医生研究得出父母身高可以预测子女成年后的身高公式:儿子身高是由父母身高的和的一半,再乘以1.08,女儿的身高是父亲身高的0.923倍,再加上母亲身高的和再除以2.读完上边的内容,你能完成下边的问题吗?(1)已知父亲身高是a米,母亲身高是b米,成年后儿 子和女儿的身高应该怎样利用代数式表示呢?
(2)七年级一班女生小红的父亲身高是1.75米,母亲 身高是1.62 米,七年级二班男生小明的父亲身高 是1.70米,母亲身高是1.62米,你能预测成年后, 小红与小明谁个子更高吗?(3)想知道你成年后的身高吗?
1. 当n取4,10,13,25等值时,分别代入上面的代数式,计算出代数式4n-4相应的值. 对于n的同一个值,同学们得到的结果都相同吗?2. 以n=4和n=13为例,说明你是如何算出4n-4的值的.
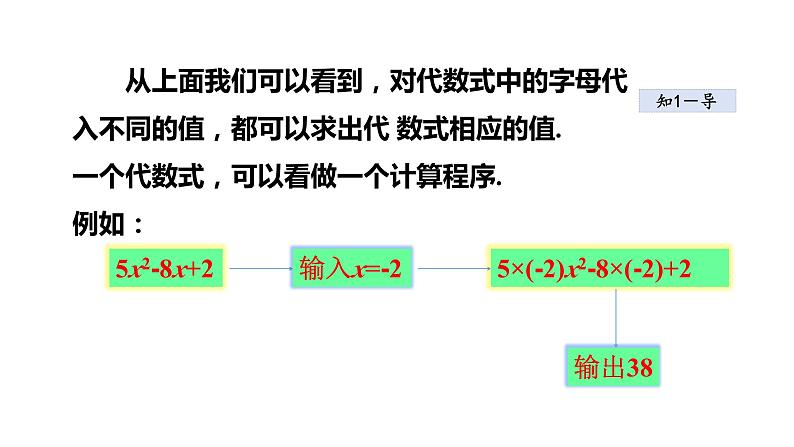
从上面我们可以看到,对代数式中的字母代入不同的值,都可以求出代 数式相应的值.一个代数式,可以看做一个计算程序.例如:
5×(-2)x2-8×(-2)+2
1. 按上面的程序,计算x=3,x=6时的输出值.2. 任意取x的两个值,请同桌的同学完成上面的求 值过程,并相互检查求值过程和结果是否正确.
定义:一般地,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫做代数式的值.这个过程叫做求代数式的值.
特别提醒1. 代入数值时不要代错,特别是代数式里有多个字母时,要注意“对号入座”;2. 代数式不是最简形式时,可先化简代数式,再代入数值求值;3. 代数式里原来省略的乘号,代入数值时必须添上.
当x=-1,y=3 时,求下列代数式的值: (1) x3-2y;(2) (3) .
用直接代入法求代数式的值可以分三步:①“当……时”,即指出字母的值;②“原式=……”,即代入所给字母的值;③ 计算.
2.【中考·重庆】若a=2,b=-1,则a+2b+3的值为( )A.-1 B.3 C.6 D.53.【中考·菏泽】当1<a<2时,代数式|a-2|+|1-a|的值是( )A.-1 B.1 C.3 D.-3
用整体代入法求代数式的值的方法:给出一个含字母的代数式的值,当单个字母的值不能或不容易求出时,一般对给出的代数式或要求值的代数式进行适当变形,通过整体代入,实现快速求值.
1.已知代数式14x+5-21x2的值是-2,求6x2-4x+5的值.
解:因为14x+5-21x2的值是-2,所以14x-21x2=-7,即2x-3x2=-1.所以3x2-2x=1.所以6x2-4x+5=2×(3x2-2x)+5=7.
2.当代数式x2+3x+5的值为7时,求代数式3x2+9x-2的值.
3.【中考·淮安】已知a-b=2,则代数式2a-2b-3的值是( )A.1 B.2 C.5 D.7
解:由代数式x2+3x+5的值为7得x2+3x=2,所以3x2+9x-2=3(x2+3x)-2=4.
[图形信息题]按图所示的程序计算.(1)若开始输入的n的值为20,则最 后输出的结果y为多少?(2)若开始输入的n的值为4,则最 后输出的结果y为多少?
解:(1)当n=20时, =190>100, 所以最后输出的结果y为190.(2)当n=4时, =6<100, 当n=6时, =15<100, 当n=15时, =105>100, 所以最后输出的结果y为105.
解答本题的关键是弄清楚给出的计算程序,利用转化思想求解.
1.[图形信息题,规律探究题]如图所示的运算程序中,若开始输入的x的值为48,请回答下列问题:(1)第1次输出的结果为_____, 第2次输出的结果为_____;(2)第2 015次输出的结果为____.
2.【中考·安顺】根据如图所示的程序计算,若输入x的值为1,则输出y的值为________.
已知某林场现有的木材蓄积量为a m3,预计今后两年的木材蓄积量的年平均增长率为p%,那么两年后该林场的木材蓄积量将达到多少立方米?若a=2 000,p=10,则两年后该林场的木材蓄积量将达到多少立方米?
导引:现有的木材蓄积量为a m3,木材蓄积量的年平均增长率为p%,所以一年后该林场的木材蓄积量为a(1+p%) m3,两年后该林场的木材蓄积量为a(1+p%)(1+p%)m3.
解:由题意得,一年后该林场的木材蓄积量为a(1+p%)m3,两年后该林场的木材蓄积量为a(1+p%)(1+p%)m3.当a=2 000,p=10时,a(1+p%)(1+p%)=2 000×(1+10%)×(1+10%)=2 420 .故两年后该林场的木材蓄积量将达到a(1+p%)(1+p%)m3.若a=2 000,p=10,则两年后该林场的木材蓄积量将达到2 420 m3.
本题运用了转化思想.把实际要解决的问题转化为求代数式的值的问题.
1.某种摩托车的行车里程与耗油量有如下关系:(1)用x表示耗油量,用y表示行车里程,请用含x的代数式表示y;(2)行车里程为210 km时,耗油量是多少?(3)如果耗油量为2.7 L,可行多少千米?
解:(1)y=60x.(2)当y=210时,210=60x,x=3.5.即行车里程为210 km时,耗油量是3.5 L.(3)当x=2.7时,y=60×2.7=162.即耗油量为2.7 L时,可行162 km.
2.【中考·天水】有一根40 cm的金属棒,欲将其截成x根7 cm的小段和y根9 cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为( )A.x=1,y=3 B.x=4,y=1C.x=3,y=2 D.x=2,y=3
数学第三章 代数式3.3 代数式的值备课课件ppt: 这是一份数学第三章 代数式3.3 代数式的值备课课件ppt,共20页。PPT课件主要包含了x+5,x–5,北京时间,莫斯科时间,x+1,东京时间,请你来批改,b²–4ac,2–1²,+1–4等内容,欢迎下载使用。
2021学年3.3 代数式的值图片课件ppt: 这是一份2021学年3.3 代数式的值图片课件ppt,共17页。PPT课件主要包含了知识点,求代数式的值,知1-讲,整体代入求代数式的值等内容,欢迎下载使用。
初中数学冀教版七年级上册3.3 代数式的值图片课件ppt: 这是一份初中数学冀教版七年级上册3.3 代数式的值图片课件ppt,共22页。PPT课件主要包含了a+b2,a2+b2,n的两倍与10的和,%ɑ+b,导入新课,游戏规则,x+1,用代数式表示为,新知探究,代数式的值等内容,欢迎下载使用。













