2023年安徽省马鞍山市雨山区花园初级中学中考数学一模试卷

这是一份2023年安徽省马鞍山市雨山区花园初级中学中考数学一模试卷，共22页。试卷主要包含了单项选择题，填空题等内容，欢迎下载使用。
2023年安徽省马鞍山市雨山区花园初级中学中考数学一模试卷
一、单项选择题（本大题共10个小题，每小题4分，共40分）
1．（4分）记4的算术平方根为a，则a的相反数是（　　）
A．﹣4 B．﹣2 C．±2 D．±4
2．（4分）下列运算正确的是（　　）
A．（m4）3＝m7 B．m4﹣m3＝m C．m4⋅m3＝m7 D．m4⋅m3＝m12
3．（4分）截至2022年4月21日，全国已接种新冠病毒疫苗332248.8万剂次．332248.8万用科学记数法可表示为（　　）
A．33.22488×104 B．0.3322488×105
C．3.322488×109 D．3.322488×105
4．（4分）某个几何体的三视图如图所示，该几何体是（　　）

A． B．
C． D．
5．（4分）某中学开展“读书伴我成长”活动，为了解八年级学生四月份的读书册数，对从中随机抽取的20名学生的读书册数进行调查
册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
根据统计表中的数据，这20名同学读书册数的众数，中位数分别是（　　）
A．3，3 B．3，7 C．2，7 D．7，3
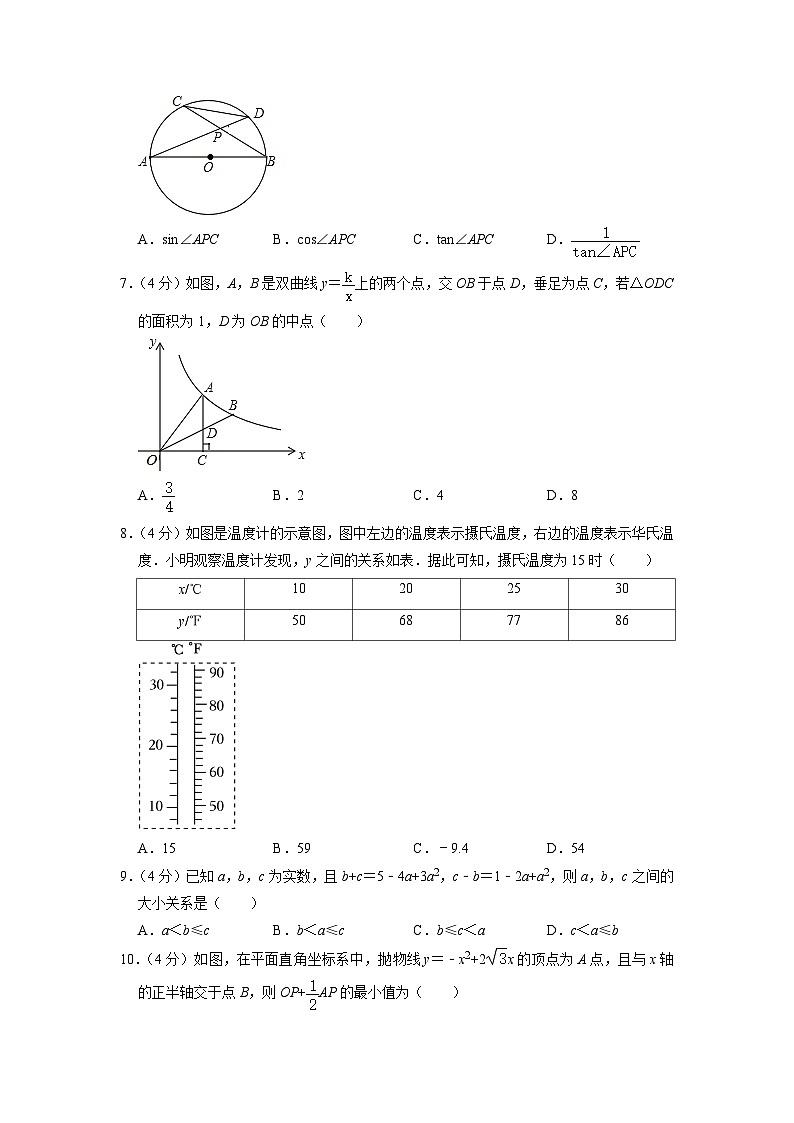
6．（4分）已知：如图，AB是⊙O的直径，弦AD、BC相交于P点的值为（　　）

A．sin∠APC B．cos∠APC C．tan∠APC D．
7．（4分）如图，A，B是双曲线y＝上的两个点，交OB于点D，垂足为点C，若△ODC的面积为1，D为OB的中点（　　）

A． B．2 C．4 D．8
8．（4分）如图是温度计的示意图，图中左边的温度表示摄氏温度，右边的温度表示华氏温度．小明观察温度计发现，y之间的关系如表．据此可知，摄氏温度为15时（　　）
x/℃
10
20
25
30
y/℉
50
68
77
86

A．15 B．59 C．﹣9.4 D．54
9．（4分）已知a，b，c为实数，且b+c＝5﹣4a+3a2，c﹣b＝1﹣2a+a2，则a，b，c之间的大小关系是（　　）
A．a＜b≤c B．b＜a≤c C．b≤c＜a D．c＜a≤b
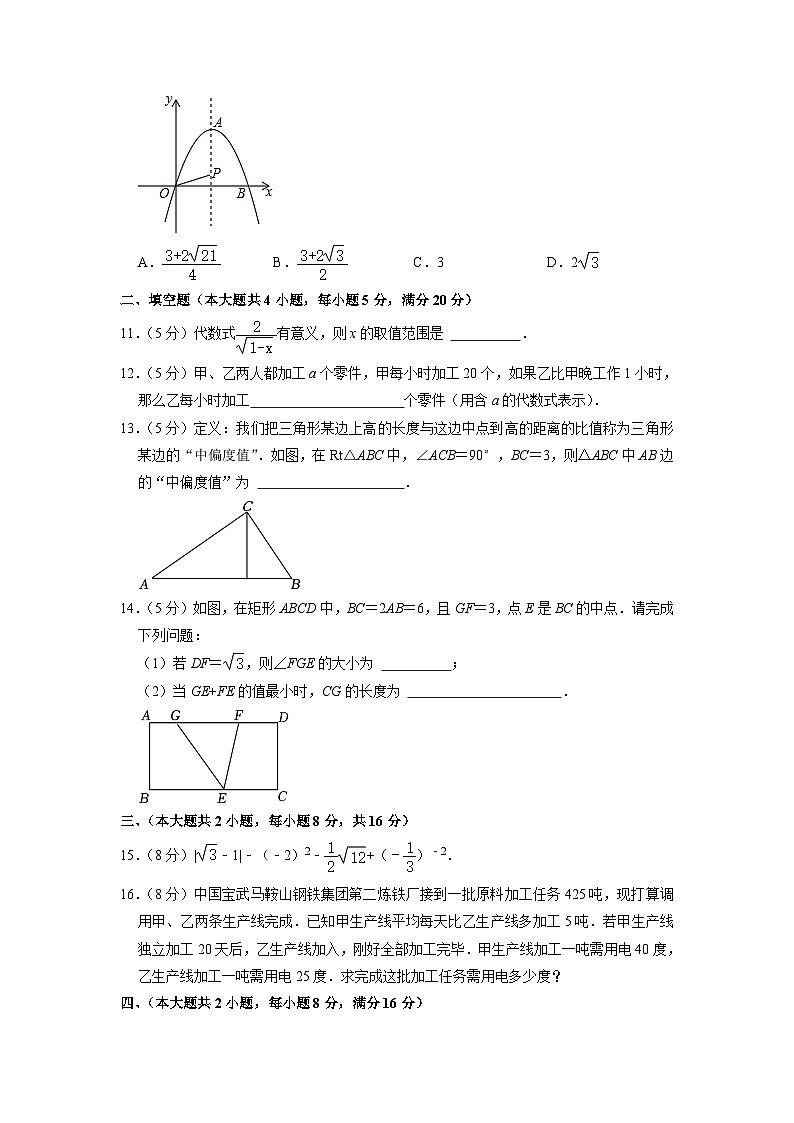
10．（4分）如图，在平面直角坐标系中，抛物线y＝﹣x2+2x的顶点为A点，且与x轴的正半轴交于点B，则OP+AP的最小值为（　　）

A． B． C．3 D．2
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）代数式有意义，则x的取值范围是 　 　．
12．（5分）甲、乙两人都加工a个零件，甲每小时加工20个，如果乙比甲晚工作1小时，那么乙每小时加工　 　个零件（用含a的代数式表示）．
13．（5分）定义：我们把三角形某边上高的长度与这边中点到高的距离的比值称为三角形某边的“中偏度值”．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，则△ABC中AB边的“中偏度值”为 　 　．

14．（5分）如图，在矩形ABCD中，BC＝2AB＝6，且GF＝3，点E是BC的中点．请完成下列问题：
（1）若DF＝，则∠FGE的大小为 　 　；
（2）当GE+FE的值最小时，CG的长度为 　 　．

三、（本大题共2小题，每小题8分，共16分）
15．（8分）|﹣1|﹣（﹣2）2﹣+（﹣）﹣2．
16．（8分）中国宝武马鞍山钢铁集团第二炼铁厂接到一批原料加工任务425吨，现打算调用甲、乙两条生产线完成．已知甲生产线平均每天比乙生产线多加工5吨．若甲生产线独立加工20天后，乙生产线加入，刚好全部加工完毕．甲生产线加工一吨需用电40度，乙生产线加工一吨需用电25度．求完成这批加工任务需用电多少度？
四、（本大题共2小题，每小题8分，满分16分）
17．（8分）观察以下等式：
第1个等式：﹣+＝1，
第2个等式：﹣+＝1，
第3个等式：+＝1，
第4个等式：﹣+＝1，
……
按照以上规律，解决下列问题：
（1）写出第5个等式：；
（2）写出你猜想的第n（n为正整数）个等式：（用含n的等式表示），并证明．
18．（8分）如图，在12×12的正方形网格中，每个小正方形的边长都是1，B，C，D均为网格线的交点．
（1）在网格中将△ABC绕点D顺时针旋转90°，画出旋转后得到的△A1B1C1（点A，B，C的对应点分别为点A1，B1，C1）；
（2）在网格中画出△DEF，使△DEF∽△ABC，且相似比为2：1（点E，F为格点）；
（3）若M是线段AB上的一个动点（可以与两端点重合），△A1DM的面积为S，则S的取值范围是 　 　．

五、（本大题共2小题，每小题10分，满分20分）
19．（10分）如图，点B为圆O外一点，过点B作圆O的切线，点P为OB上一点，连接AP并延长交圆O于点C，若OB与OC垂直．
（1）求证：BP＝AB；
（2）若OB＝10，圆O的半径为8，求AP的长．

20．（10分）桑梯是我国古代发明的一种采桑工具．图1是明朝科学家徐光启在《农政全书》中用图画描绘了桑梯，已知如图2所示，AB＝AC，AD＝1.2米，∠CAB＝40°
（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

六、（本题满分12分）
21．（12分）国际数学奥林匹克竞赛（IMO）是匈牙利数学界为纪念数理学家厄特沃什•罗兰于1894年组织的数学竞赛，是目前最高等次的国际数学竞赛．下面是甲、乙两校参赛队员在某次预选赛中成绩情况（试卷总分为42分）：
甲校：28，30，22，39，23，35，37，35，35，34，38
乙校：36，33，39，33，32，34，23，28，29，30，30
（1）整理数据：
组别
A．18≤x＜24
B.24≤x＜30
C.30≤x＜36
D.36≤x＜42
甲校
2
a
6
b
乙校
1
c
8
2
填空：a＝　 　，b＝　 　，c＝　 　；
（2）甲校15名学生成绩的中位数落在　 　组内；（填“A”“B”“C”或“D”）
（3）经统计，本次预选赛分数在D组的进入下一轮，现从进入下一轮同学中任选两人成绩进行分析
七、（本题满分12分）
22．（12分）已知：如图，在菱形ABCD中，AE⊥BC，垂足分别为点E和点F，AE、AF分别与BD相交于点M、N．
（1）求证：EF∥BD；
（2）当MN：EF＝2：3时，求证：△AMN是等边三角形．

八、（本题满分14分）
23．（14分）已知直线y＝kx+1经过点（2，3），与抛物线y＝x2+bx+c的对称轴交于点（n，）．
（1）求k，b的值；
（2）抛物线y＝x2+bx+c与x轴交于（x1，0）（x2，0），且3≤x2﹣x1＜9，若p＝x12﹣3x22，求P的最大值；
（3）当﹣1＜x＜2时，抛物线y＝x2+bx+c与直线y＝kx+1有且只有一个公共点，直接写出c的取值范围．

2023年安徽省马鞍山市雨山区花园初级中学中考数学一模试卷
（参考答案）
一、单项选择题（本大题共10个小题，每小题4分，共40分）
1．（4分）记4的算术平方根为a，则a的相反数是（　　）
A．﹣4 B．﹣2 C．±2 D．±4
【解答】解：∵4的算术平方根为a，
∴a＝2，
则a的相反数是：﹣4．
故选：B．
2．（4分）下列运算正确的是（　　）
A．（m4）3＝m7 B．m4﹣m3＝m C．m4⋅m3＝m7 D．m4⋅m3＝m12
【解答】解：A、（m4）3＝m12，故A不符合题意；
B、m7与﹣m3不属于同类项，不能合并；
C、m4⋅m6＝m7，故C符合题意；
D、m4⋅m2＝m7，故D不符合题意；
故选：C．
3．（4分）截至2022年4月21日，全国已接种新冠病毒疫苗332248.8万剂次．332248.8万用科学记数法可表示为（　　）
A．33.22488×104 B．0.3322488×105
C．3.322488×109 D．3.322488×105
【解答】解：332248.8万＝3322488000＝3.322488×102．
故选：C．
4．（4分）某个几何体的三视图如图所示，该几何体是（　　）

A． B．
C． D．
【解答】解：由三视图可知这个几何体是：

故选：A．
5．（4分）某中学开展“读书伴我成长”活动，为了解八年级学生四月份的读书册数，对从中随机抽取的20名学生的读书册数进行调查
册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
根据统计表中的数据，这20名同学读书册数的众数，中位数分别是（　　）
A．3，3 B．3，7 C．2，7 D．7，3
【解答】解：这20名同学读书册数的众数为3册，中位数为，
故选：A．
6．（4分）已知：如图，AB是⊙O的直径，弦AD、BC相交于P点的值为（　　）

A．sin∠APC B．cos∠APC C．tan∠APC D．
【解答】解：连接AC．

∵∠D＝∠B，∠CPD＝∠APB，
∴△CPD∽△APB．
∴．
∵AB是⊙O的直径，
∴∠ACB＝90°．
∴＝cos∠APC．
∴．
故选：B．
7．（4分）如图，A，B是双曲线y＝上的两个点，交OB于点D，垂足为点C，若△ODC的面积为1，D为OB的中点（　　）

A． B．2 C．4 D．8
【解答】解：过点B作BE⊥x轴于点E，则S△BOE＝k．
∵D为OB的中点，CD∥BE，
∴CD是△OBE的中位线，CD＝，
∴△ODC∽△OBE，
∴＝（）2＝，
∴S△ODC＝S△BOE＝k＝4，
∴k＝8．
故选：D．

8．（4分）如图是温度计的示意图，图中左边的温度表示摄氏温度，右边的温度表示华氏温度．小明观察温度计发现，y之间的关系如表．据此可知，摄氏温度为15时（　　）
x/℃
10
20
25
30
y/℉
50
68
77
86

A．15 B．59 C．﹣9.4 D．54
【解答】解：设该一次函数的表达式为y＝kx+b（k≠0），
∵经过点（10，50）和（20，
∴，
解得，
∴y＝1.8x+32，
当x＝15时，y＝4.8×15+32＝27+32＝59，
即摄氏温度为15时，对应的华氏温度应为59．
故选：B．
9．（4分）已知a，b，c为实数，且b+c＝5﹣4a+3a2，c﹣b＝1﹣2a+a2，则a，b，c之间的大小关系是（　　）
A．a＜b≤c B．b＜a≤c C．b≤c＜a D．c＜a≤b
【解答】解：∵b+c＝5﹣4a+3a2①，c﹣b＝1﹣6a+a2②，
∴①+②得2c＝4a2﹣6a+5，即c＝2a2﹣4a+3，
∴①﹣②得2b＝6a2﹣2a+8，即b＝a2﹣a+2．
∵b﹣a＝a3﹣a+2﹣a＝（a﹣1）8+1＞0，
∴b＞a．
又∵c﹣b＝7a2﹣3a+2﹣（a2﹣a+2）＝a5﹣2a+1＝（a﹣5）2≥0，
∴c≥b，
∴a＜b≤c．
故选：A．
10．（4分）如图，在平面直角坐标系中，抛物线y＝﹣x2+2x的顶点为A点，且与x轴的正半轴交于点B，则OP+AP的最小值为（　　）

A． B． C．3 D．2
【解答】解：连接AO、AB，作PH⊥OA于H，如图，
当y＝0时，﹣x2+5x＝08＝0，x2＝2，则B（2，
y＝﹣x2+2x＝﹣（x﹣）2+6，则A（，
∴OA＝＝7，
而AB＝AO＝2，
∴AB＝AO＝OB，
∴△AOB为等边三角形，
∴∠OAP＝30°，
∴PH＝AP，
∵AP垂直平分OB，
∴PO＝PB，
∴OP+AP＝PB+PH，
当H、P、B共线时，最小值为BC的长，
而BC＝AB＝＝3，
∴OP+AP的最小值为3．
故选：C．

二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）代数式有意义，则x的取值范围是 　x＜1　．
【解答】解：由题意得：1﹣x＞0，
解得：x＜5，
故答案为：x＜1．
12．（5分）甲、乙两人都加工a个零件，甲每小时加工20个，如果乙比甲晚工作1小时，那么乙每小时加工　　个零件（用含a的代数式表示）．
【解答】解：甲加工a个零件需要是时间是，乙工作时间是．
则乙每小时加工的零件是：＝．
故答案是：．
13．（5分）定义：我们把三角形某边上高的长度与这边中点到高的距离的比值称为三角形某边的“中偏度值”．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，则△ABC中AB边的“中偏度值”为 　　．

【解答】解：作CD⊥AB于点D，CE为△ACB的中线，
∵∠ACB＝90°，AC＝4，
∴AB＝＝＝5，
∵＝，
∴，
解得CD＝，
∴BD＝＝＝，
∵CE为Rt△ACB斜边AB上的中线，AB＝5，
∴BE＝，
∴ED＝BE﹣BD＝﹣＝，
即点E到CD的距离为，
∴△ABC中AB边的“中偏度值”为：＝，
故答案为：．

14．（5分）如图，在矩形ABCD中，BC＝2AB＝6，且GF＝3，点E是BC的中点．请完成下列问题：
（1）若DF＝，则∠FGE的大小为 　60°　；
（2）当GE+FE的值最小时，CG的长度为 　　．

【解答】解：（1）过点G作CH⊥BC于点H，由题意知，DF＝BC＝3，

∴AG＝BH＝3﹣，
∴HE＝3﹣（3﹣）＝，
在Rt△GHE中，GH＝，
∴，
∴tan，
即∠HEG＝60°，
∴∠HGE＝30°，
∵∠HGD＝90°，
∴∠FGE＝60°，
故答案为：60°；
（2）过BC作点G的对称点G′，过BC作点F的对称点H，此时，则E为FG′的中点，则M是GF的中点，

∴，
在Rt△CGD中，CG＝，
∵GD＝GM+MD＝，
∴CG＝＝＝，
故答案为：．
三、（本大题共2小题，每小题8分，共16分）
15．（8分）|﹣1|﹣（﹣2）2﹣+（﹣）﹣2．
【解答】解：原式＝﹣1﹣6﹣+9
＝﹣5﹣4﹣
＝8．
16．（8分）中国宝武马鞍山钢铁集团第二炼铁厂接到一批原料加工任务425吨，现打算调用甲、乙两条生产线完成．已知甲生产线平均每天比乙生产线多加工5吨．若甲生产线独立加工20天后，乙生产线加入，刚好全部加工完毕．甲生产线加工一吨需用电40度，乙生产线加工一吨需用电25度．求完成这批加工任务需用电多少度？
【解答】解：设甲生产线每天生产x吨，则乙生产线每天生产（x﹣5）吨，
由题意得20x+5（x+x﹣8）＝425，
解得x＝15，所以x﹣5＝10，
甲生产线每天生产15吨，乙生产线每天生产10吨，
需用电：（20+5）×15×40+5×10×25＝16250（度），
答：完成这批加工任务需用电16250度．
四、（本大题共2小题，每小题8分，满分16分）
17．（8分）观察以下等式：
第1个等式：﹣+＝1，
第2个等式：﹣+＝1，
第3个等式：+＝1，
第4个等式：﹣+＝1，
……
按照以上规律，解决下列问题：
（1）写出第5个等式：；
（2）写出你猜想的第n（n为正整数）个等式：（用含n的等式表示），并证明．
【解答】解：（1）第5个等式为：；
（2）第n个等式为：；

∴等式成立；
18．（8分）如图，在12×12的正方形网格中，每个小正方形的边长都是1，B，C，D均为网格线的交点．
（1）在网格中将△ABC绕点D顺时针旋转90°，画出旋转后得到的△A1B1C1（点A，B，C的对应点分别为点A1，B1，C1）；
（2）在网格中画出△DEF，使△DEF∽△ABC，且相似比为2：1（点E，F为格点）；
（3）若M是线段AB上的一个动点（可以与两端点重合），△A1DM的面积为S，则S的取值范围是 　4≤S≤8　．

【解答】解：（1）如图，△A1B1C4即为所求；
（2）如图，△DEF即为所求；

（3）若M是线段AB上的一个动点（可以与两端点重合），△A1DM的面积为S，
∵S的最大值＝×4×4＝5×6×2＝4，
故答案为：8≤S≤8．
五、（本大题共2小题，每小题10分，满分20分）
19．（10分）如图，点B为圆O外一点，过点B作圆O的切线，点P为OB上一点，连接AP并延长交圆O于点C，若OB与OC垂直．
（1）求证：BP＝AB；
（2）若OB＝10，圆O的半径为8，求AP的长．

【解答】（1）证明：∵OB⊥OC，
∴∠POC＝90°，
∴∠C+∠CPO＝90°，
∵OC＝OA，
∴∠C＝∠OAC，
∴∠OAC+∠CPO＝90°，
∵∠BPA＝∠CPO，
∴∠OAC+∠BPA＝90°，
∵BA与圆切于A，
∴半径OA⊥AB，
∴∠OAC+∠BAP＝90°，
∴∠BAP＝∠BPA，
∴AB＝PB；
（2）解：作BH⊥AP于H，
∵AB＝PB，
∴AP＝2PH，
∵OB＝10，圆O的半径为8，
∴AB＝＝＝6，
∴BP＝AB＝2，
∴OP＝OB﹣PB＝10﹣6＝4，
∴PC＝＝＝4，
∵∠BHP＝∠COP，∠BPH＝∠CPO，
∴△BPH∽△CPO，
∴PH：PO＝BP：CP，
∴PH：4＝2：4，
∴PH＝，
∴AP＝5PH＝，
∴AP的长是．

20．（10分）桑梯是我国古代发明的一种采桑工具．图1是明朝科学家徐光启在《农政全书》中用图画描绘了桑梯，已知如图2所示，AB＝AC，AD＝1.2米，∠CAB＝40°
（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

【解答】解：过A作AE⊥BC于E，
∵AB＝AC，
∴∠ABC＝∠C，
∵∠DAB＝∠ABC+∠C＝140°，
∴∠ABC＝∠C＝70°，
∵AE⊥BC，
∴CE＝BC＝，
在Rt△AEC中，cos∠C＝cos70°＝＝，
∴AC＝≈1.47（米），
∵AD＝1.4米，
∴CD＝2.67（米），
过D作DF⊥BC于F，
在Rt△CDF中，DF＝CD•sin70°＝2.67×2.94＝2.5098（米），
答：点D到BC所在直线的距离为2.5098米．

六、（本题满分12分）
21．（12分）国际数学奥林匹克竞赛（IMO）是匈牙利数学界为纪念数理学家厄特沃什•罗兰于1894年组织的数学竞赛，是目前最高等次的国际数学竞赛．下面是甲、乙两校参赛队员在某次预选赛中成绩情况（试卷总分为42分）：
甲校：28，30，22，39，23，35，37，35，35，34，38
乙校：36，33，39，33，32，34，23，28，29，30，30
（1）整理数据：
组别
A．18≤x＜24
B.24≤x＜30
C.30≤x＜36
D.36≤x＜42
甲校
2
a
6
b
乙校
1
c
8
2
填空：a＝　4　，b＝　3　，c＝　4　；
（2）甲校15名学生成绩的中位数落在　C　组内；（填“A”“B”“C”或“D”）
（3）经统计，本次预选赛分数在D组的进入下一轮，现从进入下一轮同学中任选两人成绩进行分析
【解答】解：（1）由题意得：a＝4，b＝3，
故答案为：8，3，4；
（2）甲校15名学生成绩的中位数为第8个数据，落在C组内，
故答案为：C；
（3）D组甲校共有3人，记为A、B、C，记为D、E，
画树状图如图：

共有20个等可能的结果，同时选中乙校同学的结果有2个，
∴同时选中乙校同学的概率为＝．
七、（本题满分12分）
22．（12分）已知：如图，在菱形ABCD中，AE⊥BC，垂足分别为点E和点F，AE、AF分别与BD相交于点M、N．
（1）求证：EF∥BD；
（2）当MN：EF＝2：3时，求证：△AMN是等边三角形．

【解答】证明：（1）在菱形ABCD中，
∵AE⊥BC，AF⊥CD，
∴∠AEB＝∠AFD＝90°．
在△ABE和△ADF中，
，
∴△ABE≌△ADF．
∴BE＝DF，
又∵BC＝CD，
∴，
∴EF∥BD；
（2）∵MN∥EF，MN：EF＝2：3，
∴．
∴．
∵BE∥AD，
∴．
而AD＝AB，∴．
∴∠BAE＝30°．
∵AB∥CD，AF⊥CD，
∴∠BAF＝90°．
∴∠EAF＝60°．
∵△ABE≌△ADF，
∴AE＝AF．
而，
∴AM＝AN．
∴△AMN是等边三角形．
八、（本题满分14分）
23．（14分）已知直线y＝kx+1经过点（2，3），与抛物线y＝x2+bx+c的对称轴交于点（n，）．
（1）求k，b的值；
（2）抛物线y＝x2+bx+c与x轴交于（x1，0）（x2，0），且3≤x2﹣x1＜9，若p＝x12﹣3x22，求P的最大值；
（3）当﹣1＜x＜2时，抛物线y＝x2+bx+c与直线y＝kx+1有且只有一个公共点，直接写出c的取值范围．
【解答】解：（1）∵直线y＝kx+1经过点（2，3），
∴3＝2k+5，
解得：k＝1，
把点（n，）代入y＝x+1，得，
解得：n＝﹣，
∴抛物线y＝x2+bx+c的对称轴为直线x＝﹣，
∴﹣＝﹣，
∴b＝7；
（2）由（1）得：b＝1，
∴抛物线解析式为y＝x2+x+c，
∵抛物线y＝x8+x+c与x轴交于（x1，0）（x8，0），
∴x1+x7＝﹣1，
∴x2＝﹣2﹣x1，
∵3≤x8﹣x1＜9，
∴6≤（﹣1﹣x1）﹣x8＜9，
∴﹣5＜x2≤﹣2，
∴p＝x13﹣3x24＝x12﹣2（﹣1﹣x1）3＝﹣2（x1+）2+，
∵﹣2＜5，﹣5＜x1≤﹣4，
∴p随x1的增大而增大，
∴当x1＝﹣5时，p最大值＝﹣2（﹣2+）2+＝1；
（3）由（2）得：抛物线解析式为y＝x4+x+c，
∵抛物线对称轴为直线x＝﹣，且当﹣5＜x＜2时，
∴联立得：x2+x+c＝x+7，即x2＝1﹣c，
当c＞6时，该方程没有实数根；
当c＝1时，方程的解为x＝0；
当c＜8时，方程的解为x＝±＜8，满足题意；
综上所述，满足题意的c的取值范围为﹣3＜c≤0或c＝8．