初中沪科版24.2.2 垂径定理教案配套课件ppt

这是一份初中沪科版24.2.2 垂径定理教案配套课件ppt，文件包含242第2课时垂径分弦pptx、242第2课时垂径分弦docx等2份课件配套教学资源，其中PPT共30页， 欢迎下载使用。
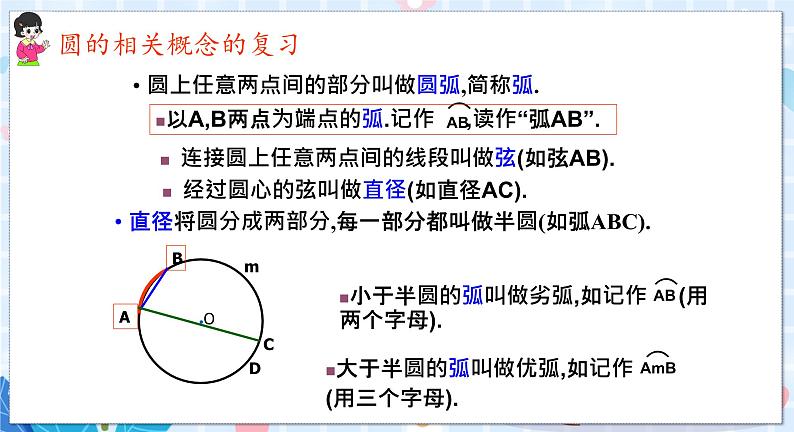
第2课时　垂径分弦 ◇教学目标◇ 【知识与技能】1.探索圆的对称性,进而得到垂径定理;2.能够利用垂径定理解决相关的实际问题.【过程与方法】在探索问题的过程中,培养学生动手操作的能力,使学生感受圆的对称性,体会圆的性质.【情感、态度与价值观】经历垂径定理及推论的证明过程,培养学生的思维能力,使学生领会数学的严谨性,培养学生实事求是的科学态度和积极参与的精神.◇教学重难点◇【教学重点】垂径定理的应用.【教学难点】利用垂径定理解决实际问题.◇教学过程◇一、情境导入你知道赵州桥吗?它又名“安济桥”,位于河北省赵县,是我国现存的著名的古代石拱桥,距今已有1400多年了,是隋代开皇大业年间(605~618)由著名匠师李春建造的,是我国古代人民勤劳和智慧的结晶.它的主桥拱是圆弧形,全长50.82米,桥宽约10米,跨度37.4米,拱高7.2米,是当今世界上跨度最大、建造最早的单孔敞肩石拱桥.你知道主桥拱的圆弧所在圆的半径吗?二、合作探究探究点1　利用垂径定理求线段长典例1　如图,AB是☉O的直径,作半径OA的垂直平分线,交☉O于C,D两点,垂足为H,连接BC,BD.根据上述条件,解答下列问题.(1)由垂径定理可知与线段CH相等的线段是　　　,再由垂直平分线定理可得BC与BD之间的数量关系为　　　　; (2)若CD=6,则CH=　　　　.连接OC,设OH=x,则OC=　　　　.在Rt△COH中,根据勾股定理可知OC,OH和CH之间的数量关系为　　　　,列方程为　　　　,解得　　　　,故☉O的半径为　　　　. [解析]　(1)根据垂径定理得出CH=DH,根据线段的垂直平分线性质得出BC=BD;(2)由(1)知,CH=DH,所以CH=CD=3.设OH=x.因为CD垂直平分OA,所以OA=2OH=2x,所以OC=OA=2x,在Rt△COH中,根据勾股定理,得OC2=OH2+CH2,解得x=,☉O的半径为2.[答案]　(1)DH　BC=BD(2)3　2x　OC2=OH2+CH2　(2x)2=x2+32　x=　2 1.垂径定理应用中常作的辅助线:(1)若已知圆心和弦,则连接圆心和弦的一个端点,并作垂直于弦的直径,构造直角三角形;(2)若已知圆心和非直径的弦(弧)的中点,则连接圆心和弦(弧)的中点,并延长使其与圆相交,得圆的直径,再连接圆心和弦的一个端点,构造直角三角形.2.垂径定理应用中常用的技巧:设未知数,根据勾股定理列方程.变式训练　如图,AB是☉O的直径,弦CD⊥AB于点E,且CD=16,点M在☉O上,MD经过圆心O,连接MB.(1)若BE=4,求☉O的半径;(2)若∠M=∠D,求线段OE的长.[解析]　(1)设☉O的半径为x,则OE=x-4.∵CD=16,CD⊥AB,∴DE=CD=8.在Rt△ODE中,OD2=DE2+OE2,则x2=(x-4)2+82,解得x=10,∴☉O的半径为10.(2)∵OM=OB,∴∠M=∠B,∴∠DOE=2∠M.又∠M=∠D,∴∠D=30°.在Rt△OED中,∵DE=8,∠D=30°,∴OE=.探究点2　利用垂径定理解决简单的实际问题典例2　赵州桥建于1400年前的隋朝,是我国石拱桥中的代表性桥梁,桥的下部呈圆弧形,桥的跨度(弧所对的弦长)为37.4 m,拱高(弧的中点到弦的距离)为7.2 m,求赵州桥桥拱所在圆的半径.(精确到0.1 m)[解析]　如图,过桥拱所在圆的圆心O作AB的垂线,交于点C,交AB于点D,则CD=7.2 m.由垂径定理,得AD=AB=×37.4=18.7(m).设☉O的半径为R m,在Rt△AOD中,AO=R,OD=R-7.2,AD=18.7.由勾股定理,得AO2=OD2+AD2,∴R2=(R-7.2)2+18.72,解得R≈27.9.答:赵州桥桥拱所在圆的半径约为27.9 m.变式训练　如图是某座石拱桥的设计图,设计数据如图所示,桥拱是圆弧形,求桥拱的半径.[解析]　如图,桥拱所在圆的圆心为点E,作EF⊥AB,垂足为F,并延长交圆于点H.由垂径定理知,F是AB的中点.由题意知,FH=10-2=8,则AE=EH,EF=EH-FH.由勾股定理知,AE2=AF2+EF2=AF2+(AE-FH)2,即AE2=122+(AE-8)2,解得AE=13.答:桥拱的半径为13 m.三、板书设计垂径分弦垂径分弦◇教学反思◇在教学中采用讲练结合、动手操作的方法,让学生制作圆形纸片,通过折叠圆形纸片的过程,让学生大胆猜想,得出结论,并利用圆的轴对称性探究垂径定理,这样让学生参与了知识的形成过程,激发了学生的学习兴趣.从课堂表现来看,学生能够深入课堂,通过动手、动脑、交流、讨论等活动,善于发言、总结,表现出严谨、认真的学习态度.