初中沪科版19.2 平行四边形教学ppt课件

这是一份初中沪科版19.2 平行四边形教学ppt课件，共25页。PPT课件主要包含了知识要点，ABCD，ACCA，∠1∠2，练一练，连接AC，BCDA已知，∵AECF，从边考虑，从角考虑等内容，欢迎下载使用。
1.一组对边平行且相等的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.对角线互相平分的四边形是平行四边形
问题2 平行四边形的性质有哪些？
问题1 平行四边形的定义是什么？
两组对边分别平行的四边形叫平行四边形.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
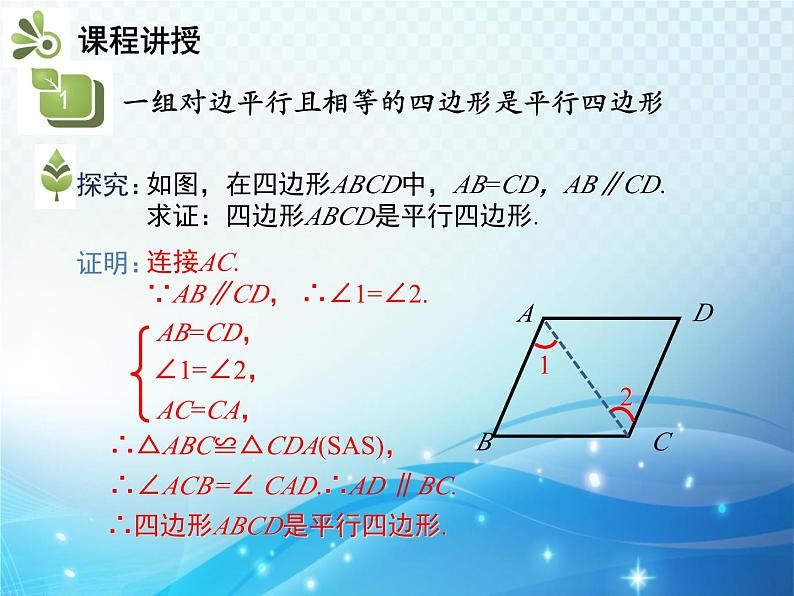
如图，在四边形ABCD中，AB=CD，AB∥CD.求证：四边形ABCD是平行四边形.
连接AC.∵AB∥CD， ∴∠1=∠2.
∴△ABC≌△CDA(SAS)，
∴∠ACB=∠ CAD.∴AD ∥BC.
∴四边形ABCD是平行四边形.
归纳：平行四边形判定定理1：一组对边平行且相等的四边形是平行四边形.数学表达式：在四边形ABCD中，∵AB∥CD, AB=CD,∴四边形ABCD是平行四边形.
例 如图，在▱ABCD中，E，F分别是AB，CD的中点.求证：四边形EBFD是平行四边形.证明：∵四边形ABCD是平行四边形，∴AB =CD，EB //FD．又 ∵EB = AB ，FD = CD，∴EB =FD ．∴四边形EBFD是平行四边形．
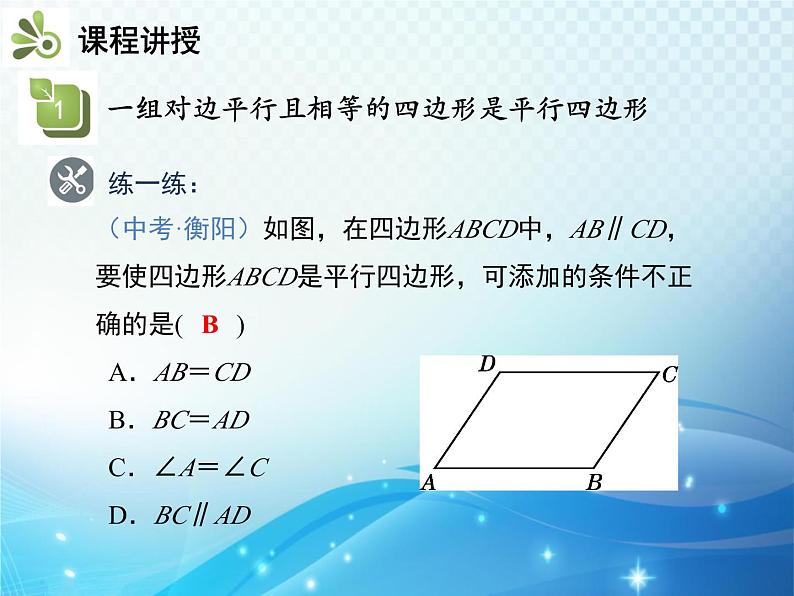
（中考·衡阳）如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，可添加的条件不正确的是(　　) A．AB＝CD B．BC＝AD C．∠A＝∠C D．BC∥AD
归纳：要证四边形是平行四边形，已知有一组对边平行，联想的思路有两种：一是证明另一组对边平行；二是证明平行的这组对边相等．而证明边相等要三角形全等这条思路较常见．
在四边形ABCD中，AB=DC，AD=BC.求证： 四边形ABCD是平行四边形.
在△ABC和△CDA中,
AB=CD (已知)，
AC=CA (公共边)，
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3，
∴AB∥ CD , AD∥ BC，
归纳：平行四边形判定定理2：两组对边分别相等的四边形是平行四边形；数学表达式：如图，∵AB＝CD，AD＝BC，∴四边形ABCD是平行四边形.
如图，分别以△ABC的三边为一边，在BC的同侧 作等边三角形ABD，等边三角形BCE，等边三角 形ACF，连接DE，EF. 求证：四边形ADEF是平行四边形．
∵△ABD，△BCE，△ACF都为等边三角形，∴DB＝AB＝AD，BE＝BC，AC＝AF，∠DBA＝60°，∠EBC＝60°.∴∠DBE＝60°－∠EBA，∠ABC＝60°－∠EBA， ∴∠DBE＝∠ABC，∴△DBE≌△ABC，∴DE＝AC.又∵AC＝AF，∴AF＝DE.同理可证：△ABC≌△FEC，∴AB＝FE，∴FE＝AD，∴四边形ADEF是平行四边形．
四边形ABCD中，OA=OC，OB=OD.求证：四边形ABCD是平行四边形.
∵OA=OC，OD=OB, ∠AOD=∠COB， ∴△ AOD≌△COB， ∴∠OAD=∠OCB. ∴AD//BC. 同理得AB//DC. ∴四边形ABCD是平行四边形.
归纳：平行四边形判定定理3：对角线互相平分的四边形是平行四边形.数学表达式：在四边形ABCD中，∵AO=CO,DO=BO,∴四边形ABCD是平行四边形.
例 已知：点E，F是平行四边形ABCD的对角线AC上两点，且AE=CF. 求证：四边形BEDF是平行四边形.
证明：连接BD交AC与点O,
因为四边形ABCD是平行四边形，所以AO=CO，BO=DO
∴OE=AO-AE=CO-CF=FO.
∴ 四边形BEDF是平行四边形.
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理2)
一组对边平行且相等的四边形是平行四边形（判定定理1）
两组对角分别相等的四边形是平行四边形（定义拓展）
对角线互相平分的四边形是平行四边形（判定定理3）
1. 四边形的四条边长分别是a，b，c，d，其中a，b为 一组对边长，c，d为另一组对边长且a2＋b2＋c2＋d2＝2ab＋2cd，则这个四边形是(　　) A．任意四边形 B．平行四边形 C．对角线相等的四边形 D．对角线垂直的四边形
2. 下列给出的条件中，能判定四边形ABCD是平行 四边形的是(　　) A．AB∥CD，AD＝BC 　B．AB＝AD，CB＝CD C．AB＝CD，AD＝BC 　 D．∠B＝∠C，∠A＝∠D
3.(中考·湘西)下列说法错误的是(　　) A．对角线互相平分的四边形是平行四边形 B．两组对边分别相等的四边形是平行四边形 C．一组对边平行且相等的四边形是平行四边形 D．一组对边相等，另一组对边平行的四边形是 平行四边形
4.如图，在▱ABCD中，点E，F分别在AD，BC上，若要使四边形AFCE是平行四边形，可以添加的条件是(　　)①AF＝CF；②AE＝CE；③BF＝DE；④AF∥CE. A．①或②　 B．②或③ C．③或④　 D．①或③
5.如图，在四边形ABCD中，
(1)如果AB∥CD，AD∥BC，那么四边形ABCD是 ___________.(2)如果∠A：∠B：∠ C：∠D=a：b：a：b(a,b为正 数),那么四边形ABCD是__________ .
(3)如果AD=6 cm,AB=4 cm,那么当BC=_______cm, CD=_____cm时,四边形ABCD为平行四边形.
6.如图，AB，CD相交于点O，AC∥DB，AO＝BO，E ， F 分别是OC，OD的中点．求证：(1)△AOC≌△BOD；(2)四边形AFBE是平行四边形．
证明：(1)∵AC∥BD，∴∠C＝∠D.又∵∠COA=∠DOB，AO＝BO ，∴△AOC≌△BOD(AAS)；(2)∵△AOC≌△BOD，∴CO＝DO.∵E ， F分别是OC ， OD的中点，∴EO＝FO.又∵AO＝BO，∴四边形AFBE是平行四边形．
7.如图，在平行四边形ABCD中，点E，F分别在AB，CD上，AE=CF，连接AF，BF，DE，CE，分别交于H，G．求证：（1）四边形AECF是平行四边形；（2）EF与GH互相平分．证明：（1）∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∵AE=CF，∴四边形AECF是平行四边形．
（2）由（1），得四边形AECF是平行四边形，∴AF∥CE，∵AE=CF，AB∥CD，AB=CD，∴BE∥DF，BE=DF，∴四边形BFDE是平行四边形，∴BF∥DE，∴四边形EGFH是平行四边形，∴EF与GH互相平分．