沪科版八年级下册19.3 矩形 菱形 正方形教学课件ppt

这是一份沪科版八年级下册19.3 矩形 菱形 正方形教学课件ppt，共19页。PPT课件主要包含了知识要点，对边平行且相等，四个角都是直角，练一练等内容，欢迎下载使用。

1.对角线相等的平行四边形是矩形
2.有三个角是直角的四边形是矩形
问题2 矩形的性质有哪些？
问题1 矩形的定义是什么？
有一个角是直角的平行四边形叫做矩形.
对角线互相平分且相等.
想一想：我们知道，矩形的对角线相等.反过来，对角线相等的平行四边形是矩形吗？ 工人师傅在做门窗或矩形零件时，不仅要测量两组对边的长度是否分别相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形.你知道其中的道理吗？
如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.求证：□ABCD是矩形.证明：∵AB = DC,BC = CB,AC = DB, ∴ △ABC≌△DCB , ∴∠ABC = ∠DCB. ∵AB∥CD, ∴∠ABC + ∠DCB = 180°, ∴ ∠ABC = 90°, ∴ □ ABCD是矩形（矩形的定义）.
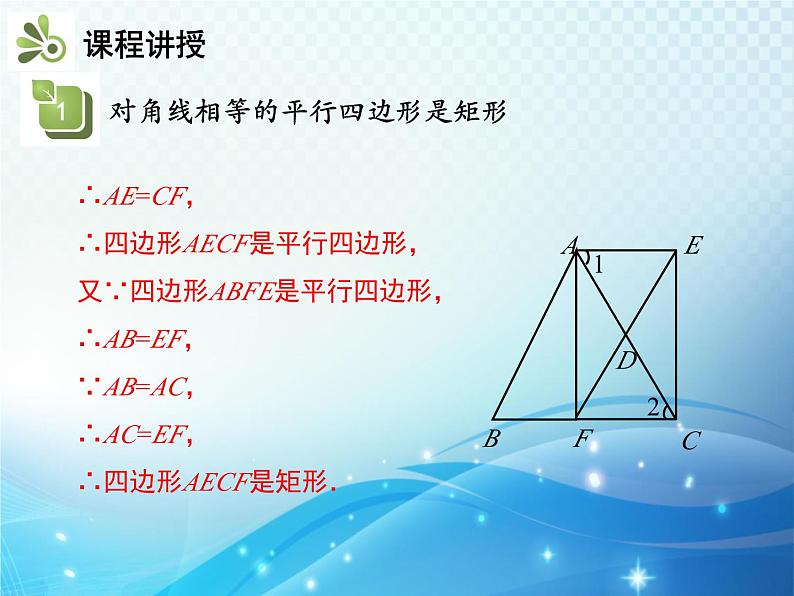
　 例 已知，如图在△ABC中，AB=AC，点D是AC的中点，直线AE ∥ BC，过D点作直线EF ∥ AB分别交AE，BC于点E，F，求证：四边形AECF是矩形．
证明：∵AE ∥ BC，∴∠1=∠2，在△ADE和△CDF中， ∵∠1=∠2，∠ADE=∠CDF，AD=CD，∴△ADE≌△CDF.
∴AE=CF，∴四边形AECF是平行四边形，又∵四边形ABFE是平行四边形，∴AB=EF，∵AB=AC，∴AC=EF，∴四边形AECF是矩形．
如图，要使▱ABCD成为矩形，需添加的条件是(　　) A．AB＝BC B．AO＝BO C．∠1＝∠2 D．AC⊥BD
如图，在四边形ABCD中，∠A=∠B=∠C=90°.求证：四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°，∴∠A+∠B=180°，∠B+∠C=180°，∴AD∥BC，AB∥CD.∴四边形ABCD是平行四边形，∴四边形ABCD是矩形.
如图，在平行四边形ABCD中，AE=CF，AG⊥DE，CH⊥BF，求证：四边形EHFG是矩形．
证明：∵四边形ABCD是平行四边形，∴AE∥CF ．∵AE=CF，∴四边形AECF是平行四边形，∴AF∥EC，∴∠FGE+∠GEH=180°.又∵AG⊥DE，CH⊥BF，∴∠FGE=∠EHF=90°，∴∠GEH=90°∴四边形EHFG是矩形．
1.下列命题中，真命题有(　　)(1)对角线互相平分的四边形是矩形(2)三个角的度数之比为1：3 ：4的三角形是直角三角形(3)对角互补的平行四边形是矩形(4)三边之比为1： ：2的三角形是直角三角形 A．1个 B．2个 C．3个 D．4个
2.如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是(　　) A．AB∥DC B．AC＝BD C．AC⊥BD D．AB＝DC
3.（中考·龙东）如图，在▱ABCD中，延长AD到点E，使DE＝AD，连接EB，EC，DB，请你添加一个条件______________________，使四边形DBCE是矩形．
EB＝DC(答案不唯一)
4.如图，在△ABC中，AB＝AC，AD是BC边上的高，AE是△BAC的外角平分线，DE∥AB交AE于点E，求证：四边形ADCE是矩形．
证明：∵AB＝AC，AD⊥BC，∴∠B＝∠ACB，BD＝DC.∵AE是∠BAC的外角平分线，∴∠FAE＝∠EAC.∵∠B＋∠ACB＝∠FAE＋∠EAC，∴∠B＝∠ACB＝∠FAE＝∠EAC， ∴AE∥CD.又∵DE∥AB，∴四边形AEDB是平行四边形，∴AE BD.又∵BD＝DC，∴AE DC，∴四边形ADCE是平行四边形.又∵∠ADC＝90°，∴平行四边形ADCE是矩形．