




初中数学沪科版八年级下册19.3 矩形 菱形 正方形图文课件ppt
展开正方形的定义正方形的性质正方形的判定
1.正方形的定义 有一个角是直角,且有一组邻边相等的平行四边形叫做正方形 .
特别提醒1. 正方形必须具备的两个条件 :(1)四条边相等 .(2)四个角都是直角 .2. 正方形的四条边都相等,说明正方形既是平行四边形,又是菱形;正方形的四个角都是直角,说明正方形是矩形,即正方形不仅是平行四边形,也是矩形和菱形.
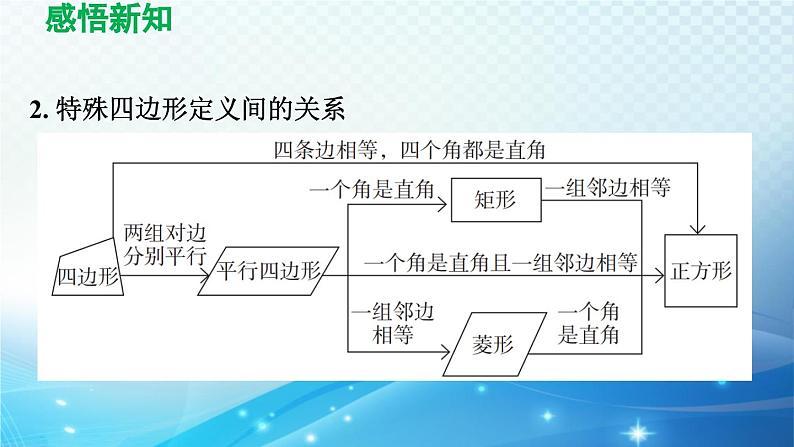
2. 特殊四边形定义间的关系
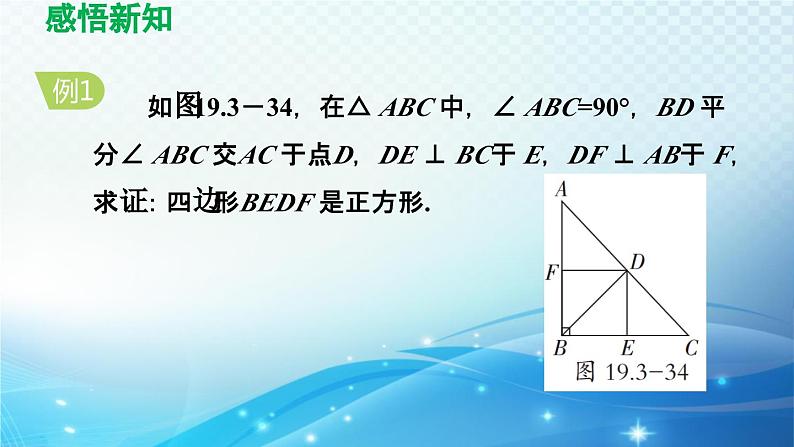
如图19.3-34,在△ ABC 中,∠ ABC=90°,BD 平分∠ ABC 交AC 于点D,DE ⊥ BC于 E,DF ⊥ AB于 F,求证:四边形BEDF 是正方形.
解题秘方:紧扣定义中“四条边都相等,四个角都是直角的四边形是正方形”进行判定.
证明: ∵ DE ⊥ BC,DF ⊥ AB,∠ ABC=90°,∴∠ DEB=∠ EBF=∠ BFD=90°.∴四边形BEDF 是矩形.∴∠ DEB= ∠ EBF= ∠ BFD= ∠ FDE=90°,BE=FD,BF=ED.∵ BD 平分∠ ABC,DE ⊥ BC,DF ⊥ AB,∴ DE=DF. ∴ DE=DF=BF=BE. ∴四边形BEDF 是正方形.
解法提醒利用正方形定义判定正方形,它是建立在四边形的基础上,因此,既要有四条边相等,又要有四个角都是直角,两者缺一不可 .
1.正方形的性质 具有矩形、菱形、平行四边形的一切性质,即:(1) 边: 四条边相等,邻边垂直,对边平行;(2) 角: 四个角都是直角;
(3) 对角线: 对角线相等,互相垂直平分,每条对角线平分一组对角;(4) 是轴对称图形,有 4 条对称轴;(5) 面积为边长的平方或对角线长平方的一半 .
2. 特殊四边形的性质间的关系
特别提醒1. 矩形、菱形、正方形都是特殊的平行四边形,它们之间的关系如图19.3-35所示.
2.正方形的特殊性质:(1) 正方形的一条对角线把正方形分成两个全等的等腰直角三角形;两条对角线把正方形分成四个全等的小等腰直角三角形;(2) 周长相等的四边形中,正方形的面积最大 .
解题秘方:从正方形中获取边、角相等的信息.
如图 19.3-36 所示,在正方形ABCD 中,E 为CD 上一点,F为BC 延长线上一点,CE=CF.
解法提醒利用正方形的性质解题,由于正方形的性质较多,解题时不宜一一列出来,需要根据题中已知条件,结合要证明的结论,选择证明结论成立所需要的性质,使解题思路更简洁.
(1)求证:△ BCE ≌△ DCF;
证明:∵四边形ABCD 是正方形,∴ BC=DC,∠ BCE= ∠ DCF=90° .又∵ CE=CF,∴△ BCE ≌△ DCF.
(2)若∠ BEC=60°,求∠ EFD 的度数.
解:∵△ BCE ≌△ DCF,∠ BEC=60°,∴∠ DFC= ∠ BEC=60° .∵ CE=CF,∠ ECF=90°,∴∠ CFE=45° .∴∠ EFD=∠ DFC- ∠ CFE=60°-45°=15°.
1. 判定方法(1) 从四边形出发: ①四条边相等,四个角都是直角的四边形是正方形;②对角线互相平分、垂直且相等的四边形是正方形;(2)从平行四边形出发: ①有一组邻边相等并且有一个角是直角的平行四边形是正方形;②对角线互相垂直且相等的平行四边形是正方形;
(3)从矩形出发: ①有一组邻边相等的矩形是正方形;②对角线互相垂直的矩形是正方形;(4)从菱形出发: ①有一个角是直角的菱形是正方形;②对角线相等的菱形是正方形 .
2. 四边形间的关系 四边形、平行四边形、矩形、菱形、正方形间的转化关系如下所示 .
特别提醒常见的判定思路:从边上证明. 矩形 正方形;从角上证明.菱形 正方形;
从对角线上证明.(1)矩形 正方形;(2)菱形 正方形;(3)平行四边形 正方形;(4)四边形 正方形;
对角线相等且互相垂直平分
如图 19.3 - 37,已知在正方形 ABCD 中,对角线 AC与 BD 交于点 O,点 E, F, G, H 分别在 AB, AD, DC, BC上,若 EG,FH 均过点 O,且 EG ⊥ FH. 求证:四边形 EFGH是正方形 .
解题秘方:紧扣正方形的几种判定方法,找准切入点是解决问题的关键 .
证明: ∵四边形 ABCD 为正方形,∴ OB=OC,∠ ABO= ∠ BCO=45°,∠ BOC=90° = ∠ COH+∠ BOH.∵ EG ⊥ FH,∴∠ BOE+ ∠ BOH=90°,∴∠ COH= ∠ BOE,∴△ CHO ≌△ BEO, ∴ OH=OE.同理可得 OE=OF=OG=OH,∴ OE+OG=OF+OH,即 EG=HF.又 EG ⊥ FH,∴四边形 EFGH 为正方形 .
方法点拨判定四边形是正方形的方法1. 如果已知条件是平行四边形,需证它既是矩形又是菱形;2. 如果已知条件是四边形,若按边角关系证明,则需证它的四条边相等,四个角是直角;若按特殊四边形证明,则要先证它是平行四边形,再证它既是矩形又是菱形
3. 如果已知条件是矩形,再证它的邻边相等或对角线互相垂直即可;4. 如果已知条件是菱形,再证它有一个角是直角或对角线相等即可.
初中数学沪科版八年级下册19.3 矩形 菱形 正方形作业ppt课件: 这是一份初中数学沪科版八年级下册19.3 矩形 菱形 正方形作业ppt课件,共58页。
数学八年级下册19.3 矩形 菱形 正方形评课ppt课件: 这是一份数学八年级下册19.3 矩形 菱形 正方形评课ppt课件,共15页。PPT课件主要包含了复习回顾,探究新知,典型例题,小试身手等内容,欢迎下载使用。
数学八年级下册19.3 矩形 菱形 正方形教课内容ppt课件: 这是一份数学八年级下册19.3 矩形 菱形 正方形教课内容ppt课件,共27页。PPT课件主要包含了平行四边形再认识,复习回顾,正方形的定义,引入新知,正方形的性质,边----,角----,对角线----,对称性----,识别正方形的方法等内容,欢迎下载使用。













