2023届天津市新华中学高三下学期统练（3）数学试题含解析

2023届天津市新华中学高三下学期统练（3）数学试题

一、单选题

1．已知集合，则（    ）

A． B． C． D．

【答案】A

【分析】先求出集合A,B,然后取交集即可.

【详解】,

则,

故选：A

2．“”是 “”的

A．充分不必要条件； B．必要不充分条件；

C．充要条件； D．既不充分也不必要条件.

【答案】A

【详解】，而，如，则不成立，所以”是 “”的充分不必要条件．选.

【解析】充分条件、必要条件.

3．为了了解小学生的体能情况，抽取了某小学四年级100名学生进行一分钟跳绳次数测试，将所得数据整理后，绘制如下频率分布直方图.根据此图，下列结论中错误的是（    ）

A．

B．估计该小学四年级学生的一分钟跳绳的平均次数超过125

C．估计该小学四年级学生的一分钟跳绳次数的中位数约为119

D．四年级学生一分钟跳绳超过125次以上优秀，则估计该小学四年级优秀率为35%

【答案】B

【分析】根据频率分布直方图矩形面积和等于1可得，经计算可得平均数为，中位数约为119，优秀率为35%即可得出正确选项.

【详解】根据题意可得，可得，故A正确；

根据频率分布直方图可得其平均数为

，所以B错误；

由频率分布直方图可知，，而，

所以中位数落在区间内，设中位数为，则，可得，所以C正确；

由图可知，超过125次以上的频率为，所以优秀率为35%，即D正确.

故选：B

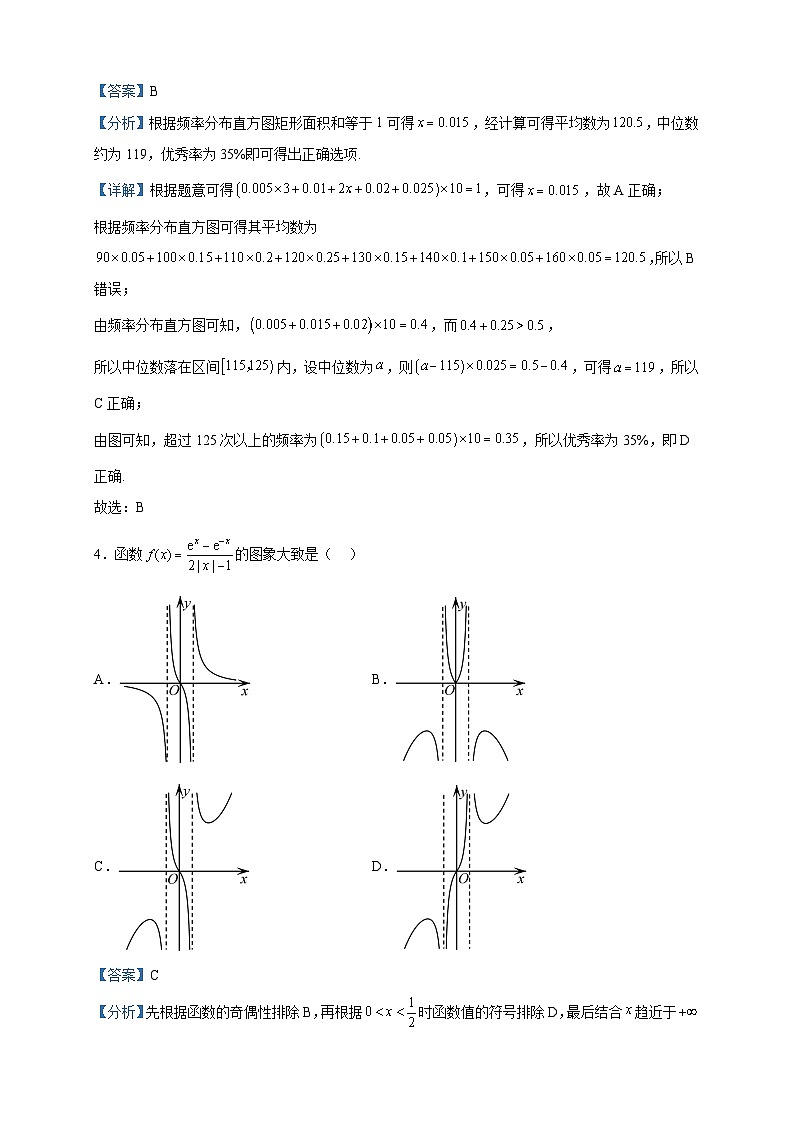
4．函数的图象大致是（    ）

A． B．

C． D．

【答案】C

【分析】先根据函数的奇偶性排除B，再根据时函数值的符号排除D，最后结合趋近于时函数值的范围求解即可.

【详解】解：函数的定义域为，，

所以函数为奇函数，图像关于原点对称，排除B选项，

因为当时，，

所以当时，，时，，故排除D，

当趋近于时，由于指数呈爆炸型增长，故函数值趋近于，故排除A选项，

故选：C

5．设，，，则，，的大小关系是（    ）

A． B．

C． D．

【答案】A

【分析】根据指数函数，对数函数的性质，借助“”与“”，即可判断大小关系.

【详解】因为，，

所以

故选:A

6．设双曲线C：（，）的左焦点为F，直线过点F且与双曲线C在第二象限的交点为P，，其中O为坐标原点，则双曲线C的方程为（    ）

A． B．

C． D．

【答案】D

【分析】将左焦点坐标代入中可求出，设右焦点为N，连接，，，则三角形为直角三角形，可得，，然后利用双曲线的定义列方程可求出，从而可求出双曲线的方程

【详解】设左焦点F的坐标为，由点F过直线，

所以，解得，

设右焦点为N，连接，，.

由，故三角形为直角三角形，即,

又因为直线斜率为，设直线倾斜角为，则.

又，则，，

由双曲线定义，则，

所以，

所以

所以双曲线C的方程为.

故选：D.

7．足球起源于中国古代的蹴鞠游戏．“蹴”有用脚蹴、踢的含义，“鞠”最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，已知某“鞠”的表面上有四个点，满足，面ABC，⊥，若，则该“鞠”的体积的最小值为（    ）

A． B． C． D．

【答案】B

【分析】作出辅助线，找到球心的位置，得到PB为球的直径，推导出要想该“鞠”的体积最小，只需AB最小，由得到，结合基本不等式，求出最小值，从而得到直径最小值，求出体积最小值.

【详解】因为，面ABC，⊥，

故AB为三角形ABC所在小圆的直径，取AB中点，过作，交BP于点O，则O即为球心，PB为球的直径，

要想该“鞠”的体积最小，只需PB最小，由于，

故只需AB最小，其中，

故，

解得：，

由基本不等式得：，当且仅当时，等号成立，

故最小值为2，此时直径最小值为，

所以该“鞠”的体积最小值为.

故选：B

【点睛】解决与球有关的内切或外接的问题时，解题的关键是确定球心的位置．对于外切的问题要注意球心到各个面的距离相等且都为球半径；对于球的内接几何体的问题，注意球心到各个顶点的距离相等，解题时要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形，利用勾股定理求得球的半径.

8．已知函数，则下列结论中正确的是（    ）

A．函数的最小正周期为

B．时取得最大值

C．的对称中心坐标是（）

D．在上单调递增

【答案】D

【分析】根据正弦型函数的图象与性质，对各选项逐一分析即可求解.

【详解】解：，

对A：函数的最小正周期为，故选项A错误；

对B：因为，所以，且，故选项B错误；

对C：令，，得，

所以的对称中心坐标是，，故选项C错误；

对D：因为，所以，

又在上单调递增，所以在上单调递增，故选项D正确.

故选：D.

9．已知函数若方程恰有四个不同的实数解，分别记为，则的取值范围是（    ）

A． B． C． D．

【答案】A

【分析】当时利用辅助角公式化简函数解析，再画出函数图象，不妨令，则，且与关于对称，再根据对数的运算得到，最后转化为关于的函数，结合对勾函数的性质计算可得；

【详解】解：，

当时

令，解得，当时，

当时，令，解得或，

令，解得或，

函数的图象如下所示：

因为方程恰有四个不同的实数解，即与恰有四个交点，所以，

不妨令，则，且与关于对称，所以，

又，即，所以，即，

所以，

所以，

因为在上单调递增，所以，

所以；

故选：A

二、填空题

10．已知复数z满足（其中i为虚数单位），则复数z的共轭复数为___________.

【答案】

【分析】利用复数代数形式的乘除运算和模长公式进行化简，再由共轭复数的基本概念即可得出结果.

【详解】由，

得，

则复数z的共轭复数为

故答案为：

三、双空题

11．若展开式中的所有项系数和为243，则_______；该展开式中的系数___________.

【答案】         

【分析】令，结合所有项系数的和即可求出，再求出展开式的通项，令的指数等于，即可得解.

【详解】令，则，解得，

则的展开式的通项为，

令，得，

∴展开式中的系数为.

故答案为：；.

四、填空题

12．已知圆的圆心到直线的距离为1，则圆C截直线l所得弦长为________.

【答案】或

【分析】配方得圆的圆心为，半径，利用点到直线距离公式求得a值，利用勾股定理代入可得弦长.

【详解】由题意配方得，圆的圆心为，

圆心到直线l：的距离为

解得或，

当时，半径为2，所以弦长为，

当时，半径为，所以弦长为，

故答案为：2或.

13．已知实数满足，则的最大值为___________．

【答案】

【分析】法八：利用基本不等式，即可求解.

【详解】[方法一]：（代换，用判别式法）

设，则，代入，

得，由得，因此.

[方法二]：（代换，构造一元二次方程用判别式法）

设，则，则2x、y可看作关于m的方程的两个实根，由得，因此.

[方法三]：（构造向量法）

令，.

则，即的最大值为.

[方法四]：（待定系数法）

令

则解得故，化简得.

［方法五］：（代换消项结合放缩法）

令，则，则原题等价于：已知，求2a的最大值.

由的几何意义得，即得.即.

［方法六］：（换元法，转化为三角函数求解）

令则.

即，即，则.

.

故.

［方法七］：（三角换元结合均值不等式求解）

令代入条件方程得.

则.

故.

故答案为：．

［方法八］：【最优解】基本不等式

，

即，(当且仅当，即时，取等号)

故答案为：．

【整体点评】法一：换元利用判别式法求出；

法二：代换构造一元二次方程根据判别式法求出；

法三：构造向量利用求出；

法四：构造平方和，利用平方数自身的范围求出；

法五：代换利用椭圆的几何性质求出；

法六：利用三角代换求出，是该类型题的常用方式；

法七：利用三角代换结合基本不等式求出；

法八：直接利用基本不等式，是该题的通性通法，也是最优解．

五、双空题

14．甲箱中有5个红球，2个白球和3个黑球，乙箱中有4个红球，3个白球和3个黑球．先从甲箱中随机取出1球放入乙箱中，分别以、、表示由甲箱中取出的是红球，白球和黑球的事件；再从乙箱中随机取出一球，以表示由乙箱中取出的球是红球的事件，则___________；若随机从甲箱中取出3个球，设取到红球个数为随机变量X，则X的数学期望为___________．

【答案】          /

【分析】由题意可得、、是两两互斥的事件，则，利用条件概率的概率公式求出即可，由题意可得X的取值可能为0，1，2，3，求出相应的概率，从而可求出X的数学期望

【详解】由题意可得、、是两两互斥的事件，，

若从甲箱中随机取出1红球放入乙箱中，则此时乙箱中有11个球，且其中5个是红球，

所以，同理可得，

所以

，

题意可得X的取值可能为0，1，2，3，则

，

，

，

，

所以,

故答案为：，

六、填空题

15．已知D是的边BC上一点，且，，，则的最大值为______．

【答案】/

【分析】设，，，则，，再在和中分别列出余弦定理，根据联立可得，再结合，得到，进而消去，结合基本不等式 求解最大值即可

【详解】

设，，，则，．

在中，；

在中，．

因为，所以，

所以，整理①．

因为，所以．

在中，，

即，结合①可得，所以，即，当且仅当时，等号成立．

故答案为：

七、解答题

16．在△ABC中，角A，B，C的对边分别为a，b，c，且

(1)求B的大小；

(2)若，求△ABC的面积.

(3)已知，且α为锐角，求的值.

【答案】(1)

(2)

(3)

【分析】（1）根据正弦定理化边为角，再根据三角形内角和定理结合两角和的正弦公式化简，即可得解；

（2）先利用余弦定理求出，再根据三角形的面积公式即可得解；

（3）先利用平方关系求出，再根据结合诱导公式即可得解.

【详解】（1）∵，

∴由正弦定理可得，

又

∴

∵，∴

∵，∴；

（2）∵，

∴由余弦定理可得，整理可得，

又，解得，

∴；

（3）因为α为锐角，所以

又因为

所以为钝角，

则

.

17．如图，平面ABCD，，，，，点E，F，M分别为AP，CD，BQ的中点.

(1)求证：平面CPM；

(2)求平面QPM与平面CPM夹角的大小；

(3)若N为线段CQ上的点，且直线DN与平面QPM所成的角为，求N到平面CPM的距离.

【答案】(1)证明见解析

(2)

(3)

【分析】（1）连接EM，证得，利用线面平行判定定理即可证明平面MPC；

（2）根据条件建立空间直角坐标系，求得平面PMQ和平面MPC法向量，利用向量的夹角公式，即可求解.

（3）设，则，从而，由（2）知平面PMQ的法向量为，利用向量的夹角公式，得到关于的方程，求出，进而得到，利用点到平面距离公式求出答案.

【详解】（1）证明：连接EM，因为，，

所以，

又因为，所以四边形PABQ为平行四边形，

因为点E和M分别为AP和BQ的中点，所以且，

因为，，F为CD的中点，所以且，

可得且，即四边形EFCM为平行四边形，

所以，又平面MPC，平面MPC，

所以平面MPC.

（2）因为平面ABCD，，故以D为原点，分别以DA，DC，DP所在的直线为x轴，y轴，z轴建立空间直角坐标系，

依题意可得，，，，，，，

，，，，

设为平面PQM的法向量，

则，不妨设，可得，

设为平面PMC的法向量，

则，不妨设，可得.

所以，

设平面PQM与平面PMC夹角为，

所以，

即平面PQM与平面PMC夹角的正弦值为.

（3）设，即，

则.

从而.

由（2）知平面PMQ的法向量为，

而直线DN与平面PMQ所成的角为，

所以，

即，

整理得，解得或，

因为，

所以，所以，，

由（2）知：为平面的法向量，

故点N到平面CPM的距离为.

18．已知椭圆上右顶点到右焦点的距离为，且右焦点到直线的距离等于短半轴的长.

(1)求椭圆C的方程；

(2)设P（4，0），AB是椭圆C上关于x轴对称的任意两个不同的点，连接PB交椭圆C于另一点E，证明直线AE与x轴相交于定点Q；

(3)在（2）的条件下，过点Q的直线与椭圆C交于M、N两点，求的取值范围.

【答案】(1)

(2)证明见解析

(3)[-4，]

【分析】（1）利用椭圆的定义和性质解出、、，即可得解；

（2）利用点斜式方程得出直线的方程，与椭圆的方程联立，利用根与系数之间的关系得出点、的坐标之间的关系，再利用点斜式表示直线的方程，进而即可证明过定点；

（3）分类讨论直线是否与轴垂直，与椭圆方程联立得出点的坐标之间的关系，再表示出，进而即可求出其取值范围．

【详解】（1）由题意可得解得，

椭圆的方程为；

（2）由题意直线的斜率存在，设直线的方程为，，

则，

联立，消去得，

直线与椭圆有两个不同的交点，

，

，．

直线的方程为，

令，

则，

故直线过定点；

（3）①当直线与轴重合时，，，；

②当直线与轴不重合时，设直线的方程为，，，

联立消去得，

则恒成立，

可得，，

，

，，，

的取值范围是，

综上可知：的取值范围是．

【点睛】方法点睛：一是利用几何方法，即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是利用代数方法，即把要求最值的几何量或代数表达式表示为某个（些）参数的函数（解析式），然后利用函数方法、不等式方法等进行求解．

19．已知等差数列{}满足，为等比数列{}的前n项和，.

(1)求{}，{}的通项公式；

(2)设，证明：.

【答案】(1)；

(2)证明见解析

【分析】（1）等差数列{}的公差设为d，等比数列的公比设为q，运用通项公式，解方程可得首项和公差、公比，进而得到所求：

（2）求得，分别运用错位相减求和，以及放缩和裂项求和证明不等式.

【详解】（1）等差数列{}的公差设为d，

，可得，解得，

可得；

由得

两式相减整理得，可得公比；

由，解得，

∴

（2）由（1）知，

设，，

两式相减整理得，

可得，

又因为，

∴.

所以，

∴.

20．已知函数

(1)当时，求曲线在点处的切线方程；

(2)若在区间各恰有一个零点，求a的取值范围．

【答案】(1)

(2)

【分析】（1）先算出切点,再求导算出斜率即可

（2）求导,对分类讨论,对分两部分研究

【详解】（1）的定义域为

当时,,所以切点为,所以切线斜率为2

所以曲线在点处的切线方程为

（2）

设

若,当,即

所以在上单调递增,

故在上没有零点,不合题意

若,当,则

所以在上单调递增所以,即

所以在上单调递增,

故在上没有零点,不合题意

若

(1)当,则,所以在上单调递增

所以存在,使得,即

当单调递减

当单调递增

所以

当,

令则

所以在上单调递增，在上单调递减，所以，

又，，

所以在上有唯一零点

又没有零点,即在上有唯一零点

(2)当

设

所以在单调递增

所以存在,使得

当单调递减

当单调递增,

又

所以存在,使得,即

当单调递增,当单调递减，

当，，

又，

而,所以当

所以在上有唯一零点,上无零点

即在上有唯一零点

所以,符合题意

所以若在区间各恰有一个零点,求的取值范围为

【点睛】方法点睛：本题的关键是对的范围进行合理分类，否定和肯定并用，否定只需要说明一边不满足即可，肯定要两方面都说明.