6.6 一次函数、一元一次方程和一元一次不等式 课件

这是一份6.6 一次函数、一元一次方程和一元一次不等式 课件，共16页。

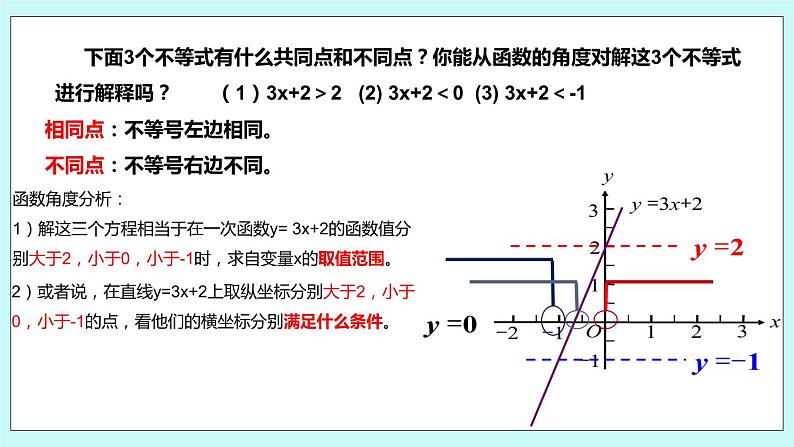
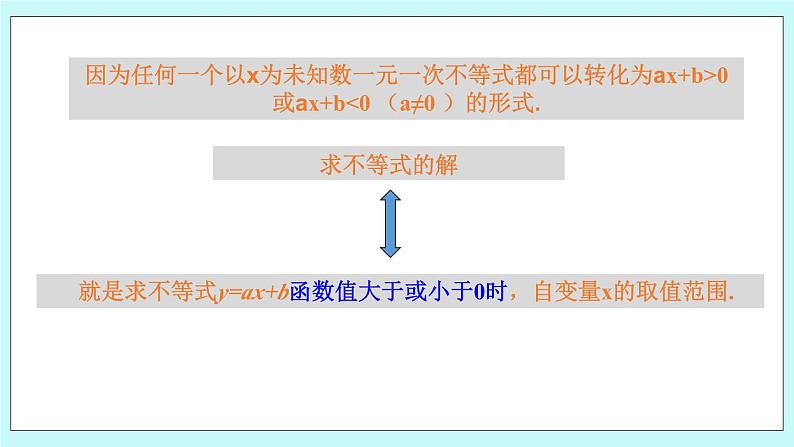
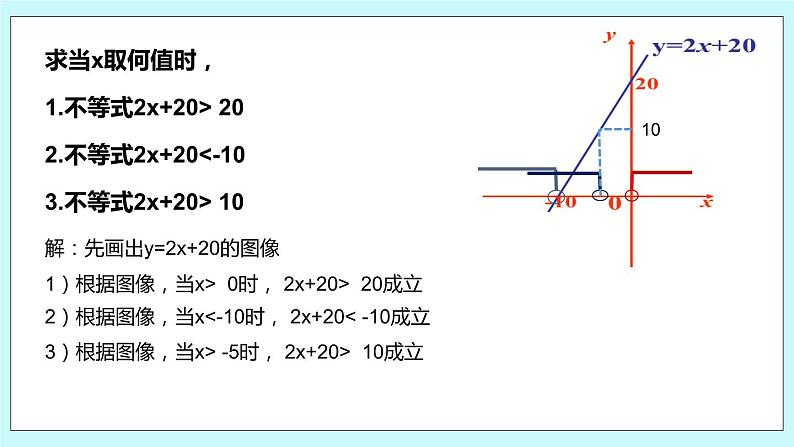
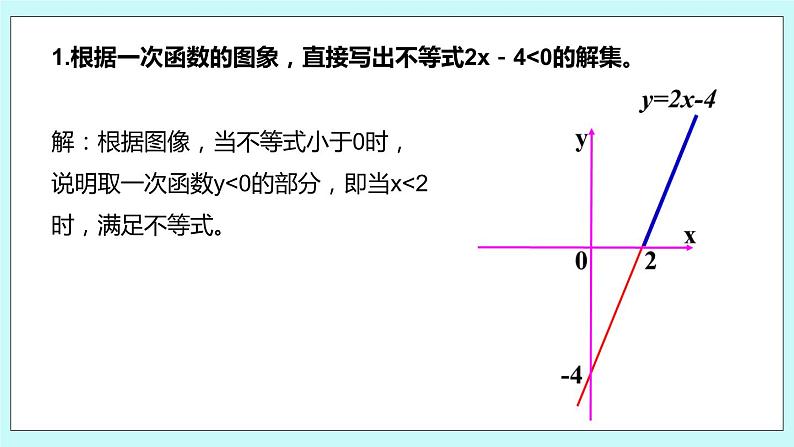
第六章 一次函数6.6 一次函数、一元一次方程和一元一次不等式学习目标1、借助图像，使学生理解一次函数与一元一次不等式的关系；2、能根据一次函数的图像求不等式的解集。重点初步理解二元一次方程与一次函数的关系。难点通过探索二元一次方程组的图象解法体会数形结合的数学思想。 一根长25cm的弹簧，一端固定，另一端挂物体。在弹簧伸长后的长度不超过35cm的限度内，每挂1kg质量的物体，弹簧伸长0.5cm。设所挂物体的质量为x kg，弹簧的长度为y cm。问题一：写出y与x之间的函数表达式，并画出函数图像？问题二 : 有一物体的质量是30 kg ，能挂在这根弹簧上吗？问题三：求这根弹簧在所允许的限度内所挂物体的最大质量。y=0.5x+252）当x=30kg，则y=0.5x+25=0.5×30+25=40<35所挂质量超过了弹簧限度，不能挂在这根弹簧上。3）当y=35 cm，则0.5x+25=35，解得x=20kg，则在允许范围内弹簧所挂物体最大质量为20kg 下面3个不等式有什么共同点和不同点？你能从函数的角度对解这3个不等式进行解释吗？ （1）3x+2＞2 (2) 3x+2＜0 (3) 3x+2＜-1相同点：不等号左边相同。不同点：不等号右边不同。函数角度分析：1）解这三个方程相当于在一次函数y= 3x+2的函数值分别大于2，小于0，小于-1时，求自变量x的取值范围。2）或者说，在直线y=3x+2上取纵坐标分别大于2，小于0，小于-1的点，看他们的横坐标分别满足什么条件。因为任何一个以x为未知数一元一次不等式都可以转化为ax+b>0或ax+b<0 （a≠0 ）的形式.求不等式的解 就是求不等式y=ax+b函数值大于或小于0时，自变量x的取值范围.求当x取何值时，1.不等式2x+20> 202.不等式2x+20<-103.不等式2x+20> 10解：先画出y=2x+20的图像1）根据图像，当x> 0时， 2x+20> 20成立2）根据图像，当x<-10时， 2x+20< -10成立3）根据图像，当x> -5时， 2x+20> 10成立10 已知一次函数的表达式，当其中一个变量的值确定时，可以由相应的一元一次方程确定另一个变量的值；当其中一个变量的取值范围确定时，可以由相应的一元一次不等式确定另一个变量的取值范围.1.根据一次函数的图象，直接写出不等式2x－4<0的解集。解：根据图像，当不等式小于0时，说明取一次函数y<0的部分，即当x<2时，满足不等式。2.根据图象,写出图象所对应的一元一次不等式及不等式的解集。由图可知，当-2.5x+5>0时，x<2;当-2.5x+5<0时，x>2。由图可知，当x-3>0时，x>3;当X-3<0时，x<3。3.根据下列一次函数的图像，直接写出下列不等式y>0和y<0的解集。 由图可知，当3x+6>0时，即x>-2时y>0;当3x+6<0时，即x<-2时y<0 。由图可知，当-x+2>0时, 即x<2时y>0;当-x+2<0时，即x>2时y<0 。y=-x+2    6、已知一次函数y=kx+b的图像经过点（0,2）和（-3,0），则kx+b<0的解集为（ ）A、x>-3 B、x<-3 C、x>2 D、-30，且一次函数过一、二、三象限，所以选B 理解一元一次不等式与一次函数的关系课后回顾利用一次函数图像求不等式的解集培养数形结合的思想谢谢~