2023年中考数学二轮专项练习：函数(含答案)

这是一份2023年中考数学二轮专项练习：函数(含答案)，共12页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
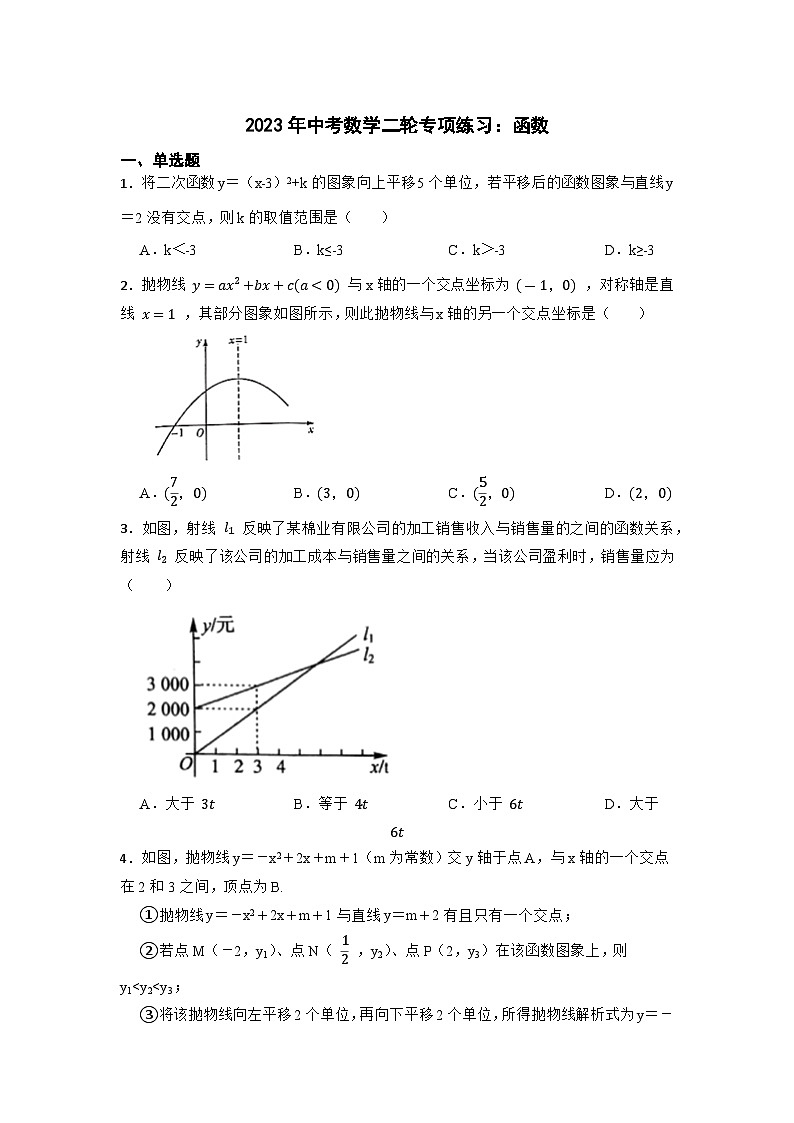
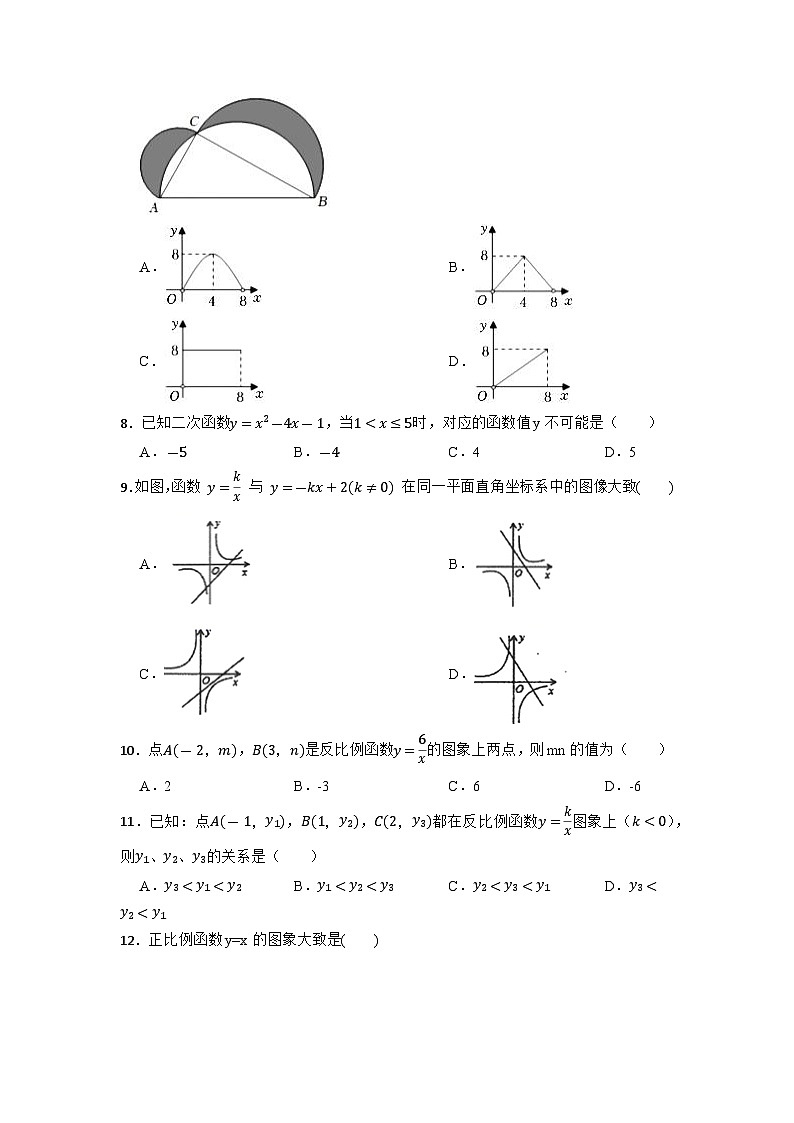
 2023年中考数学二轮专项练习：函数一、单选题1．将二次函数y＝（x﹣3）2+k的图象向上平移5个单位，若平移后的函数图象与直线y＝2没有交点，则k的取值范围是（　　）  A．k＜﹣3 B．k≤﹣3 C．k＞﹣3 D．k≥﹣32．抛物线 与x轴的一个交点坐标为 ，对称轴是直线 ，其部分图象如图所示，则此抛物线与x轴的另一个交点坐标是（　　）  A． B． C． D．3．如图，射线 反映了某棉业有限公司的加工销售收入与销售量的之间的函数关系，射线 反映了该公司的加工成本与销售量之间的关系，当该公司盈利时，销售量应为（　　）  A．大于  B．等于  C．小于  D．大于 4．如图，抛物线y＝－x2＋2x＋m＋1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B.  ①抛物线y＝－x2＋2x＋m＋1与直线y＝m＋2有且只有一个交点；②若点M（－2，y1）、点N（ ，y2）、点P（2，y3）在该函数图象上，则y1<y2<y3；③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝－（x＋1）2＋m；④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为 .其中正确判断有（　　）A．①②③④ B．②③④ C．①③④ D．①③5．在平面直角坐标系中，一次函数的图象可能是（　　）A． B．C． D．6．已知M、N两点关于y轴对称，且点M在反比例函数 的图象上，点N在直线y＝x+4上，设点M的坐标为（a，b），则二次函数y＝﹣abx2+（a+b）x有（　　）   A．最小值为2 B．最大值为2 C．最小值为﹣2 D．最大值为﹣27．如图△ABC中，∠ACB＝90°，AC+BC＝8，分别以AB、AC、BC为半径作半圆，若记图中阴影部分的面积为y，AC为x，则下列y关于x的图象中正确的是（　　）A． B．C． D．8．已知二次函数，当时，对应的函数值y不可能是（　　）A． B． C．4 D．59．如图，函数 与 在同一平面直角坐标系中的图像大致(　　)   A． B．C． D．10．点，是反比例函数的图象上两点，则mn的值为（　　）A．2 B．-3 C．6 D．-611．已知：点，，都在反比例函数图象上（），则、、的关系是（　　）A． B． C． D．12．正比例函数y=x的图象大致是(　　)  A． B．C． D．二、填空题13．已知，，三点都在二次函数的图象上，则，，的大小关系为　         　.14．某地1﹣12月大米的平均价格如下表所示，其中自变量是　     　，因变量是　     　；当自变量等于　     　时，因变量的值　     　最小． 月份  1  2  3  4  5  6  7  8  9  10  11  12  平均价格（元/kg）  3.3  3.4  3.4  3.5  3.4  3.2  3.0  2.9  2.8  2.8  2.9  3.0 15．如图，平行四边形 的顶点 分别在 轴和 轴上，顶点 在反比例函数 的图象上，则平行四边形 的面积是　     　．  16．课间操时，小华，小军，小刚的位置如图．若小华的位置用表示，小军的位置用表示，则小刚的位置用坐标表示为　     　．17．小球从离地面为h（单位：m）的高处自由下落，落到地面所用时间为t（单位：s），经过实验，发现h与 成正比例关系，当 时， ，则当 时，t的值是　     　．  18．已知点P（x0，y0）和直线y＝kx＋b，则点P到直线y＝kx＋b的距离d可用公式 计算.例：求点P（﹣2，1）到直线y＝x＋1的距离.  解：由直线y＝x＋1可知k＝1，b＝1，所以点P（﹣2，1）到直线y＝x＋1的距离为 ＝ ，根据以上材料，写出点P（2，﹣1）到直线y＝3x﹣2的距离为　     　.三、综合题19．为贯彻执行“德、智、体、美、劳”五育并举的教育方针，内江市某中学组织全体学生前往某劳动实践基地开展劳动实践活动.在此次活动中，若每位老师带队30名学生，则还剩7名学生没老师带；若每位老师带队31名学生，就有一位老师少带1名学生.现有甲、乙两型客车，它们的载客量和租金如表所示：
 甲型客车乙型客车载客量（人/辆）3530租金（元/辆）400320学校计划此次劳动实践活动的租金总费用不超过3000元.（1）参加此次劳动实践活动的老师和学生各有多少人？（2）每位老师负责一辆车的组织工作，请问有哪几种租车方案？（3）学校租车总费用最少是多少元？20．如图，平面直角坐标系中， 的顶点都在格点上，已知点 的坐标是 ． （1）点 的坐标是　     　；（2）画出 关于 轴对称的 ，其中点 、 、 的对应点分别为点 、 、 ；（3）直接写出 的面积为　     　．21．在加快“复工复产”的行动中，某通讯运营商的手机上网流量资费标准推出了三种优惠方案：方案 ：按流量计费， 元 ；方案 ： 元流量套餐包月，包含 流量，如果超过 ，超过部分另外计费（见图象），如果用到 时，超过 的流量不再收费；方案 ： 元包月，无限制使用．用 表示每月上网流量（单位： ）， 表示每月的流量费用（单位：元），方案 和方案 对应的 关于 的函数图象如图所示，请解决以下问题：（1）求方案 的函数解析式，并在图中画出其图象；   （2）若小明奶奶每月使用流量在 之间，请通过计算给出经济合理的选择方案．   （3）小明爸爸根据自己平时使用流量的情况，决定采用最经济的方案是 ，则他每月使用流量最可能的范围是　           　．（直接写出答案）   22．已知函数y＝|x|﹣2（1）画出该函数的图象；列表：x…　　　　　　　　…y…　　　　　　　　…描点，连线得到函数图象：（2）写出该函数的两条性质；（3）点P（x1，y1），Q（x2，y2）在该函数的图象上，若x1+x2＝0，求证：y1﹣y2＝0．23．如图在平面直角坐标系 中，一次函数 的图象与反比例函数 的图象交于第二、四象限内的 、 两点，与 轴交于 点，点 的坐标为 ．线段 ， 为 轴上一点，且 ．  （1）求该反比例函数和一次函数的解析式；   （2）求 的面积；   24．如图，直线y=k1x+b与双曲线y=相交于A（1，2）、B（m，-1）两点．（1）求直线和双曲线的函数表达式；     （2）观察图象，请直接写出不等式k1x+b＞的解集；
答案解析部分1．【答案】C2．【答案】B3．【答案】D4．【答案】C5．【答案】B6．【答案】B7．【答案】A8．【答案】D9．【答案】B10．【答案】D11．【答案】C12．【答案】C13．【答案】14．【答案】月份；价格；9、10；2.815．【答案】316．【答案】17．【答案】18．【答案】19．【答案】（1）解：设参加此次劳动实践活动的老师有x人，参加此次劳动实践活动的学生有（30x+7）人，根据题意得：30x+7＝31x﹣1，解得x＝8，∴30x+7＝30×8+7＝247，答：参加此次劳动实践活动的老师有8人，参加此次劳动实践活动的学生有247人；（2）解：师生总数为247+8＝255（人）， ∵每位老师负责一辆车的组织工作，∴一共租8辆车，设租甲型客车m辆，则租乙型客车（8﹣m）辆，根据题意得：，解得3≤m≤5.5，∵m为整数，∴m可取3、4、5，∴一共有3种租车方案：租甲型客车3辆，租乙型客车5辆或租甲型客车4辆，租乙型客车4辆或租甲型客车5辆，租乙型客车3辆；（3）解：设租甲型客车m辆，则租乙型客车（8﹣m）辆，由（2）知：3≤m≤5.5，设学校租车总费用是w元，w＝400m+320（8﹣m）＝80m+2560，∵80＞0，∴w随m的增大而增大，∴m＝3时，w取最小值，最小值为80×3+2560＝2800（元），答：学校租车总费用最少是2800元.20．【答案】（1）（2）解：如图所示，找到点 关于 轴对称的对应点 ，顺次连接 ，则 即为所求； （3）1221．【答案】（1）解：由题意可得，  方案A的函数解析式为y=0.1x，图象如下图所示：（2）解：如图，设直线 的解析式为 ，将 ， 代入   解得 ．将y=20代入y=0.1x，得x=200，即 ，联立 ，解得 ，所以 ， 每月的流量在 之间时选择 方案比较省钱又 ， ，所以选择 方案比较省钱．（3）大于 22．【答案】（1）解：列表： x…01234…y…210012…描点，连线得到函数图象：（2）由图象可知：函数y＝|x|﹣2的图象关于y轴对称； 函数的最小值是 ；当x<0时，y随x的增大而增大；当x>0时，y随x的增大而减小（3）解：∵ ，  ∴ ，∴ ，∵ ，∴ ，∴ ．23．【答案】（1）解：过 作 轴交 轴于 ，   ∴ ， ，∴ ，∴ ，∴ ，将 代入 ，得 ，∴反比例函数的解析式为 ，将 代入 ，得 ，∴ ，将 和 分别代入 ，得 ，解得 ，∴直线解析式： （2）解：在直线 中，令 ，则有 ，解得 ，   ∴ ，即 ，∴ ；同理 ，则 24．【答案】（1）解：∵双曲线y＝经过点A（1，2），∴k2＝2，∴双曲线的解析式为y＝；∵点B（m，−1）在双曲线y＝上，∴m＝−2，∴B点坐标为（−2，−1），把点A（1，2），B（−2，−1）代入y＝k1x＋b，解得，∴直线的解析式为：y＝x＋1；（2）x＞1或-2＜x＜0