2023年中考数学二轮专项练习：函数基础知识(含答案)

这是一份2023年中考数学二轮专项练习：函数基础知识(含答案)，共12页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
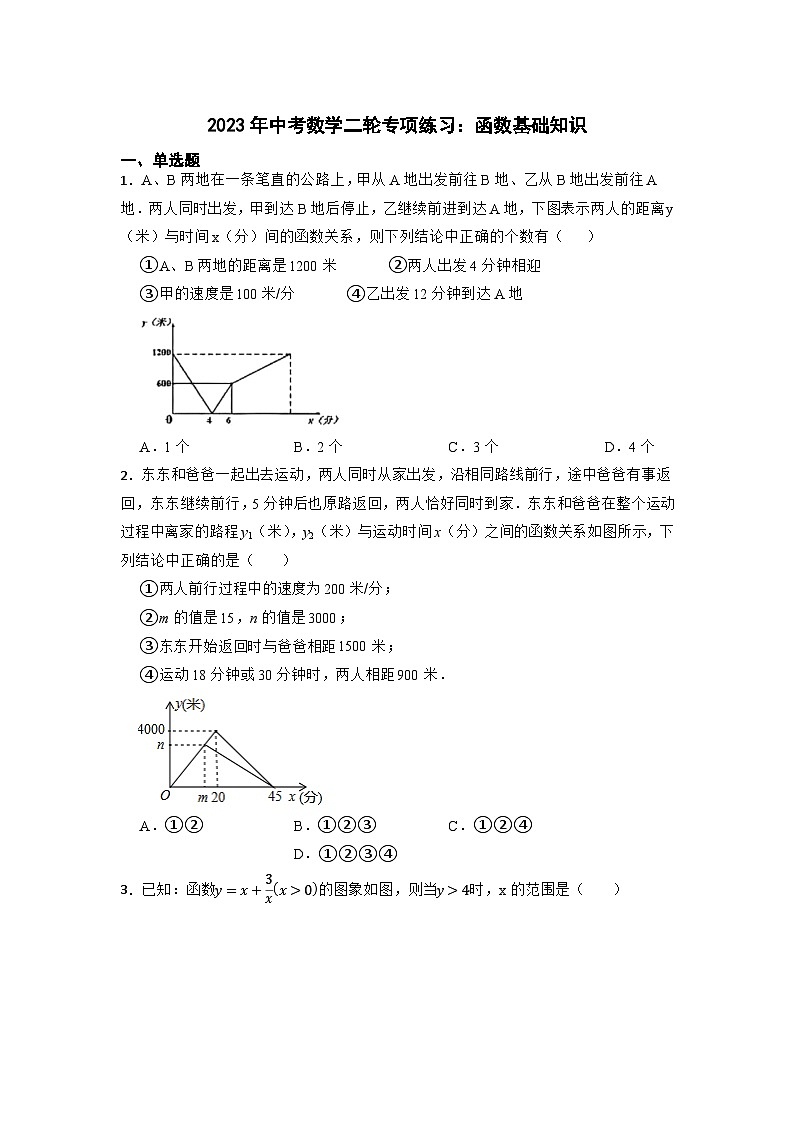
 2023年中考数学二轮专项练习：函数基础知识一、单选题1．A、B两地在一条笔直的公路上，甲从A地出发前往B地、乙从B地出发前往A地．两人同时出发，甲到达B地后停止，乙继续前进到达A地，下图表示两人的距离y（米）与时间x（分）间的函数关系，则下列结论中正确的个数有（　　）①A、B两地的距离是1200米       ②两人出发4分钟相迎③甲的速度是100米/分       ④乙出发12分钟到达A地A．1个 B．2个 C．3个 D．4个2．东东和爸爸一起出去运动，两人同时从家出发，沿相同路线前行，途中爸爸有事返回，东东继续前行，5分钟后也原路返回，两人恰好同时到家．东东和爸爸在整个运动过程中离家的路程y1（米），y2（米）与运动时间x（分）之间的函数关系如图所示，下列结论中正确的是（　　）  ①两人前行过程中的速度为200米/分；②m的值是15，n的值是3000；③东东开始返回时与爸爸相距1500米；④运动18分钟或30分钟时，两人相距900米．A．①② B．①②③ C．①②④ D．①②③④3．已知：函数的图象如图，则当时，x的范围是（　　）
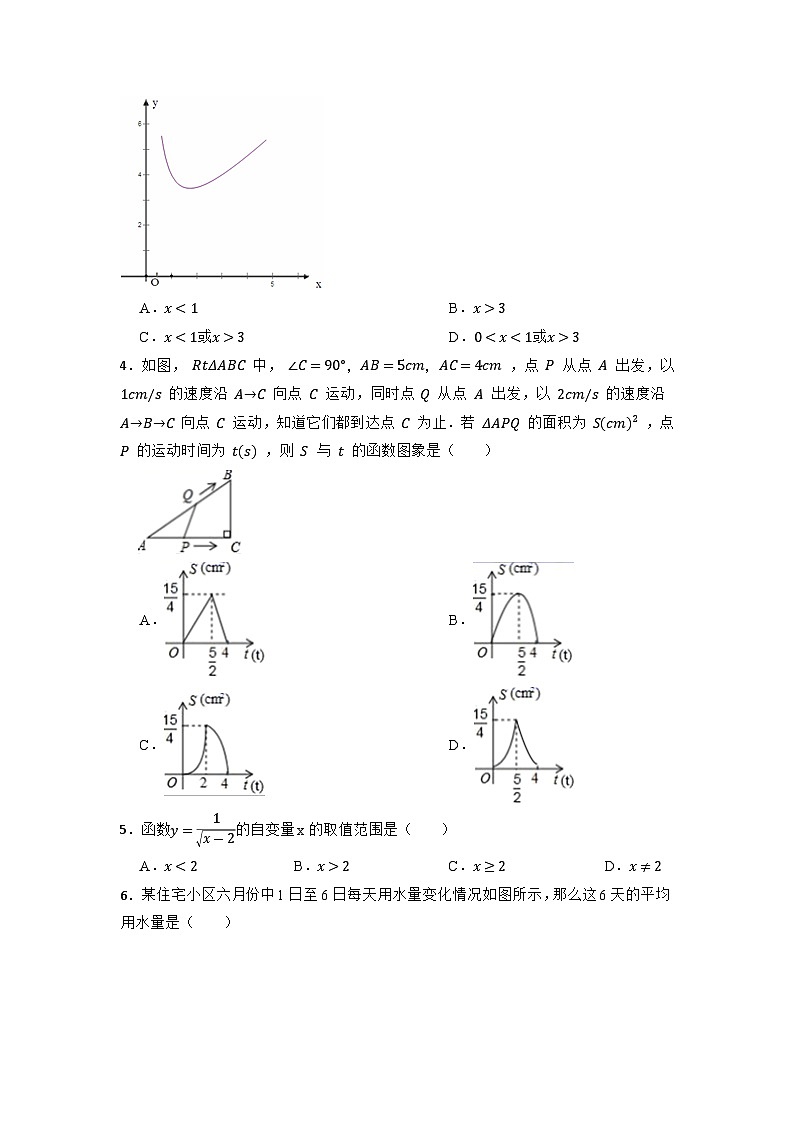
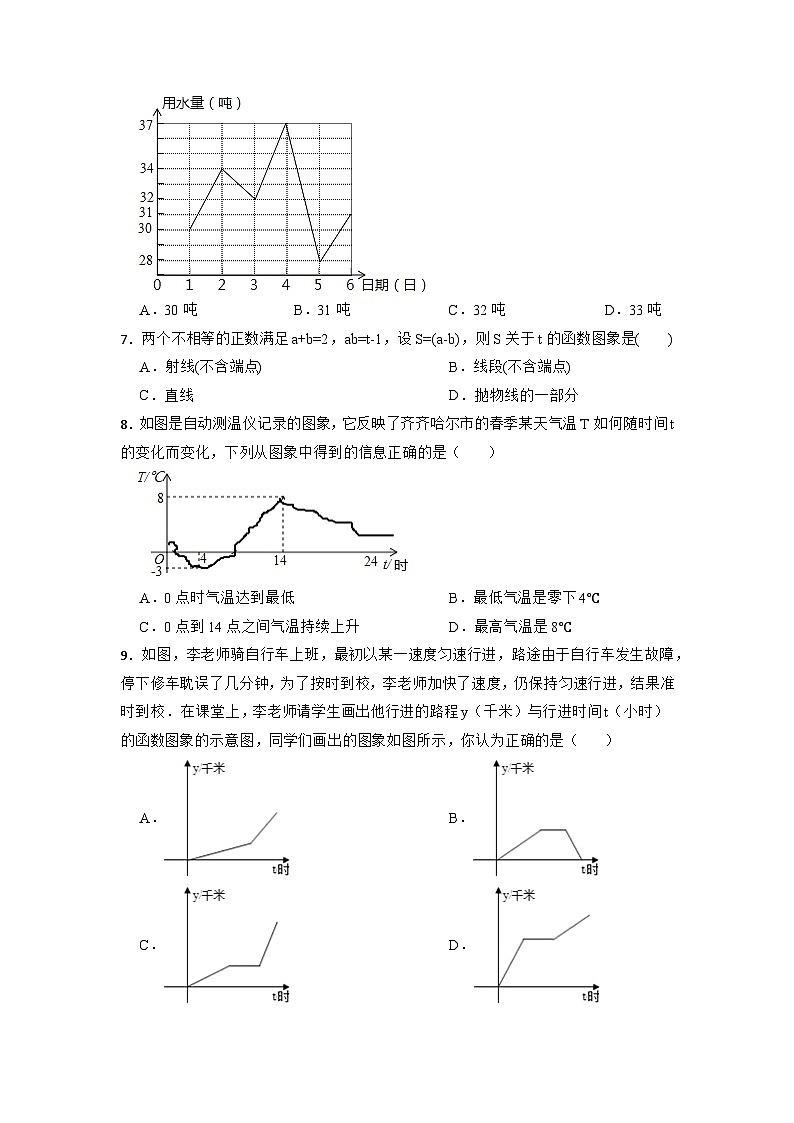
 A． B．C．或 D．或4．如图， 中， ，点 从点 出发，以 的速度沿 向点 运动，同时点 从点 出发，以 的速度沿 向点 运动，知道它们都到达点 为止．若 的面积为 ，点 的运动时间为 ，则 与 的函数图象是（　　） A． B．C． D．5．函数的自变量x的取值范围是（　　）A． B． C． D．6．某住宅小区六月份中1日至6日每天用水量变化情况如图所示，那么这6天的平均用水量是（　　）  A．30吨 B．31吨 C．32吨 D．33吨7．两个不相等的正数满足a+b=2，ab=t-1，设S=(a-b)，则S关于t的函数图象是(　　)A．射线(不含端点) B．线段(不含端点)C．直线 D．抛物线的一部分8．如图是自动测温仪记录的图象，它反映了齐齐哈尔市的春季某天气温T如何随时间t的变化而变化，下列从图象中得到的信息正确的是（　　）A．0点时气温达到最低 B．最低气温是零下4℃C．0点到14点之间气温持续上升 D．最高气温是8℃9．如图，李老师骑自行车上班，最初以某一速度匀速行进，路途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，结果准时到校．在课堂上，李老师请学生画出他行进的路程y（千米）与行进时间t（小时）的函数图象的示意图，同学们画出的图象如图所示，你认为正确的是（　　）A． B．C． D．10．小聪和小明分别从相距30公里的甲、乙两地同时出发相向而行，小聪骑摩托车到达乙地后立即返回甲地，小明骑自行车从乙地直接到达甲地，函数图象y1（km）和y2（km）分别表示小聪离甲地的距离和小明离乙地的距离与已用时间t（h）之间的关系，如图所示．下列说法：①折线段OAB是表示小聪的函数图象y1，线段OC是表示小明的函数图象y2；②小聪去乙地和返回甲地的平均速度相同；③两人在出发80分钟后第一次相遇；④小明骑自行车的平均速度为15km/h，其中不正确的个数为（　　）A．0个 B．1个 C．2个 D．3个11．如图，正△ABC的边长为4，点P为BC边上的任意一点（不与点B、C重合），且∠APD=60°，PD交AB于点D．设BP=x，BD=y，则y关于x的函数图象大致是（　　）  A．A B．B C．C D．D12．小李和小陆从A地出发，骑自行车沿同一条路行驶到B地，他们离出发地的距离S（单位：km）和行驶时间t（单位：h）之间的函数关系的图象如图所示，根据图中的信息，有下列说法：
（1）他们都行驶了20 km；
（2）小陆全程共用了1.5h；
（3）小李和小陆相遇后，小李的速度小于小陆的速度；
（4）小李在途中停留了0.5h．其中正确的有（　　）A．4个 B．3个 C．2个 D．1个二、填空题13．小明和小强进行百米赛跑，小明比小强跑得快，如果两人同时起跑，小明肯定赢，如图所示，现在小明让小强先跑　     　米，直线　     　表示小明的路程与时间的关系，大约　     　秒时，小明追上了小强，小强在这次赛跑中的速度是　     　 .  14．如图，抛物线y1=a（x+2）2+m过原点，与抛物线y2= （x﹣3）2+n交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．下列结论：①两条抛物线的对称轴距离为5；②x=0时，y2=5；③当x＞3时，y1﹣y2＞0；④y轴是线段BC的中垂线．正确结论是　     　（填写正确结论的序号）．  15．在函数y= +x﹣2中，自变量x的取值范围是　             　．  16．函数 的自变量x的取值范围是　     　．  17．将 代入反比例函数 中，所得函数值记为 ，又将 代入原反比例函数中，所得函数值记为 ，再将 代入原反比例函数中，所得函数值记为 ，…，如此继续下去，则 　     　.  18．小明早上步行去车站，然后坐车去学校．如图象中，能近似的刻画小明离学校的距离随时间变化关系的图象是　     　．（填序号）三、综合题19．小凡与小光从学校出发到距学校5千米的图书馆看书，途中小凡从路边超市买了一些学习用品， 如图反映了他们俩人离开学校的路程s(千米)与时间t (分钟) 的关系，请根据图象提供的信息回答问题：  （1）l1和l2中，　     　描述小凡的运动过程；   （2）　     　先到达图书馆，先到了　     　分钟；   （3）当t＝　     　分钟时，小凡与小光在去图书馆的路上相遇；   （4）小凡与小光从学校到图书馆的平均速度各是多少千米/小时(不包括中间停留的时间)   20．下表给出了两个变量x，y的部分对应值x…0.511.523468…y…1264321.510.75…（1）以表中x的值为横坐标，对应的y的值为纵坐标，在给出的平面直角坐标系中描点；（2）选用一个你学过的函数来描述两个变量x，y之间的关系，并确定其函数表达式．21．草莓是云南多地盛产的一种水果，今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量y（千克）与销售单价x（元）符合一次函数关系，如图是y与x 的函数关系图象．（1）求y与x的函数关系式；（2）直接写出自变量x的取值范围．22．已知 与 成正比例，当 时， ，求：  （1） 与 的函数解析式；  （2）当 时，求 的值.  23．某景点试开放期间，团队收费方案如下：不超过30人时，人均收费120元；超过30人且不超过m（30＜m≤100）人时，每增加1人，人均收费降低1元；超过m人时，人均收费都按照m人时的标准．设景点接待有x名游客的某团队，收取总费用为y元．  （1）求y关于x的函数表达式；  （2）景点工作人员发现：当接待某团队人数超过一定数量时，会出现随着人数的增加收取的总费用反而减少这一现象．为了让收取的总费用随着团队中人数的增加而增加，求m的取值范围．  24．已知函数 （ 为常数且 ）中，当 时， ；当 时， .请对该函数及其图像进行如下探究：（1）求该函数的解析式，并直接写出该函数自变量 的取值范围：（2）请在下列直角坐标系中画出该函数的图象： 列表如下：x…-4-3-2-10123456…y… 　 　 　 　 　 　 　 　 　 　 　 　 　…描点连线：（3）请结合所画函数图象，写出函数图象的两条性质（4）请你在上方直角坐标系中画出函数 的图像，结合上述函数的图象，写出不等式 的解集.
答案解析部分1．【答案】C2．【答案】D3．【答案】D4．【答案】C5．【答案】B6．【答案】C7．【答案】B8．【答案】D9．【答案】C10．【答案】B11．【答案】C12．【答案】A13．【答案】10；12；20；3m/s14．【答案】①③④15．【答案】x≥﹣4且x≠016．【答案】x＞﹣217．【答案】218．【答案】④19．【答案】（1）（2）小光；10（3）34（4）∵小凡总用时 ，   ∴小凡的平均速度为： ，小光的平均速度为： ，答：小凡的平均速度为10km/h，小光的平均速度为7.5km/h．20．【答案】（1）解：描点如下 （2）解：观察这些点的排列规律，可用反比例函数描述两个变量x，y之间的关系，设y= ，∵点(2，3)在函数图象上，∴3= ，k=6，∴函数表达式为y= 21．【答案】（1）解：设y与x的函数关系式为y=kx+b，根据题意，得： 解得：  ∴y与x的函数解析式为y=-2x+340（2）解：∵试销期间销售单价不低于成本单价，也不高于每千克40元，且草莓的成本为每千克20元， ∴自变量x的取值范围是20≤x≤4022．【答案】（1）解： 与 成正比例， ，其中 ，  把 ， 代入 得， ，解得： ，（2）解：当 时，  ，解得： 23．【答案】（1）解：y= ，其中（30＜m≤100）（2）解：由（1）可知当0＜x≤30或m＜x＜100，函数值y都是随着x是增加而增加，当30＜x≤m时，y=﹣x2+150x=﹣（x﹣75）2+5625，∵a=﹣1＜0，∴x≤75时，y随着x增加而增加，∴为了让收取的总费用随着团队中人数的增加而增加，∴30＜m≤7524．【答案】（1）解： 已知函数 ，当 时， ；当 时， ∴∴∴该函数解析式为 ；（2）解： 列表如下， x…-4-3-2-10123456…y…\…描点连线，（3）解： ①当 时， 随 的增大而减小； ②当 时， 随 的增大而减小；③当 时， ；④函数图象在第一、二、四象限； （答案不唯一，写出两条即可）；（4）解： 如图： ∵ 与 的交点为 、 ∴结合函数图象可知， 的解集为 或 .