2023年中考数学二轮专题训练——几何探究压轴题(含答案)

这是一份2023年中考数学二轮专题训练——几何探究压轴题(含答案)，共12页。试卷主要包含了已知，已知，为等边三角形，点在边上，综合与实践，问题提出，已知是等腰直角三角形，，，课本再现，四边形中，，M为上一点，连、等内容，欢迎下载使用。
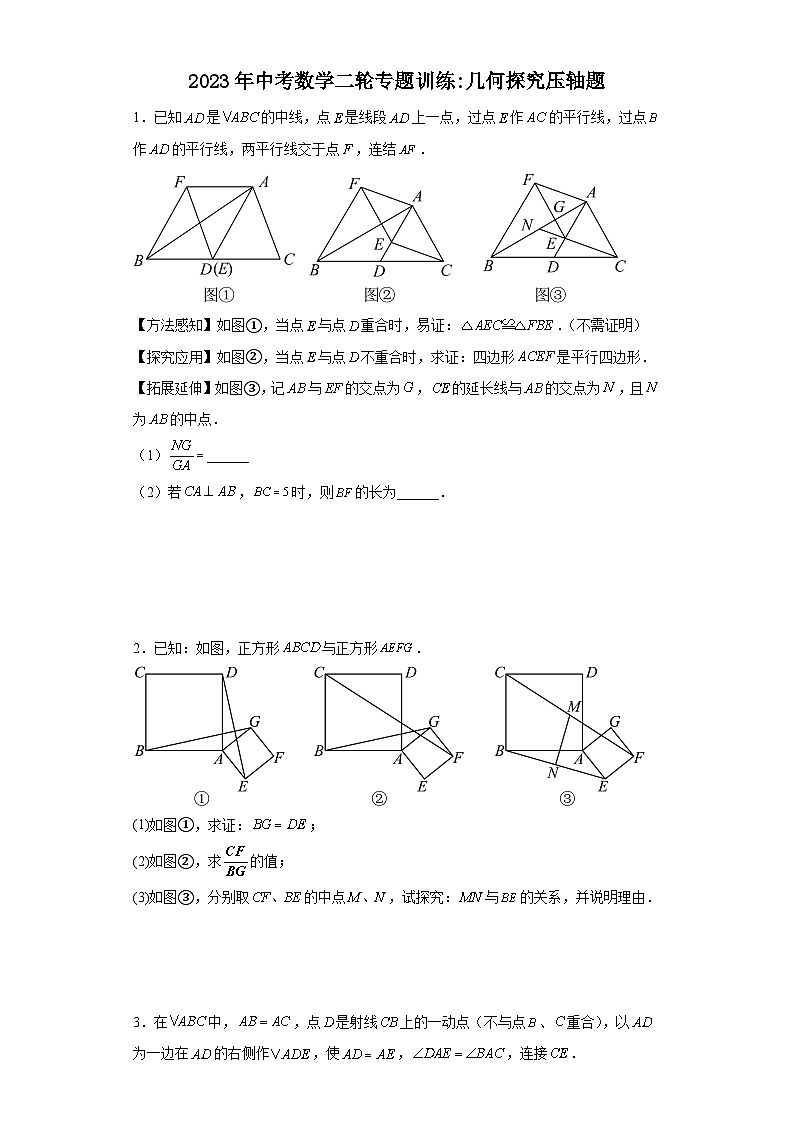
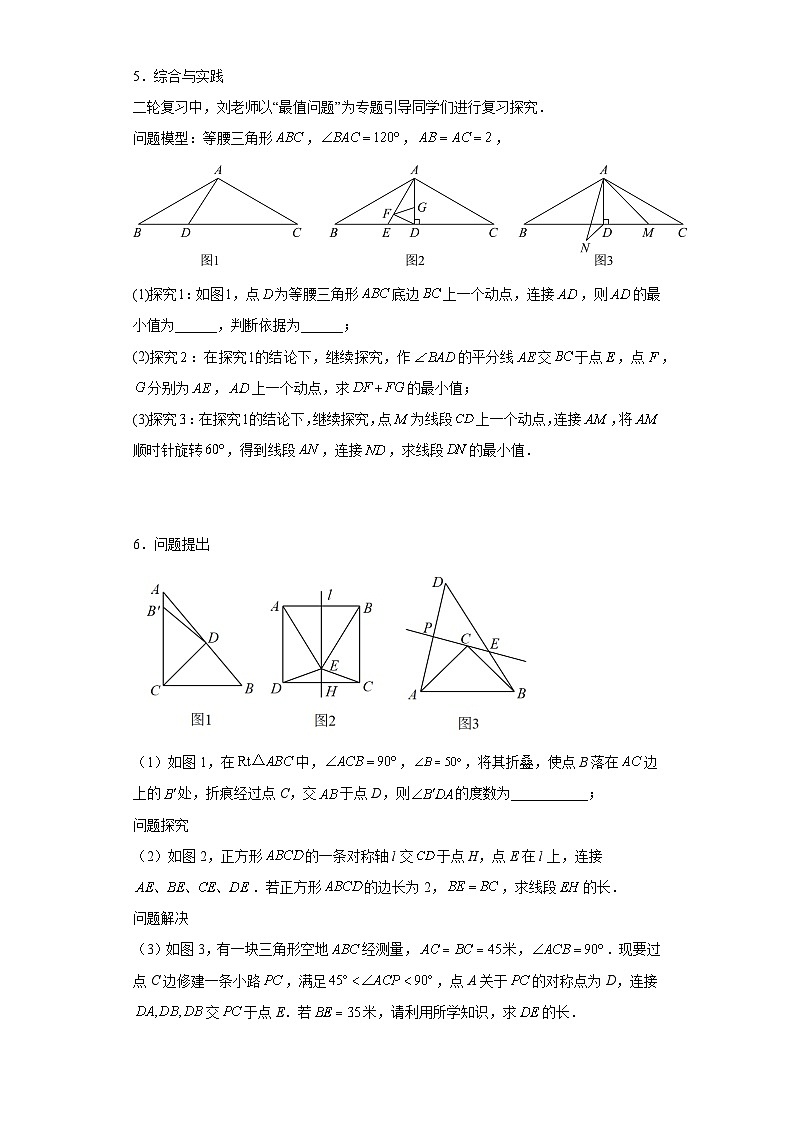
2023年中考数学二轮专题训练:几何探究压轴题1．已知是的中线，点是线段上一点，过点作的平行线，过点作的平行线，两平行线交于点，连结．             【方法感知】如图①，当点与点重合时，易证：．（不需证明）【探究应用】如图②，当点与点不重合时，求证：四边形是平行四边形．【拓展延伸】如图③，记与的交点为，的延长线与的交点为，且为的中点．（1）______（2）若，时，则的长为______．    2．已知：如图，正方形与正方形．(1)如图①，求证：；(2)如图②，求的值；(3)如图③，分别取的中点，试探究：与的关系，并说明理由．   3．在中，，点是射线上的一动点（不与点、重合），以为一边在的右侧作，使，，连接．(1)如图1，当点在线段上，且时，那么________度；(2)设，．①如图2，当点D在线段上，时，请你探究与之间的数量关系，并证明你的结论；②如图3，当点D在线段的延长线上，时，请将图3补充完整；写出此时与之间的数量关系，并说明理由．   4．已知，为等边三角形，点在边上．【基本图形】如图1，以为一边作等边三角形，连结．可得（不需证明）．【迁移运用】如图2，点是边上一点，以为一边作等边三角．求证：．【类比探究】如图3，点是边的延长线上一点，以为一边作等边三角．试探究线段，，三条线段之间存在怎样的数量关系，请写出你的结论并说明理由．    5．综合与实践二轮复习中，刘老师以“最值问题”为专题引导同学们进行复习探究．问题模型：等腰三角形，，，(1)探究：如图，点为等腰三角形底边上一个动点，连接，则的最小值为______，判断依据为______；(2)探究：在探究的结论下，继续探究，作的平分线交于点，点，分别为，上一个动点，求的最小值；(3)探究：在探究的结论下，继续探究，点为线段上一个动点，连接，将顺时针旋转，得到线段，连接，求线段的最小值．  6．问题提出（1）如图1，在中，，，将其折叠，使点B落在边上的处，折痕经过点C，交于点D，则的度数为___________；问题探究（2）如图2，正方形的一条对称轴l交于点H，点E在l上，连接．若正方形的边长为2，，求线段的长．问题解决（3）如图3，有一块三角形空地经测量，米，．现要过点C边修建一条小路，满足，点A关于的对称点为D，连接交于点E．若米，请利用所学知识，求的长． 7．已知是等腰直角三角形，，(1)如图1，是等腰直角三角形，点D在的延长线上，，连接，求证：；(2)如图2，点F是斜边上动点，点G是延长线上动点，总有，探究的数量关系，并说明理由；(3)如图3，点H是一点，连接FH，若，，，直接写出的面积为____________（用m，n表示）．   8．课本再现如图1，在等边中，为边上一点，为上一点，且，连接与相交于点．(1)与的数量关系是______，与构成的锐角夹角的度数是______．深入探究(2)将图1中的延长至点，使，连接，，如图2所示．求证：平分．（第一问的结论，本问可直接使用）迁移应用(3)如图3，在等腰中，，，分别是边，上的点，与相交于点．若，且，求的值．  9．四边形中，，M为上一点，连、． (1)平分，，①如图1，求证：；②如图2，若平分，交于F，交于N，， ；(2)在（1）的条件下求的值；(3)如图3，当,时，试探究与的数量关系，证明你的结论．   10．综合与实践问题情境：数学活动课上，老师出示了一个问题：如图①，在中，，垂足为E，F为的中点，连接，，试猜想与的数量关系，并加以证明．(1)独立思考：请解答老师提出的问题；(2)实践探究：希望小组受此问题的启发，将沿着（F为的中点）所在直线折叠，如图②，点C的对应点为，连接并延长交于点G，请判断与的数量关系，并加以证明．(3)问题解决：智慧小组突发奇想，将沿过点B的直线折叠，如图③，点A的对应点为，使于点H，折痕交于点M，连接，交于点N．该小组提出一个问题：若此的面积为20，边长，，求图中阴影部分（四边形）的面积．请你思考此问题，直接写出结果．    11．问题提出：已知矩形，点为上的一点，，交于点．将绕点顺时针旋转得到，则与有怎样的数量关系．【问题探究】探究一：如图，已知正方形，点为上的一点，，交于点．（1）如图1，直接写出的值 ；（2）将绕点顺时针旋转到如图所示的位置，连接、，猜想与的数量关系，并证明你的结论；探究二：如图，已知矩形，点为上的一点，，交于点．如图3，若四边形为矩形，，将绕点顺时针旋转得到、的对应点分别为、点，连接、，则的值是否随着的变化而变化．若变化，请说明变化情况；若不变，请求出的值．【一般规律】如图3，若四边形为矩形，，其它条件都不变，将绕点顺时针旋转得到，连接，，请直接写出与的数量关系．    12．定义：有一个角是直角的平行四边形叫做矩形．(1)根据定义判矩形已知：如图1，在平行四边形中，是它的两条对角线，．求证：平行四边形是矩形．(2)动手操作有发现如图2，在矩形中，是的中点，将沿折叠后得到，点在矩形内部，延长交于点．猜想线段与有何数量关系?并证明你的结论．(3)类比探究到一般如图3，将(2)中的矩形改为平行四边形，其它条件不变，(2)中的结论是否仍然成立，请说明理由．(4)解决问题巧应用如图4，保持(2)中的条件不变，若点是的中点，且，请直接写出矩形的面积．  13．在中，，，点P是平面内不与点A，C重合的任意一点，连接，将线段绕点P逆时针旋转α得到线段，连接，，.(1)观察猜想如图①，当时，的值是_______，直线与直线相交所成的较小角的度数是________．(2)类比探究如图②，当时，请写出的值及直线与直线相交所成的较小角的度数，并就图②的情形说明理由．   14．（1）（问题背景）如图1，在等边中，点M是边上一点，连接，以为边作等边（A，M，N按逆时针方向排列），连接，求证：（2）（变式探究）如图2，已知，指出图中的另外一对相似三角形并进行证明；（3）（拓展应用）如图3，在和中，，，点D在边上，求的值．        15．（1）【操作发现】如图1，四边形都是矩形，，，小明将矩形绕点C顺时针转，如图2所示．①若的值不变，请求出的值，若变化，请说明理由．②在旋转过程中，当点B、E、F在同一条直线上时，画出图形并求出的长度．（2）【类比探究】如图3，中， ， ，G为中点，D为平面内一个动点，且，将线段绕点D逆时针旋转得到，则四边形面积的最大值为 ．（直接写出结果）  16．如图1，在矩形中，，动点P从B出发，以每秒1个单位的速度，沿射线方向移动，作关于直线的对称，设点P的运动时间为．(1)若．①如图2，当点落在上时，求证：，②是否存在异于图2的时刻，使得是直角三角形？若存在，请直接写出所有符合题意的t的值？若不存在，请说明理由．(2)当P点不与C点重合时，若直线与直线相交于点M，且当时存在某一时刻有结论成立，试探究：对于的任意时刻，结论“”是否总是成立？请说明理由．  17．在正方形中，是边上一点（点不与点、重合），连结．感知：如图①，过点作交于点．求证．探究：如图②，取的中点，过点作交于点，交于点．（1）求证：．（2）连结，若，求的长．应用如图③，取的中点，连结．过点作交于点，连结、．若，求四边形的面积．   18．点在四边形的对角线上，直角三角板绕直角顶点旋转，其边、分别交、边于点、．操作发现：如图①，若四边形是正方形，当时，可知四边形是正方形，显然．当与不垂直时，判断确定、之间的数量关系；______．（直接写出结论即可）类比探究：如图②，若四边形是矩形，试说明．拓展应用：如图③，改变四边形、的形状，其他条件不变，且满足，，，时，求的值．
参考答案：1．【拓展延伸】（1）；（2）2．(2)(3)， 3．(1)90(2)①，证明见解析；②，5．(1)；点到直线的距离垂线段最短(2)(3) 6．（1）；（2）；（3）米7．(2)(3) 8．(1)；60°(3)3 9．(1) (2)(3) 10．(1)，(2)，(3) 11．[问题探究]探究一：(1)；(2)，探究二：．[一般规律]12．(2)，(3)成立，(4) 13．(1)1，；(2)，， 14．（2）（3）；15．（1）①不变，；②或；（2）2416．(1)②存在，的值为2或6或(2)对于的任意时刻，结论“”总是成立， 17．（（2）2  应用：918．操作发现：；类比探究：拓展应用：