




必刷卷03——【高考三轮冲刺】2023年高考数学考前20天冲刺必刷卷(新高考地区专用)(原卷版+解析版)
展开绝密★启用前
2023年高考数学考前信息必刷卷03
新高考地区专用
预计新高考地区考试题型仍与2022年试卷结构相同,为8(单选题)+4(多选题)+4(填空题)+6(解答题),其中结构不良型试题是新高考地区新增加的题型,主要涉及解三角形与数列两大模块,以解答题的方式进行考查。
2022年新高考Ⅰ卷并未考查结构不良试题,本卷在第17题预测考查四边形面积问题。
应特别注意以给定定义为背景的试题,此类试题要特别注意给定的定义,根据定义找到规律,如本卷第16题,解答本题中函数迭代问题,要结合题设找到迭代规律,即可求出函数表达式,能有效考查学生发现问题、分析问题和解决问题的能力;另外本卷第22题以大热点世界杯为背景,试题包含的信息量大,学生在解题时会出现从长题中提出信息的难度,重点考查了学生提取有效条件,分析问题,并解决问题的能力,本题难度较大。
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2023·全国·模拟预测)设是虚数单位,复数,则的虚部为( )
A. B. C. D.3
【答案】D
【详解】由,
得,
所以,所以的虚部为3.
故选:D.
2.(2023春·黑龙江哈尔滨·高三哈尔滨德强学校校考开学考试)设全集,,,则如图所示的阴影部分所表示的集合是( )
A. B.
C. D.
【答案】C
【详解】由题意得图中阴影部分表示的集合是.∵,∴.又因为,∴.
故选:C.
3.(2023·江苏·高二专题练习)用红、黄、蓝3种颜色给如图所示的6个相连的圆涂色,若每种颜色只能涂2个圆,且相邻2个圆所涂颜色不能相同,则不同的涂法种数为( )
A.24 B.30 C.36 D.42
【答案】B
【详解】分2类(先涂前3个圆,再涂后3个圆.):第1类,前3个圆用3种颜色,后3个圆也用3种颜色,有种涂法;第2类,前3个圆用2种颜色,后3个圆也用2种颜色,有种涂法.综上,不同的涂法和数为.
故选:B.
4.(2023秋·浙江杭州·高二杭州市长河高级中学校考期末)如图所示,在四棱柱中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为,则的长为( )
A. B.2 C. D.
【答案】D
【详解】解:记,,,
由题意可知,,
所以,
,
所以,即的长为,
故选:D.
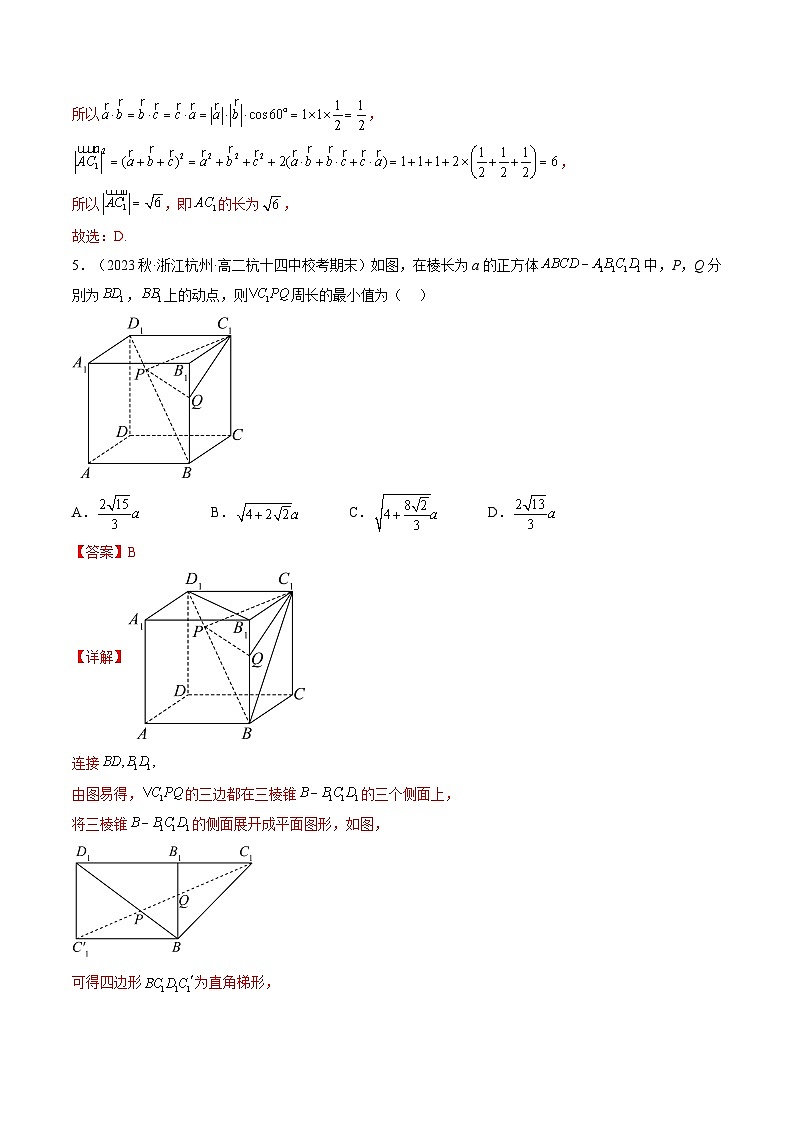
5.(2023秋·浙江杭州·高二杭十四中校考期末)如图,在棱长为a的正方体中,P,Q分別为,上的动点,则周长的最小值为( )
A. B. C. D.
【答案】B
【详解】
连接
由图易得,的三边都在三棱锥的三个侧面上,
将三棱锥的侧面展开成平面图形,如图,
可得四边形为直角梯形,
当四点共线时,的周长最小,
最小值为,
故选:B.
6.(2023·全国·模拟预测)已知双曲线的上、下焦点分别为,,过的直线交双曲线上支于A,B两点,且满足,,则双曲线的离心率为( )
A. B. C. D.
【答案】D
【详解】设,,
则,.
在中,由余弦定理得,
即.
在中,由余弦定理得,
化简得,因为,
所以,
所以,
所以,
∴双曲线的离心率,
故选:D.
7.(2023·全国·高三专题练习)已知,,,则下列判断正确的是( )
A. B. C. D.
【答案】D
【详解】(1)比较a,b的大小:因为,所以,所以.
(2)比较b,c的大小:令,则.
当时,;当时,,
所以当时,,即,所以,即.
(3)比较a,c大小:
因为,所以,即,所以,即.
综上,.
故选:D.
8.(2023秋·浙江金华·高二统考期末)已知数列是各项为正数的等比数列,公比为q,在之间插入1个数,使这3个数成等差数列,记公差为,在之间插入2个数,使这4个数成等差数列,公差为,在之间插入n个数,使这个数成等差数列,公差为,则( )
A.当时,数列单调递减 B.当时,数列单调递增
C.当时,数列单调递减 D.当时,数列单调递增
【答案】D
【详解】数列是各项为正数的等比数列,则公比为,
由题意,得,
时,,有,,数列单调递增,A选项错误;
时,,,若数列单调递增,则, 即,由,需要,故B选项错误;
时,,解得,
时,,由,若数列单调递减,则, 即,而 不能满足恒成立,C选项错误;
时,,解得或,由AB选项的解析可知,数列单调递增,D选项正确.
故选:D
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.(2023·辽宁·辽宁实验中学校考模拟预测)随着我国碳减排行动的逐步推进,我国新能源汽车市场快速发展,新能源汽车产销量大幅上升,2017-2021年全国新能源汽车保有量y(单位:万辆)统计数据如下表所示:
年份
2017年
2018年
2019年
2020年
2021年
年份代码x
1
2
3
4
5
保有量y/万辆
153.4
260.8
380.2
492
784
由表格中数据可知y关于x的经验回归方程为,则( )
A.
B.预测2023年底我国新能源汽车保有量高于1000万辆
C.2017-2021年全国新能源汽车保有量呈增长趋势
D.2021年新能源汽车保有量的残差(观测值与预测值之差)为71.44
【答案】BCD
【详解】由题得,,代入可得,A项错误;
2023年的年份代码为7,代入得,高于1000万辆,B项正确;
2017-2021年全国新能源汽车保有量呈增长趋势,C项显然正确;
将x=5,代入得,相应的残差为784-712.56=71.44,D项正确,
故选:BCD.
10.(2023秋·河北邢台·高三邢台市第二中学校考期末)如图所示,正方体的棱长为1,线段上有两个动点,,且,则下列说法中正确的是( )
A.存在点,,使得
B.异面直线与所成的角为60°
C.三棱锥的体积为
D.点到平面的距离为
【答案】BCD
【详解】连接.
A选项,平面,平面,,
所以与是异面直线,所以A选项错误.
B选项,,所以异面直线与所成的角为,
由于三角形是等边三角形,所以,B选项正确.
C选项,设,根据正方体的性质可知,
由于平面,所以平面,
所以到平面的距离为.
,C选项正确.
D选项,设点到平面的距离为,
,
,
解得,D选项正确.
故选:BCD
11.(2023·吉林·通化市第一中学校校联考模拟预测)已知函数,则( )
A.若函数的图象关于直线对称,则的值可能为3
B.若关于x的方程在上恰有四个实根,则的取值范围为
C.若函数的图象向右平移个单位长度,再向下平移B个单位长度,得到的函数为奇函数,则的最小值是1
D.若函数在区间上单调,则
【答案】BC
【详解】对于A,因为函数的图象关于直线对称,所以,则,因为,则的值不可能为3,故A错误;
对于B,当时,,若在上恰有四个实根,则,解得,故B正确;
对于C,由已知得,因为函数为奇函数,所以,即,因为,所以的最小值是1,故C正确;
对于D,当时,,因为,
所以,所以函数在区间上不单调,故D错误.
故选:BC.
12.(2023·山西忻州·统考模拟预测)已知,分别是定义在R上的函数,的导函数,,,且是奇函数,则( )
A.的图象关于直线对称 B.的图象关于点对称
C. D.
【答案】ABC
【详解】因为,所以(a为常数),
所以.因为,
所以.
令,得,解得,
所以,则的图象关于直线对称,故选项正确.
因为,且,所以.所以,即是偶函数.因为是奇函数,所以的图象关于点对称,所以的图象关于点对称,因为是偶函数,所以的图象关于点对称,则选项正确.
因为是奇函数,所以,所以,
所以,则是周期为4的函数.
因为,所以,所以,,则.因为是奇函数,
所以,所以,
则选项正确.
因为,所以,所以,,,
,所以,所以,
则选项错误.
故选:.
三、填空题:本题共4小题,每小题5分,共20分.
13.(2023·上海黄浦·统考一模)某个品种的小麦麦穗长度(单位:cm)的样本数据如下:10.2、9.7、10.8、9.1、8.9、8.6、9.8、9.6、9.9、11.2、10.6、11.7,则这组数据的第80百分位数为______.
【答案】10.8
【详解】数据从小到大排序为: 8.6、8.9、9.1、9.6、9.7、9.8、9.9、10.2、10.6、10.8、11.2、11.7,共有12个,
所以,
所以这组数据的第80百分位数是第10个数即:10.8.
故答案为:10.8
14.(2023·陕西咸阳·陕西咸阳中学校考模拟预测)函数的值域是___________.
【答案】
【详解】因为
又因为,
所以当时,取得最小值 -1 ,
当时,取得最大值 2 , 故的值域是.
故答案为:
15.(2023·内蒙古呼和浩特·统考一模)抛物线的焦点与双曲线的右焦点的连线交于第一象限的点M,若在点M处的切线平行于的一条渐近线,则__________.
【答案】##
【详解】抛物线的焦点的坐标为,且;
双曲线的右焦点的坐标为,渐近线方程为,
由题意可知,在点M处的切线平行的渐近线应为,
设,则,得,
又点共线,即点共线,
所以,解得,所以.
故答案为:.
16.(2023·广东湛江·统考一模)已知函数,记为函数的2次迭代函数,为函数的3次迭代函数,…,依次类推,为函数的n次迭代函数,则______;除以17的余数是______.
【答案】 0
【详解】由题意,,
所以
又为正整数,
所以除以17的余数为0,
故答案为:
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)
(2023·江苏南通·校联考模拟预测)如图,在平面四边形ABCD中,,,,.
(1)若,求;
(2)记 与 的面积分别记为和,求的最大值.
【答案】(1)
(2)
【详解】(1)∵,∴,
,,
,,
∴
;
(2)设,,∴,
∴,∴,①
,
当且仅当,时取最大值 ;
综上, , 的最大值是 .
18.(12分)
(2023·山东临沂·统考一模)已知数列为等比数列,是与的等差中项,为的前项和.
(1)求的通项公式及;
(2)集合A为正整数集的某一子集,对于正整数,若存在正整数,使得,则,否则.记数列满足,求的前20项和.
【答案】(1)
(2)
【详解】(1)设的公比为是与的等差中项,
,,
∴,.
(2)由题意知,,
又,
,即,
故.
又,
.
19.(12分)
(2023·湖南邵阳·统考二模)如图所示,在四棱锥中,底面是等腰梯形,,.平面平面,为的中点,,,E,F,G分别为,,的中点.
(1)求证:平面平面;
(2)求平面与平面所成锐二面角的正切值.
【答案】(1)证明见解析
(2)
【详解】(1)如图所示,取AO的中点H,连接HD,HP,
在等腰梯形中,,,,.
∵O为AB的中点,即有四边形是平行四边形,
∴,.
∴为正三角形,∴,.
在中,,,
∴为边长为2的正三角形,∴,.
∴,又F为FD的中点,∴.
∵,,,平面,
∴平面,即平面.∵平面,∴.
而G为PC中点,则,又∵,平面,∴平面.
∵平面PCD,∴平面平面.
(2)∵,平面平面,平面平面,平面,
∴平面,
∴由(1)知,PH,HD,AB两两垂直,
以H为坐标原点,HD,HB,HP所在直线分别为x轴,y轴,z轴建立如图所示空间直角坐标系,
则,,,,
于是,,.
设平面的法向量为,
则即取,则,
设平面与平面所成锐二面角为,
∵为平面的一个法向量,
∴.
∴,.
∴平面与平面所成锐二面角的正切值为.
20.(12分)
(2023·宁夏银川·银川二中校考模拟预测)已知椭圆C:的离心率为,点在椭圆C上.
(1)求椭圆C的标准方程;
(2)过点的直线l交椭圆C于P,Q两点,O为坐标原点,求△OPQ面积的最大值.
【答案】(1)
(2)
【详解】(1)由题意可得,
解得,
故椭圆C的标准方程为.
(2)设直线l的方程为,,,
联立,
整理得,
则,即,
解得,,.
故△OPQ的面积.
设,
因为,所以,
所以,
因为,所以,
当且仅当,即时,等号成立,
则,即△OPQ面积的最大值为.
21.(12分)
(2023·新疆阿勒泰·统考一模)已知函数,其中.
(1)求函数的单调区间;
(2)若函数在上存在零点,求实数的取值范围.
【答案】(1)单调递减区间为,单调递增区间为;
(2)
【详解】(1)由已知,,
有,令,解得
由,可知当变化时,的变化情况如下表:
0
-
0
+
递减
极小值
递增
所以函数的单调递减区间为,单调递增区间为;
(2)令,则存在,
使得
两边同时除以得
即
令
由已知,即,
则函数在上单调递增,
故,即
22.(12分)
(2023·浙江·模拟预测)2022年卡塔尔世界杯决赛圈共有32队参加,其中欧洲球队有13支,分别是德国、丹麦、法国、西班牙、英格兰、克罗地亚、比利时、荷兰、塞尔维亚、瑞士、葡萄牙、波兰、威尔士.世界杯决赛圈赛程分为小组赛和淘汰赛,当进入淘汰赛阶段时,比赛必须要分出胜负.淘汰赛规则如下:在比赛常规时间90分钟内分出胜负,比赛结束,若比分相同,则进入30分钟的加时赛.在加时赛分出胜负,比赛结束,若加时赛比分依然相同,就要通过点球大战来分出最后的胜负.点球大战分为2个阶段.第一阶段:前5轮双方各派5名球员,依次踢点球,以5轮的总进球数作为标准(非必要无需踢满5轮),前5轮合计踢进点球数更多的球队获得比赛的胜利.第二阶段:如果前5轮还是平局,进入“突然死亡”阶段,双方依次轮流踢点球,如果在该阶段一轮里,双方都进球或者双方都不进球,则继续下一轮,直到某一轮里,一方罚进点球,另一方没罚进,比赛结束,罚进点球的一方获得最终的胜利.
下表是2022年卡塔尔世界杯淘汰赛阶段的比赛结果:
淘汰赛
比赛结果
淘汰赛
比赛结果
1/8决赛
荷兰美国
1/4决赛
克罗地亚巴西
阿根廷澳大利亚
荷兰阿根廷
法国波兰
摩洛哥葡萄牙
英格兰塞内加尔
英格兰法国
日本克罗地亚
半决赛
阿根廷克罗地亚
巴西韩国
法国摩洛哥
摩洛哥西班牙
季军赛
克罗地亚摩洛哥
葡萄牙瑞士
决赛
阿根廷法国
注:“阿根廷法国”表示阿根廷与法国在常规比赛及加时赛的比分为,在点球大战中阿根廷战胜法国.
(1)请根据上表估计在世界杯淘汰赛阶段通过点球大战分出胜负的概率.
(2)根据题意填写下面的列联表,并通过计算判断是否能在犯错的概率不超过0.01的前提下认为“32支决赛圈球队闯入8强”与是否为欧洲球队有关.
欧洲球队
其他球队
合计
闯入8强
未闯入8强
合计
(3)若甲、乙两队在淘汰赛相遇,经过120分钟比赛未分出胜负,双方进入点球大战.已知甲队球员每轮踢进点球的概率为p,乙队球员每轮踢进点球的概率为,求在点球大战中,两队前2轮比分为的条件下,甲队在第一阶段获得比赛胜利的概率(用p表示).
参考公式:
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
【答案】(1)
(2)分布列见解析,不能
(3)
【详解】(1)由题意知卡塔尔世界杯淘汰赛共有16场比赛,其中有5场比赛通过点球大战决出胜负,
所以估计在世界杯淘汰赛阶段通过点球大战分出胜负的概率;
(2)下面为列联表:
欧洲球队
其他球队
合计
进入8强
5
3
8
未进入8强
8
16
24
合计
13
19
32
零假设支决赛圈球队闯入8强与是否为欧洲球队无关.
.
根据小概率值的独立性检验,没有充分证据推断不成立,
即不能在犯错的概率不超过0.01的前提下认为“决赛圈球队闯入8强”与是否为欧洲球队有关.
(3)根据实际比赛进程,假定点球大战中由甲队先踢.两队前2轮比分为的条件下,甲在第一阶段获得比赛胜利,则后3轮有5种可能的比分,.
当后3轮比分为时,甲乙两队均需踢满5轮,.
当后3轮比分为时,有如下3种情况:
3
4
5
3
4
5
3
4
5
甲
√
√
甲
√
×
√
甲
×
√
√
乙
×
×
乙
×
×
乙
×
×
则.
当后3轮比分为时,有如下6种情况:
3
4
5
3
4
5
3
4
5
甲
√
√
×
甲
√
√
×
甲
√
×
√
乙
√
×
×
乙
×
√
×
乙
√
×
×
3
4
5
3
4
5
3
4
5
甲
√
×
√
甲
×
√
√
甲
×
√
√
乙
×
√
×
乙
√
×
×
乙
×
√
×
则.
当后3轮比分为时,有如下2种情况:
3
4
5
3
4
5
甲
√
√
√
甲
√
√
√
乙
√
×
乙
×
√
则
当后3轮比分为时,有如下1种情况:
3
4
5
甲
√
√
√
乙
√
√
×
则.
综上,在点球大战中两队前2轮比分为的条件下,甲在第一阶段获得比赛胜利的概率
必刷卷03——【高考三轮冲刺】2023年高考数学考前20天冲刺必刷卷(江苏专用)(原卷版+解析版): 这是一份必刷卷03——【高考三轮冲刺】2023年高考数学考前20天冲刺必刷卷(江苏专用)(原卷版+解析版),文件包含必刷卷03高考三轮冲刺2023年高考数学考前20天冲刺必刷卷江苏专用解析版docx、必刷卷03高考三轮冲刺2023年高考数学考前20天冲刺必刷卷江苏专用原卷版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
必刷卷04——【高考三轮冲刺】2023年高考数学考前20天冲刺必刷卷(新高考地区专用)(原卷版+解析版): 这是一份必刷卷04——【高考三轮冲刺】2023年高考数学考前20天冲刺必刷卷(新高考地区专用)(原卷版+解析版),文件包含必刷卷04高考三轮冲刺2023年高考数学考前20天冲刺必刷卷新高考地区专用解析版docx、必刷卷04高考三轮冲刺2023年高考数学考前20天冲刺必刷卷新高考地区专用原卷版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
必刷卷01——【高考三轮冲刺】2023年高考数学考前20天冲刺必刷卷(新高考地区专用)(原卷版+解析版): 这是一份必刷卷01——【高考三轮冲刺】2023年高考数学考前20天冲刺必刷卷(新高考地区专用)(原卷版+解析版),文件包含必刷卷01高考三轮冲刺2023年高考数学考前20天冲刺必刷卷新高考地区专用解析版docx、必刷卷01高考三轮冲刺2023年高考数学考前20天冲刺必刷卷新高考地区专用原卷版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。












