2023年湖北省十堰市郧西县二模数学试题（含答案）

这是一份2023年湖北省十堰市郧西县二模数学试题（含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
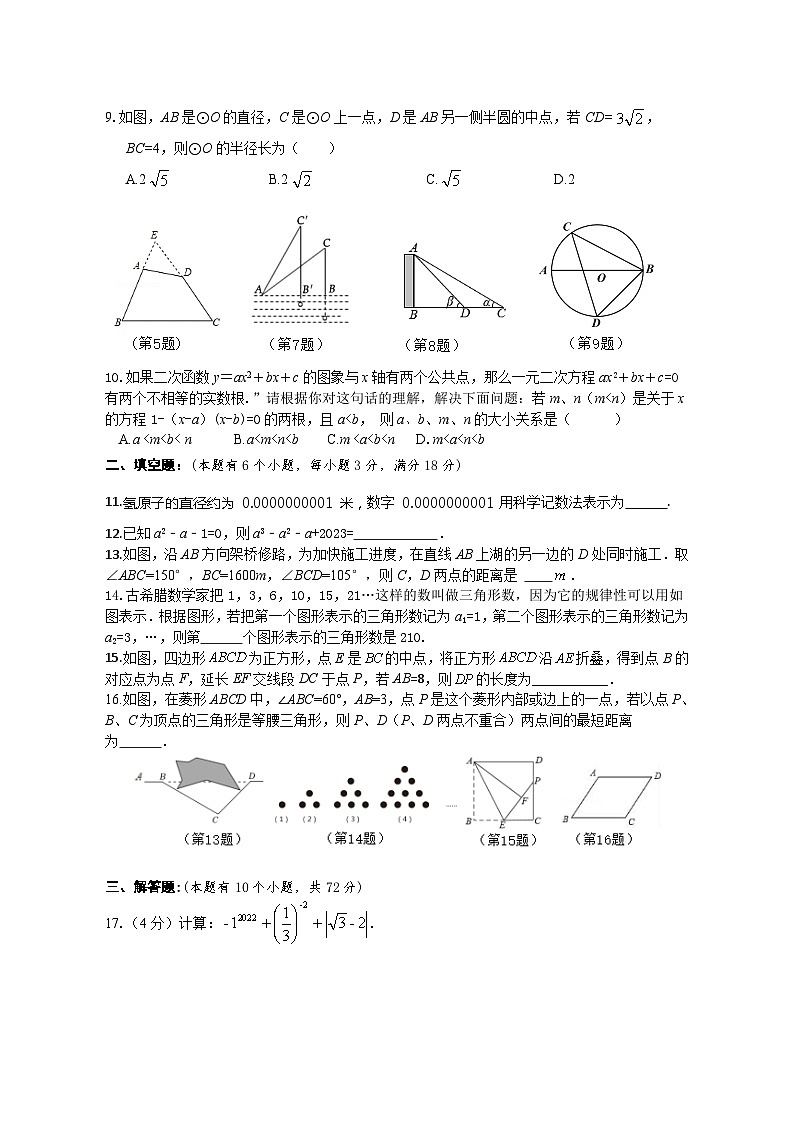
郧西县2023年5月九年级学业水平监测数 学 试 题一、选择题：（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.1．一个数的相反数是3，这个数是（　　）A. -3            B.            C.3             D.2.如图所示的物体的左视图为（     ）  3．下列运算正确的是(    )A.    B.    C.  D.4．在学校举行的运动会上，小明和小亮报名参加百米赛跑，预赛分甲、乙、丙、丁四组进行，运动员通过抽签来确定要参加的预赛小组，小明和小亮恰好抽到同一组的概率是（    ）A.             B.             C.       D. 5.如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P（　　）A.有且只有1个                B. 有且只有2个  C. 组成∠E的角平分线         D.组成∠E的角平分线所在的直线（E点除外）6.《九章算术》卷八方程第十题原文为：“今有甲、乙二人持钱不知其数甲得乙半而钱五十，乙得甲太半而亦钱五十.问：甲、乙持钱各几何？”题目大意是：甲、乙两人各带了若干钱.如果甲得到乙所有钱的一半，那么甲共有钱50；如果乙得到甲所有钱的，那么乙也共有钱50，问：甲、乙两人各带了多少钱？设甲、乙两人持钱的数量分别为x，y，则可列方程组为（    ） A． B． C． D．7.已知钓鱼杆AC的长为10米，露在水上的鱼线BC长为6m，某钓鱼者想看看鱼钩上的情况，把鱼竿AC 转动到ACˈ的位置，此时露在水面上的鱼线BʹCʹ 长度为8米，则BBʹ的长为(  ）  A. 4米             B.3米              C.2米              D.1米  8.如图，已知点B，D，C在同一直线的水平，在点C处测得建筑物AB的顶端A的仰角为α，在点D处测得建筑物AB的顶端A的仰角为β，CD=a，则建筑物AB的高度为（ )  A．    B．    C．    D．  9.如图，AB是⊙O的直径，C是⊙O上一点，D是AB另一侧半圆的中点，若CD=，BC=4，则⊙O的半径长为（    ）A.2              B.2                C.             D.2      10.如果二次函数y＝ax2＋bx＋c的图象与x轴有两个公共点，那么一元二次方程ax2＋bx＋c=0有两个不相等的实数根.”请根据你对这句话的理解，解决下面问题：若m、n（m<n）是关于x的方程1-（x-a）(x-b)=0的两根，且a<b， 则a、b、m、n的大小关系是（   ） A.a <m<b< n      B.a<m<n<b    C.m <a<b<n   D.m<a<n<b二、填空题：(本题有6个小题，每小题3分，满分18分)11.氢原子的直径约为 0.0000000001米，数字 0.0000000001用科学记数法表示为      .12.已知a2﹣a﹣1=0，则a3﹣a2﹣a+2023=            ．13.如图，沿AB方向架桥修路，为加快施工进度，在直线AB上湖的另一边的D处同时施工．取∠ABC=150°，BC=1600m，∠BCD=105°，则C，D两点的距离是 　　．14.古希腊数学家把1，3，6，10，15，21…这样的数叫做三角形数，因为它的规律性可以用如图表示．根据图形，若把第一个图形表示的三角形数记为a1=1，第二个图形表示的三角形数记为a2=3，…，则第      个图形表示的三角形数是210.15.如图，四边形为正方形，点E是的中点，将正方形沿折叠，得到点B的对应点为点F，延长EF交线段DC于点P，若AB=8，则的长度为___________．16.如图，在菱形ABCD中，∠ABC=60°，AB=3，点P是这个菱形内部或边上的一点，若以点P、B、C为顶点的三角形是等腰三角形，则P、D（P、D两点不重合）两点间的最短距离为　  　． 三、解答题:(本题有10个小题，共72分)17.（4分）计算：.  18.（6分）化简： . 19.(9分)某中学数学兴趣小组为了解本校学生对A：新闻、B：体育、C：动画、D：娱乐、E：戏曲五类电视节目的喜爱情况，随机抽取了部分学生进行调查（被调查的学生只选一类并且没有不选的），并将调查结果绘制成如图所示的不完整的条形图和扇形图．请根据图中所给出的信息解答下列问题：（1）本次抽样调查的样本容量是__________；（2）请补全条形图；（3）扇形图中，_________，节目类型E对应的扇形圆心角的度数是__________；（4）若该中学有1800名学生，那么该校喜欢新闻类节目的学生大约有多少人？  20.（6分））如图，一次函数y=x+m的图象与反比例函数的图象交于A，B两点，且与x轴交于点C，点A的坐标为（2，1）．（1）求m及k的值；（2）求点C的坐标，并结合图象写出不等式组0＜x+m≤的解集．  21.（7分）如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，且AF=CE=AE．⑴说明四边形ACEF是平行四边形；⑵当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．     22.（8分）如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O，使⊙O经过点A和点D,且交AB于E.（1）判断直线BC与⊙O的位置关系，并说明理由；（2）若AC=3，，求图中阴影部分的面积（结果保留根号和）.  23.（10分）某公司开发出一种产品，投资2500万元一次性购买整套生产设备，此外生产每件产品需成本20元，每年还需投入500万厂告费，按规定该产品的售价不得低于30元/件且不得高于70元/件，该产品的年销售量y(万件)与售价x(元/件) 之间的函数关系如下表: x（元/件） 30 31… 70 y（万件） 120 119… 80(1)求y与x的函数关系式，并写出x的取值范围；(2) 第一年公司是盈利还是亏损？并求出当盈利最大或亏损最小时该产品的售价；(3)在 (2)的前提下，即在第一年盈利最大或亏损最小时，第二年公司重新确定产品定价，使两年共盈利不低于3500万元，求第二年产品售价的取值范围.   24.（10分）在Rt△ABC中，AC＝BC，将线段CA绕点C旋转α（0°＜α＜90°），得到线段CD，连接AD、BD．(1)如图1，将线段CA绕点C逆时针旋转α，则∠ADB的度数为 　   　；(2)将线段CA绕点C顺时针旋转α时，在图2中依题意补全图形，并求∠ADB的度数；（3）在（2）的条件下，若∠BCD的平分线CE交BD于点F，交DA的延长线于点E，连结BE．用等式表示线段AD、CE、BE之间的数量关系，并证明．        25.（12分）已知抛物线y =ax2+bx +3与x轴交于A(-1,0)、B(3,0)两点，与y轴交于点C,如图1所示.(1)求抛物线的解析式；(2)将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），求h的取值范围；(3)设点P是x轴上方的抛物线上任一点，点Q在直线x =-3上，△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能，求出符合条件的点P的坐标:若不能，请说明理由.     答案及评分标准一、选择题：1-10：  AABBDCCDCC三、解答题:11.1×10-10        12.2023      13.     14.20     15.      16.三、解答题：17.原式=-1+9+2-.....................................3分       =10-......................................4分 18.原式=......................................2分       =......................................4分    =.......................................6分19.（1）300；…………………………………………2分（2）补全统计图如下：…………………………………………3分（3）35, 18；……………………………………………………………………7分（4）该校1800名学生中喜欢新闻类节目的学生有：（人）．……………………………………………………9分 20.（1）由题意可得：点A（2，1）在函数y=x+m的图象上，∴2+m=1即m=﹣1，………………………………………………1分∵A（2，1）在反比例函数的图象上，∴∴k=2；……………………………………………………2分（2）∵一次函数解析式为y=x﹣1，令y=0，得x=1，∴点C的坐标是（1，0），………………………………………………4分由图象可知不等式组0＜x+m≤的解集为1＜x≤2．……………………6分 21.（1）证明：由题意知∠FDC =∠DCA = 90°．∴EF∥CA   ∴∠AEF =∠EAC∵AF = CE = AE  ∴∠F =∠AEF =∠EAC =∠ECA    又∵AE = EA∴△AEC≌△EAF，…………………………………………2分∴EF = CA，∴四边形ACEF是平行四边形 ．…………………………………………4分（2）当∠B=30°时，四边形ACEF是菱形 ．…………………………5分理由是：∵∠B=30°，∠ACB=90°，∴AC=，∵DE垂直平分BC，∴ BE=CE又∵AE=CE，∴CE=，∴AC=CE，∴四边形ACEF是菱形．………………………………………………7分 22.(1)连结OD，∵OA=OD，∴∠1=∠3，∵AD平分∠BAC，∴∠1=∠2，  而∠2=∠3，∴∠2=∠3，∴OD∥AC，∴∠ODB=∠C=90°…………………………………………………………3分即OD⊥BC， 又OD是⊙O半径∴BC是⊙O的切线；……………………………………………………4分（2）过点O作AC的垂线段OH，则OH∥BC，⸪AC=3，CD=,Rt△ACD中,tan∠2==     ⸫∠2=30°,…………………………1分⸫∠CAB=60°,∠B=30°，∠AOH=30°⸫AH=AO，矩形CDOH中，CH=OD，而OD=OA，∵AC=AH+CH，即3=AO+AO， ∴AO=2，即⊙O的半径为2；…………………………6分Rt△OBD中，∠BOD=90°－∠B=60°，则BD=DO·tan60°=，，，∴……………………………………………………8分 23.（1）y=120-x−301×1=-x+150（30≤x≤70）；………………………………2分（2）设公司第一年的盈利为w万元，则w=y（x-20）-2500-500=（-x+150）（x-20）-3000=-（x-85）2+1225≤1225．∴第一年公司盈利了．∵30≤x≤70，∴当x=70时，w最大=1000⸫当商品售价定为70元/件时，盈利最大，最大盈利为1000万元.答：第一年公司是盈利了，当盈利最大时该产品的售价70元/件.…………………………6分（3）由题意知：（-x+150）（x-20）+1000-500≥3500-（x-85）2≥-1225,令-（x-85）2=-1225，解得x=120或x=50⸫-（x-85）2≥-1225 解集为50≤x≤120,又30≤x≤70，⸫第二年产品售价的取值范围为：50≤x≤70………………………………………………10分24（1）135°；…………………………………………………………2分(2)补全图形，如图：由题意得：,⸫=45°………………………………………………………………6分（3）2BE-AD=CE．……………………………………………………7分理由如下：过点C作CH⊥EC于点C，交ED的延长线于点H，如图：∵CD=CB，CE是∠BCD的平分线，∴CE是线段BD的垂直平分线，∴BE=DE，∠EFD=90°，由①知∠ADB=45°，∴∠DEF=45°，∴△CEH是等腰直角三角形， ∴∠DEF=∠H=45°，CE=CH，∵CD=CA，∴∠CAD=∠CDA，则∠CAE=∠CDH，∴△AEC≌△DHC，∴AE=DH，∴EH=2ED-AD=2BE-AD，∵△CEH是等腰直角三角形，∴2BE-AD=CE．………………………………………………………………10分25.（1）∵抛物线的对称轴x=1，B（3，0），∴A（﹣1，0）∵抛物线y=ax2+bx+c过点C（0，3）∴当x=0时，c=3．又∵抛物线y=ax2+bx+c过点A（﹣1，0），B（3，0），∴抛物线的解析式为：y=﹣x2+2x+3；…………………………………………3分（2）∵C（0，3），B（3，0），∴直线BC解析式为y=﹣x+3，∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点坐标为（1，4）∵对于直线BC：y=﹣x+1，当x=1时，y=2；将抛物线L向下平移h个单位长度，∴当h=2时，抛物线顶点落在BC上；当h=4时，抛物线顶点落在OB上，∴将抛物线L向下平移h个单位长度，使平移后所得抛物线的顶点落在△OBC内（包括△OBC的边界），则2≤h≤4；………………………………………………………………8分（3）设P（m，﹣m2+2m+3），Q（﹣3，n），P点在x轴上方，过P点作PM垂直于y轴，交y轴与M点，过B点作BN垂直于MP的延长线于N点，如图所示：∵B（3，0），∵△PBQ是以点P为直角顶点的等腰直角三角形，∴∠BPQ=90°，BP=PQ，则∠PMQ=∠BNP=90°，∠MPQ=∠NBP，在△PQM和△BPN中，，∴△PQM≌△BPN（AAS），∴PM=BN，∵PM=BN=﹣m2+2m+3，根据B点坐标可得PN=3﹣m，且PM+PN=6，∴﹣m2+2m+3+3﹣m=6，解得：m=1或m=0，∴P（1，4）或P（0，3）．…………………………………………………………12分