









浙教版九年级上册4.1 比例线段优质ppt课件
展开4.1比例线段(3) 学案
课题 | 4.1比例线段(3) | 单元 | 第四单元 | 学科 | 数学 | 年级 | 九年级上册 |
学习 目标 | 1. 理解比例中项的概念,并能进行简单的计算; 2.了解黄金分割的概念及其在实际生活中的应用. | ||||||
重点 | 黄金分割的概念及其简单应用.
| ||||||
难点 | 例5的作图牵涉到线段的倍分关系与和差关系,比较复杂,是本节教学的难点. | ||||||
教学过程 |
导入新课 | 【引入思考】 想一想 已知a=2,b=2算一算,成立吗?a,b,b,c这四个数成比例吗?再写出三个数,使它们满足的条件 总结:一般地,如果三个数 a、b、c满足比例式,(或 a:b=b:c),那么b就叫做a,c的 . 用符号语言表示为: . 学以致用 1. 1是不是 的比例中项?如果是比例中项,请写出相应的比例式. 2. 2和8的比例中项是________
|
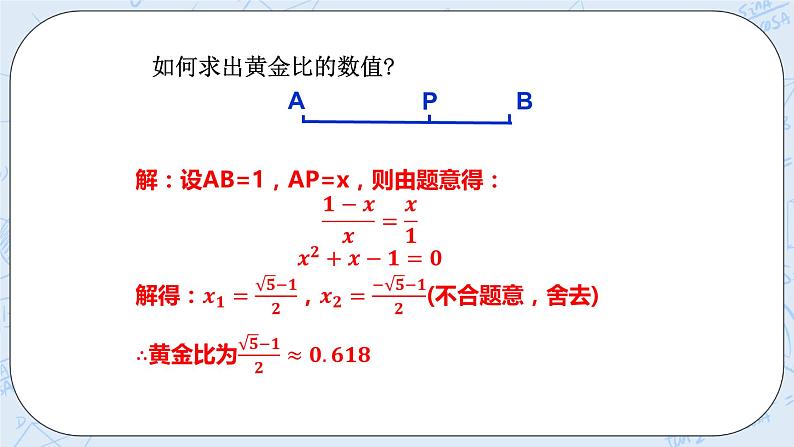
新知讲解 | 提炼概念 著名画家达•芬奇的名画《蒙娜丽莎》,画中脸部被围在矩形ABCD中,图中四边形BCEF为正方形,而在线段上的点F把线段AB分成两条线段,其中 如图,如果点P把线段AB分成2条线段AP和BP,使,那么称线段AB被点P ,线段AP与AB的比叫 ,点P叫线段AB的 . 如何求出黄金比的数值?
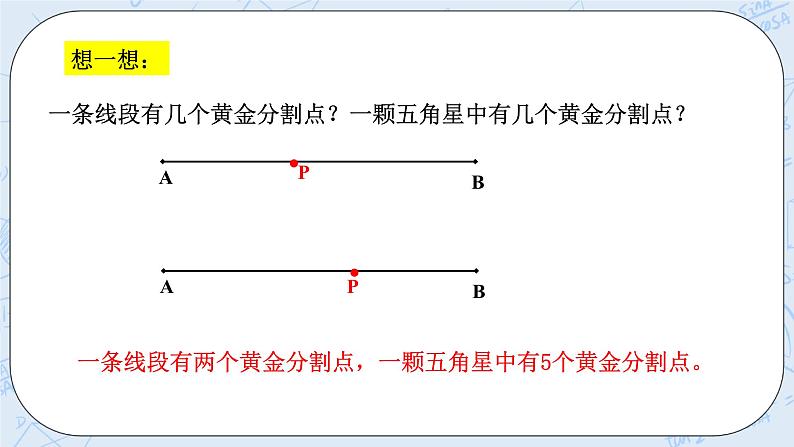
想一想: 一条线段有几个黄金分割点?一颗五角星中有几个黄金分割点?
典例精讲 例5 如图,已知线段,点P是它的黄 金分割点,AP>PB . 求AP,PB的长.
|
课堂练习 | 巩固训练 1.已知线段a=4,b=16,线段c是a,b的比例中项,那么c等于 ( ) A.10 B.8 C.-8 D.±8 2.若线段MN的长为2 cm,点P是线段MN的黄金分割点,则较长的线段MP的长为 ( ) A.(-1)cm B. cm C.(3-)cm D. cm 3.若x是8和4的比例中项,则x=________.
4.若点C是线段AB上,且满足条件________ (填写比例式),那么C是AB的黄金分割点.
5.如图所示,要设计一座1 m高的抽象人物雕塑,使雕塑的上部(腰以上)AB与下部(腰以下)BC的高度比等于下部与全部(全身)AC的高度比,雕塑的下部应设计为多高?
答案: 引入思考 想一想: 比例中项. 用符号语言表示为: =<=>b2=ac. 学以致用
提炼概念 如图,如果点P把线段AB分成2条线段AP和BP,使,那么称线段AB被点P黄金分割,线段AP与AB的比叫黄金比,点P叫线段AB的黄金分割点. 如何求出黄金比的数值? 解:设AB=1,AP=x,则由题意得: 解得:,(不合题意,舍去) 黄金比为 一条线段有两个黄金分割点,一颗五角星中有5个黄金分割点。
典例精讲 解:因为点P是线段AB的黄金分割点,且AP>PB
巩固训练 1.答案:B 2.答案:A 3.±4. 4.BC/AC=AC/AB 5.解:设雕塑的下部应设计为x m, 则根据题意得:=, 解得:x=. 答:雕塑的下部应设计为 m.
|
课堂小结 | 1.比例中项的概念 定义:如果三个数a,b,c满足比例式__________(或a∶b=b∶c),则b叫做a,c的比例中项. 公式:=⇔b2=ac. 2.黄金分割的概念
定义:如果点P把线段AB分成两条线段AP和PB,使AP>PB,且=,那么称线段AB被点P黄金分割,点P叫做线段AB的黄金分割点,线段AP与AB的比叫做黄金比.( 黄金数:若点P是AB的黄金分割点,则=≈0.618,在数学上称为黄金数.
|
初中数学浙教版九年级上册4.2 由平行线截得的比例线段完美版ppt课件: 这是一份初中数学浙教版九年级上册4.2 由平行线截得的比例线段完美版ppt课件,文件包含浙教版数学九上42由平行线截得的比例线段课件pptx、浙教版数学九上42由平行线截得的比例线段教案doc、浙教版数学九上42由平行线截得的比例线段学案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学4.1 比例线段完美版ppt课件: 这是一份初中数学4.1 比例线段完美版ppt课件,文件包含浙教版数学九上412比例线段课件pptx、浙教版数学九上412比例线段教案doc、浙教版数学九上412比例线段学案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学浙教版九年级上册4.1 比例线段优秀ppt课件: 这是一份初中数学浙教版九年级上册4.1 比例线段优秀ppt课件,文件包含浙教版数学九上411比例线段课件pptx、浙教版数学九上411比例线段学案doc、浙教版数学九上411比例线段教案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。













