中考数学三轮冲刺《二次函数压轴题》强化练习三（含答案）

这是一份中考数学三轮冲刺《二次函数压轴题》强化练习三（含答案），共17页。
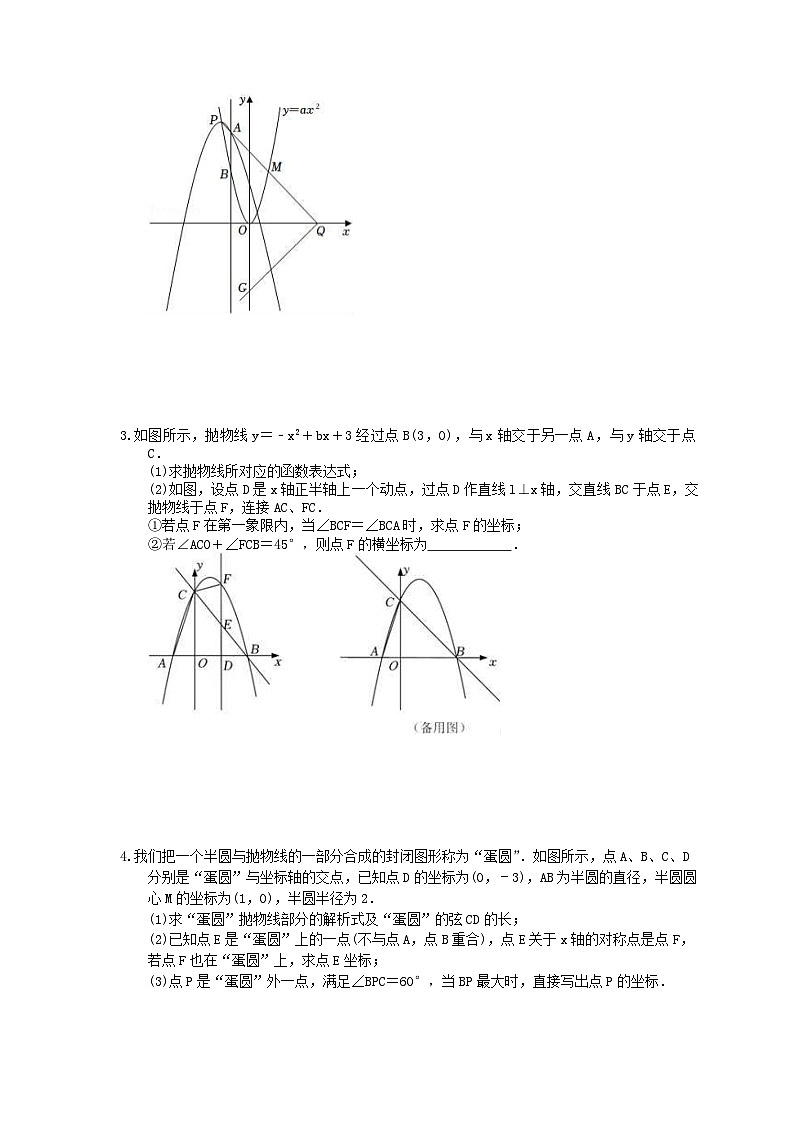
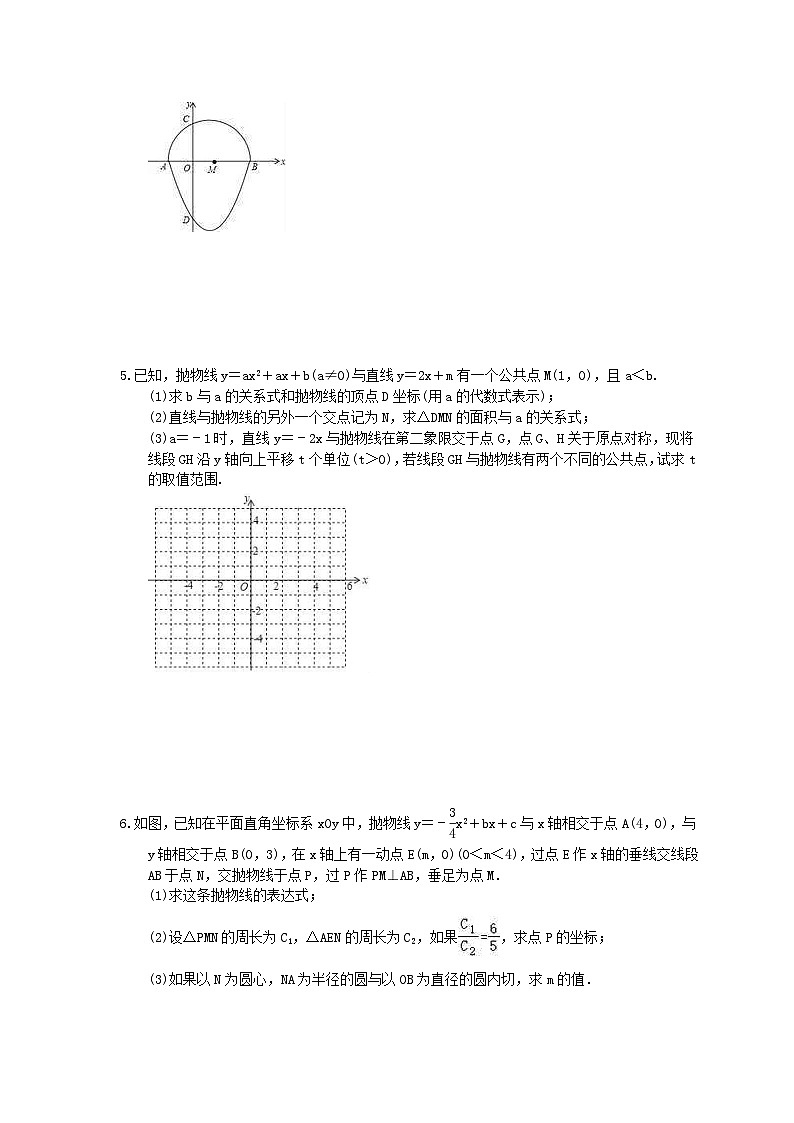
中考数学三轮冲刺《二次函数压轴题》强化练习三1.如图，已知点(0，)在抛物线C1：y＝x2＋bx＋c上，且该抛物线与x轴正半轴有且只有一个交点A，与y轴交于点B，点O为坐标原点．(1)求抛物线C1的解析式；(2)抛物线C1沿射线BA的方向平移个单位得到抛物线C2，如图2，抛物线C2与x轴交于C，D两点，与y轴交于点E，点M在抛物线C2上，且在线段ED的下方，作MN∥y轴交线段DE于点N，连接ON，记△EMD的面积为S1，△EON的面积为S2，求S1＋2S2的最大值；(3)如图3，在(2)的条件下，抛物线C2的对称轴与x轴交于点F，连接EF，点P在抛物线C2上且在对称轴的右侧，满足∠PEC＝∠EFO．①直接写出P点坐标；②是否在抛物线C2的对称轴上存在点H，使得△PDH为等腰三角形，若存在，请直接写出H点的坐标；若不存在请说明理由．      2.如图，在平面直角坐标系xOy中，抛物线E：y＝﹣(x﹣m)2＋2m2(m＜0)的顶点P在抛物线F：y＝ax2上，直线x＝t与抛物线E，F分别交于点A，B．(1)求a的值；(2)将A，B的纵坐标分别记为yA，yB，设s＝yA﹣yB，若s的最大值为4，则m的值是多少？(3)Q是x轴的正半轴上一点，且PQ的中点M恰好在抛物线F上．试探究：此时无论m为何负值，在y轴的负半轴上是否存在定点G，使∠PQG总为直角？若存在，请求出点G的坐标；若不存在，请说明理由．      3.如图所示，抛物线y＝﹣x2＋bx＋3经过点B(3，0)，与x轴交于另一点A，与y轴交于点C．(1)求抛物线所对应的函数表达式；(2)如图，设点D是x轴正半轴上一个动点，过点D作直线l⊥x轴，交直线BC于点E，交抛物线于点F，连接AC、FC．①若点F在第一象限内，当∠BCF＝∠BCA时，求点F的坐标；②若∠ACO＋∠FCB＝45°，则点F的横坐标为            ．      4.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”．如图所示，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为(0，﹣3)，AB为半圆的直径，半圆圆心M的坐标为(1，0)，半圆半径为2．(1)求“蛋圆”抛物线部分的解析式及“蛋圆”的弦CD的长；(2)已知点E是“蛋圆”上的一点(不与点A，点B重合)，点E关于x轴的对称点是点F，若点F也在“蛋圆”上，求点E坐标；(3)点P是“蛋圆”外一点，满足∠BPC＝60°，当BP最大时，直接写出点P的坐标．      5.已知，抛物线y＝ax2＋ax＋b(a≠0)与直线y＝2x＋m有一个公共点M(1，0)，且a＜b.(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示)；(2)直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；(3)a＝﹣1时，直线y＝﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位(t＞0)，若线段GH与抛物线有两个不同的公共点，试求t的取值范围.      6.如图，已知在平面直角坐标系xOy中，抛物线y＝﹣x2＋bx＋c与x轴相交于点A(4，0)，与y轴相交于点B(0，3)，在x轴上有一动点E(m，0)(0＜m＜4)，过点E作x轴的垂线交线段AB于点N，交抛物线于点P，过P作PM⊥AB，垂足为点M．(1)求这条抛物线的表达式；(2)设△PMN的周长为C1，△AEN的周长为C2，如果，求点P的坐标；(3)如果以N为圆心，NA为半径的圆与以OB为直径的圆内切，求m的值．      7.如图，抛物线y＝﹣x2＋bx＋c经过点A，B，C，已知点A(﹣1，0)，点C(0，3).(1)求抛物线的表达式；(2)P为线段BC上一点，过点P作y轴的平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；(3)设E是抛物线上的一点，在x轴上是否存在点F，使得A，C，E，F为顶点的四边形是平行四边形？若存在，求点E，F的坐标；若不存在，请说明理由.      8.在平面直角坐标系xOy中，已知抛物线y＝﹣＋bx2＋c经过点A(﹣1，0)和点B(0，)，顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．(1)求这条抛物线的表达式；(2)求线段CD的长；(3)将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．      
0.中考数学三轮冲刺《二次函数压轴题》强化练习三（含答案）答案解析  一         、综合题1.解：(1)∵点(0,)在抛物线C1：y＝x2＋bx＋c上，∴c＝．∵该抛物线与x轴正半轴有且只有一个交点A，∴b＜0，b2﹣4××＝0．∴b＝﹣．∴抛物线C1的解析式为y＝x2﹣x＋．(2)∵y＝＝x2﹣x＋＝(x﹣1)2，又∵抛物线C1沿射线BA的方向平移个单位得到抛物线C2，∴抛物线C2的解析式为y＝(x﹣1)2﹣＝x2﹣x＋2，令x＝0，则y＝2，∴E(0，2)．∴OE＝2．令y＝0，则x2﹣x＋2＝0，解得：x＝1或3，∴C(1，0)，D(3，0)．∴OC＝1，OD＝3，∴CD＝2．∵点M在抛物线C2上，∴设M(m，m2﹣m＋2)，设直线ED的解析式为y＝kx＋n，∴，解得：，∴直线ED的解析式为y＝﹣x＋2．∵MN∥y轴交线段DE于点N，∴N(m，﹣m＋2)，∵点M在线段ED的下方，∴MN＝﹣x＋2﹣(m2﹣m＋2)＝﹣m2＋2m，∵S△EMD＝S△EMN＋S△DMN＝×MN•OD＝﹣m2＋3m，S△EON=OE×m＝m，∴S1＋2S2＝﹣m2＋2m＋2m＝﹣m2＋4m＝﹣(m﹣2)2＋4，∵﹣1＜0，∴当m＝2时，S1＋2S2有最大值4；(3)①点P的坐标为(，)，理由：设直线EP与x轴交于点G，如图，∵抛物线C2的解析式为y＝(x﹣1)2﹣，∴抛物线的对称轴为直线x＝2，∴F(2，0)．∴OF＝2．∵OC＝1，∴CF＝OF﹣OC＝1．EC＝＝，∵∠PEC＝∠EFO，∠PEC＝∠PEF＋∠CEF，∠EFO＝∠PEF＋∠G，∴∠CEF＝∠G．∵∠ECF＝∠GCE，∴△ECF∽△GCE，∴．∴CE2＝CF•CG，∴CG＝5，∴OG＝OC＋CG＝6，∴G(6，0)．设直线EG的解析式为y＝ax＋2，∴6a＋2＝0，∴a＝﹣．∴直线EG的解析式为y＝﹣x＋2，∴，解得：或，∴P(，)；②在抛物线C2的对称轴上存在点H，使得△PDH为等腰三角形，理由：过点P作PG⊥抛物线对称轴与点G，PH⊥x轴于点H，连接PD，如图，∵P(，)，∴OK＝，PK＝，∴DK＝OK﹣OD＝，PG＝KF＝OK﹣OF＝，∴DP＝＝＜1，∵DF＝1，∴抛物线C2的对称轴上不存在点H，使得HD＝DP，HP＝PD；当HP＝HD时，设H(2，h)，则HF＝h，过点P作PG⊥抛物线对称轴与点G，如图，则PG＝KF＝OK﹣OF＝，GF＝，∵HP＝HD，∴＝．∴12＋h2＝＋，解得：h＝，∴H(2，)．综上，在抛物线C2的对称轴上存在点H，使得△PDH为等腰三角形，点H的坐标为(2，)． 2.解：(1)由题意可知，抛物线E：y＝﹣(x﹣m)2＋2m2(m＜0)的顶点P的坐标为(m，2m2)，∵点P在抛物线F：y＝ax2上，∴am2＝2m2，∴a＝2．(2)∵直线x＝t与抛物线E，F分别交于点A，B，∴yA＝﹣(t﹣m)2＋2m2＝﹣t2＋2mt＋m2，yB＝2t2，∴s＝yA﹣yB＝﹣t2＋2mt＋m2﹣2t2＝﹣3t2＋2mt＋m2＝﹣3(t﹣m)2＋m2，∵﹣3＜0，∴当t＝m时，s的最大值为m2，∵s的最大值为4，∴m2＝4，解得m＝±，∵m＜0，∴m＝﹣．(3)存在，理由如下：设点M的坐标为n，则M(n，2n2)，∴Q(2n﹣m，4n2﹣2m2)，∵点Q在x轴正半轴上，∴2n﹣m＞0且4n2﹣2m2＝0，∴n＝﹣m，∴M(﹣m，m2)，Q(﹣m﹣m，0)．如图，过点Q作x轴的垂线KN，分别过点P，G作x轴的平行线，与KN分别交于K，N，∴∠K＝∠N＝90°，∠QPK＋∠PQK＝90°，∵∠PQG＝90°，∴∠PQK＋∠GQN＝90°，∴∠QPK＝∠GQN，∴△PKQ∽△QNG，∴PK：QN＝KQ：GN，即PKGN＝KQQN．∵PK＝﹣m﹣m﹣m＝﹣m﹣2m，KQ＝2m2，GN＝﹣m﹣m，∴(﹣m﹣2m)(﹣m﹣m)＝2m2QN，解得QN＝+2．∴G(0，﹣﹣2)． 3.解：(1)∵B(3，0)在抛物线y＝﹣x2＋bx＋3上，∴﹣32＋3b＋3＝0，∴b＝2，∴抛物线所对应的函数表达式为y＝﹣x2＋2x＋3；(2)①作点A关于直线BC的对称点G，AG交BC于点H，过点H作HI⊥x轴于点I，连接CG交抛物线于点F，此时，∠BCF＝∠BCA，y＝﹣x2＋2x＋3，令x＝0，则y＝3，令y＝0，则﹣x2＋2x＋3＝0，解得：x＝3或＝﹣1，∴A(﹣1，0)，B(3，0)，C(0，3)．∴OB＝OC，AB＝4，∴△OCB是等腰直角三角形，则∠OCB＝∠OBC＝45°，∴∠HAB＝∠OBC＝∠AHI＝∠BHI＝45°，∴HI＝AI＝BI＝AB＝2，∴H(1，2)，∴G(3，4)，设直线CG的解析式为y＝kx＋3，把G(3，4)代入得：4＝3k＋3，解得k＝，∴直线CF的解析式为y＝x＋3，∴，解得，∴点F的坐标为(，)；②当点F在x轴上方时，如图，延长CF交x轴于N，∵点B(3，0)，点C(0，3)，∴OB＝OC，∴∠OCB＝∠OBC＝45°，∵A(﹣1，0)，∴OA＝1，∵∠ACO＋∠FCB＝45°，∠CBO＝∠FCB＋∠CNO＝45°．∴∠ACO＝∠CNO，∵∠COA＝∠CON＝90°，∴△CAO∽△NCO，∴，∴，∴ON＝9，∴点N(9，0)，设直线CF的解析式为y＝k′x＋3，把N(9，0)代入得：0＝9k′＋3，解得k′＝﹣，∴直线CF的解析式为y＝﹣x＋3，∴﹣x＋3＝﹣x2＋2x＋3，∴x1＝0(舍去)，x2＝，∴点的横坐标为；当点F在x轴下方时，如图，设CF与x轴交于点M，∵∠ACO＋∠FCB＝45°，∠FCB＋∠OCM＝45°．∴∠ACO＝∠OCM，∵OC＝OC，∠COA＝∠COM＝90°，∴△CAO≌△CMO(ASA)，∴OM＝OA＝1，∴点M(1，0)，同理直线CF解析式为：y＝﹣3x＋3．∴﹣3x＋3＝﹣x2＋2x＋3，∴x1＝0(舍去)，x2＝5，∴点的横坐标为5．综上所述，点F的横坐标为或5．故答案为：或5． 4.解：(1)∵半圆圆心M的坐标为(1，0)，半圆半径为2．∴A(﹣1，0)，B(3，0)，设抛物线为y＝a(x＋1)(x﹣3)，∵抛物线过D(0，﹣3)，∴﹣3＝a(0＋1)(0﹣3)，解得a＝1，y＝(x＋1)(x﹣3)，即y＝x2﹣2x﹣3(﹣1≤x≤3)；连接AC，BC，∵AB为半圆的直径，∴∠ACB＝90°，∵CO⊥AB，∴∠ACO＋∠OCB＝∠OCB＋∠OBC＝90°，∴∠ACO＝∠OBC，∴△ACO∽△CBO，∴，∴CO2＝AOBO＝3，∴CO＝，∴CD＝CO＋OD＝3＋；(2)假设点E在x轴上方的“蛋圆”上，设E(m，n)，则点F的坐标为(m，﹣n)．EF与x轴交于点H，连接EM．∴HM2＋EH2＝EM2，∴(m﹣1)2＋n2＝4，…①；∵点F在二次函数y＝x2﹣2x﹣3的图象上，∴m2﹣2m﹣3＝﹣n，…②；解由①②组成的方程组得：；．(n＝0舍去)由对称性可得：；．∴E1(1＋，1)，E2(1﹣，1)，E3(1＋，-1)，E4(1﹣，-1)．(3)如图4，∵∠BPC＝60°保持不变，因此点P在一圆弧上运动．此圆是以K为圆心(K在BC的垂直平分线上，且∠BKC＝120°)，BK为半径．当BP为直径时，BP最大．在Rt△PCR中可求得PR＝1，RC＝．所以点P的坐标为(1，2)． 5.解：(1)∵抛物线y＝ax2＋ax＋b有一个公共点M(1，0)，∴a＋a＋b＝0，即b＝﹣2a，∴y＝ax2＋ax＋b＝ax2＋ax﹣2a＝a(x＋)2﹣a，∴抛物线顶点D的坐标为(﹣，﹣a)；(2)∵直线y＝2x＋m经过点M(1，0)，∴0＝2×1＋m，解得m＝﹣2，∴y＝2x﹣2，则，得ax2＋(a﹣2)x﹣2a＋2＝0，∴(x﹣1)(ax＋2a﹣2)＝0，解得x＝1或x＝﹣2，∴N点坐标为(﹣2，﹣6)，∵a＜b，即a＜﹣2a，∴a＜0，如图1，设抛物线对称轴交直线于点E，∵抛物线对称轴为x＝﹣，∴E(﹣，﹣3)，∵M(1，0)，N(﹣2，﹣6)，设△DMN的面积为S，∴S＝S△DEN＋S△DEM＝|(﹣2)﹣1|•|﹣﹣(﹣3)|＝，(3)当a＝﹣1时，抛物线的解析式为：y＝﹣x2﹣x＋2＝﹣(x＋)2＋，有，﹣x2﹣x＋2＝﹣2x，解得：x1＝2，x2＝﹣1，∴G(﹣1，2)，∵点G、H关于原点对称，∴H(1，﹣2)，设直线GH平移后的解析式为：y＝﹣2x＋t，﹣x2﹣x＋2＝﹣2x＋t，x2﹣x﹣2＋t＝0，△＝1﹣4(t﹣2)＝0，t＝，当点H平移后落在抛物线上时，坐标为(1，0)，把(1，0)代入y＝﹣2x＋t，t＝2，∴当线段GH与抛物线有两个不同的公共点，t的取值范围是2≤t＜. 6.解，(1)∵抛物线y＝﹣x2＋bx＋c与x轴交于点A(4，0)，与y轴交于点C(0，3)，∴∴∴抛物线的表达式为y＝﹣x2＋x＋c；(2)如图1，∵PM⊥AB，PE⊥x轴，∴∠PMN＝∠PEA＝90°，又∵∠PNM＝∠ANE，∴△PMN∽△AEN．∴．即．又∵，∴．设直线AB：y＝kx＋b，又直线AB经过点A(4，0)，点B(0，3)，∴∴∴y＝﹣x＋3．∵点P在抛物线y＝﹣x2＋x＋3上，∴设点P(m，﹣m2＋m＋3)(0＜m＜4)，∵点N在直线y＝﹣x＋3上，设点N(m，﹣m＋3)．∴PN＝﹣m2＋m＋3﹣(﹣m＋3)＝﹣m2＋3m．又．∴，解得：m1＝2，m2＝4(不合题意，舍去)．∴点P的坐标是(2,)．(3)如图2，设OB的中点为点Q，则点Q的坐标(0,)，又点N(m,﹣m＋3)，过点N作NK⊥y轴于点K，则NK＝m，KQ＝﹣m＋3﹣＝﹣m＋，在Rt△NQK中，QN＝＝，当⊙N与⊙Q内切时，．∴＝ (4﹣m)﹣，解之得：．∴当⊙N与⊙Q内切时，． 7.解：(1)∵点A(﹣1，0)，点C(0，3)在抛物线y＝﹣x2＋bx＋c上，∴解得b＝2，c＝3.即抛物线的表达式是y＝﹣x2＋2x＋3；(2)令﹣x2＋2x＋3＝0，解得x1＝﹣1，x2＝3，∵点A(﹣1，0)，∴点B的坐标为(3，0).设过点B、C的直线的解析式为：y＝kx＋b，解得k＝﹣1，b＝3.∴过点B、C的直线的解析式为：y＝﹣x＋3.设点P的坐标为(a，﹣a＋3)，则点D的坐标为(a，﹣a2＋2a＋3)，∴PD＝(﹣a2＋2a＋3)﹣(﹣a＋3)＝﹣a2＋3a.∴S△BDC＝S△PDC＋S△PDB＝﹣(a﹣)2＋.∴当a＝时，△BDC的面积最大，∴点P的坐标为(,).(3)存在.当AC是平行四边形的边时，则点E的纵坐标为3或﹣3，∵E是抛物线上的一点，∴将y＝3代入y＝﹣x2＋2x＋3，得x1＝0(舍去)，x2＝2；将y＝﹣3代入y＝﹣x2＋2x＋3，得x3＝1＋，x4＝1﹣.∴E1(2，3)，E2(1＋，﹣3)，E3(1﹣，﹣3)，则点F1(1，0)，F2(2＋，0)，F3(2﹣，0)，当AC为平行四边形的对角线时，则点E的纵坐标为3，∵E是抛物线上的一点，∴将y＝3代入y＝﹣x2＋2x＋3，得x1＝0(舍去)，x2＝2；即点E4(2，3).则F4(﹣3，0).由上可得，点E的坐标为：E1(2，3)，E2(1＋，﹣3)，E3(1﹣，﹣3)，E4(2，3)，与之对应的点F的坐标是：F1(1，0)，F2(2＋，0)，F3(2﹣，0)，F4(﹣3，0). 8.解：(1)把A(﹣1，0)和点B(0，)代入y＝﹣x2＋bx＋c，得，解得，∴抛物线解析式为y＝﹣x2＋2x＋；(2)∵y＝﹣(x﹣2)2＋，∴C(2，)，抛物线的对称轴为直线x＝2，如图，设CD＝t，则D(2，﹣t)，∵线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处，∴∠PDC＝90°，DP＝DC＝t，∴P(2＋t，﹣t)，把P(2＋t，﹣t)代入y＝﹣x2＋2x＋得﹣(2＋t)2＋2(2＋t)＋＝﹣t，整理得t2﹣2t＝0，解得t1＝0(舍去)，t2＝2，∴线段CD的长为2；(3)P点坐标为(4，)，D点坐标为(2，)，∵抛物线平移，使其顶点C(2，)移到原点O的位置，∴抛物线向左平移2个单位，向下平移个单位，而P点(4，)向左平移2个单位，向下平移个单位得到点E，∴E点坐标为(2，﹣2)，设M(0，m)，当m＞0时，•(m＋＋2)•2＝8，解得m＝，此时M点坐标为(0，)；当m＜0时，•(﹣m＋＋2)•2＝8，解得m＝﹣，此时M点坐标为(0，﹣)；综上所述，M点的坐标为(0，)或(0，﹣)．