中考数学三轮冲刺《二次函数压轴题》强化练习十三（含答案）

这是一份中考数学三轮冲刺《二次函数压轴题》强化练习十三（含答案），共15页。
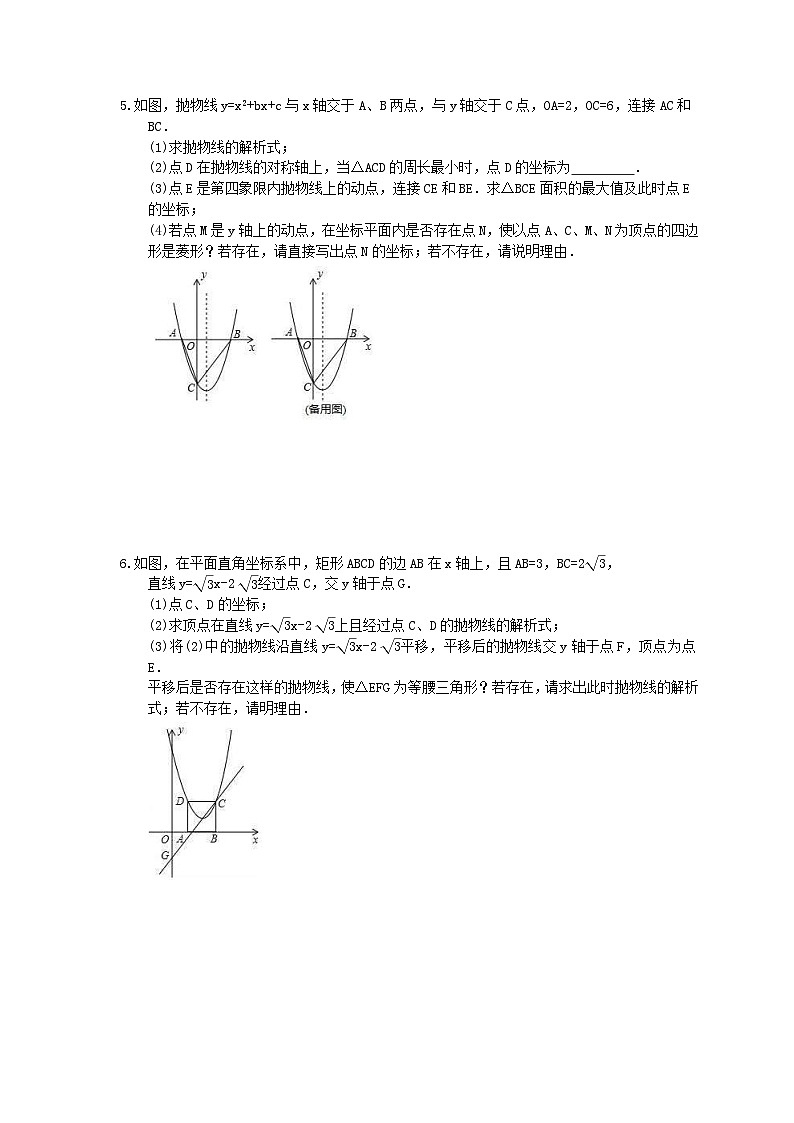
中考数学三轮冲刺《二次函数压轴题》强化练习十三1.我们规定：在正方形ABCD中，以正方形的一个顶点A为顶点，且过对角顶点C的抛物线，称为这个正方形的以A为顶点的对角抛物线．(1)在平面直角坐标系xOy中，点在轴正半轴上，点C在y轴正半轴上．①如图1，正方形OABC的边长为2，求以O为顶点的对角抛物线；②如图2，在平面直角坐标系中，正方形OABC的边长为a，其以O为顶点的对角抛物线的解析式为y＝x2，求a的值；(2)如图3，正方形ABCD的边长为4，且点A的坐标为(3，2)，正方形的四条对角抛物线在正方形ABCD内分别交于点M、P、N、Q，直接写出四边形MPNQ的形状和四边形MPNQ的对角线的交点坐标．       2.如图，在平面直角坐标系中，二次函数y＝ax2＋bx＋c的图象经过点A(﹣2，0)，B(0，)，C(1，0)，其对称轴与x轴交于点E，顶点坐标为D．(1)求二次函数的表达式；(2)点P为抛物线的对称轴上的一个动点，且在第二象限内，若平面内存在点Q，使得以B，C，P，Q为顶点的四边形为菱形，求点Q的坐标；(3)若M为y轴上的一个动点，连接ME，求MB＋ME的最小值．      3.如图，在平面直角坐标系中，抛物线y＝x2﹣bx＋c交x轴于点A，B，点B的坐标为(4，0)，与y轴于交于点C(0，﹣2)．(1)求此抛物线的解析式；(2)在抛物线上取点D，若点D的横坐标为5，求点D的坐标及∠ADB的度数；(3)在(2)的条件下，设抛物线对称轴l交x轴于点H，△ABD的外接圆圆心为M(如图1)，①求点M的坐标及⊙M的半径；②过点B作⊙M的切线交于点P(如图2)，设Q为⊙M上一动点，则在点运动过程中的值是否变化？若不变，求出其值；若变化，请说明理由．      4.如图，已知二次函数y＝﹣x2＋bx＋c经过A，B两点，BC⊥x轴于点C，且点A(﹣1，0)，C(2，0)，AC＝BC．(1)求抛物线的解析式；(2)点E是抛物线AB之间的一个动点(不与A，B重合)，求S△ABE的最大值以及此时E点的坐标；(3)根据问题(2)的条件，判断是否存在点E使得△ABE为直角三角形，如果存在，求出E点的坐标，如果不存在，说明理由．      5.如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于C点，OA=2，OC=6，连接AC和BC．(1)求抛物线的解析式；(2)点D在抛物线的对称轴上，当△ACD的周长最小时，点D的坐标为　   　．(3)点E是第四象限内抛物线上的动点，连接CE和BE．求△BCE面积的最大值及此时点E的坐标；(4)若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．      6.如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，且AB=3，BC=2，直线y=x-2经过点C，交y轴于点G．(1)点C、D的坐标；(2)求顶点在直线y=x-2上且经过点C、D的抛物线的解析式；(3)将(2)中的抛物线沿直线y=x-2平移，平移后的抛物线交y轴于点F，顶点为点E．平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请明理由．       7.如图，已知抛物线y＝ax2＋bx＋c(a≠0)与x轴交于点A(﹣1，0)，B(4，0)，与y轴交于点C(0，4).(1)求此抛物线的解析式；(2)设点P(2，n)在此抛物线上，AP交y轴于点E，连接BE，BP，请判断△BEP的形状，并说明理由；(3)设抛物线的对称轴交x轴于点D，在线段BC上是否存在点Q，使得△DBQ成为等腰直角三角形？若存在，求出点Q的坐标；若不存在，说明理由.       8.如图，抛物线y＝ax2＋bx﹣3与x轴交于A(﹣2，0)和B(4，0)两点，与y轴交于点C．(1)求抛物线的解析式；(2)当点P为直线BC下方抛物线上一动点(不与点B、C重合)，PM⊥BC于点M，PD⊥AB于点D，交直线BC于点N，当P点的坐标为何值时，PM＋PN的值最大？(3)点P在第四象限的抛物线上移动，以PC为边作正方形CPEF、当抛物线的对称轴经过点E时，求出此时点P的坐标．      
0.中考数学三轮冲刺《二次函数压轴题》强化练习十三（含答案）答案解析  一         、综合题1.解：(1)①如图1中，设O为顶点的抛物线的解析式为y＝ax2，∵过B(2，2)，∴2＝4a，∴a＝，∴所求的抛物线的解析式为y＝x2．②如图2中，设B(a，a)．则有a＝a2，解得a＝4或0(舍弃)，∴B(4，4)，∴OA＝4，∴正方形的边长为4．(2)如图3中，结论：四边形MPNQ是菱形，对角线的交点坐标为(5，4)．理由：∵正方形ABCD的边长为4，A(3，2)，∴B(7，2)，C(7，6)，D(3，6)，∴以A为顶点的对角抛物线为y＝(x﹣3)2＋2，以B为顶点的对角抛物线为y＝(x﹣7)2＋2，以C为顶点的对角抛物线为y＝﹣(x﹣7)2＋6，以D为顶点的对角抛物线为y＝﹣(x﹣3)2＋6，由可得M(5，3)，由可得N(5，5)，由可得P(3＋2，4)，由可得Q(7﹣2，4)，∴PM＝，PN＝，QN＝，QM＝，∴PM＝PN＝QN＝QM，∴四边形MPNQ是菱形，对角线的交点坐标为(5，4)． 2.解：(1)将点A、B、C的坐标代入抛物线表达式得，解得，故抛物线的表达式为y＝﹣x2﹣x＋；(2)由函数的表达式知，函数的对称轴为x＝﹣，故设点P的坐标为(，m)．∵C(1，0)，B(0，)，∴BC2＝1＋3＝4，直线BC的表达式为y＝﹣x＋，①以C为圆心BC为半径画弧与对称轴有两个交点，此时CP＝BC，则(＋1)2＋m2＝4，解得m＝±，即此时点P的坐标为P1(﹣，)或P2(﹣，﹣)(舍去)；②以B为圆心BC为半径画弧与对称轴有两个交点，此时BP＝BC，则()2＋(m﹣)2＝4，解得m1＝＋或m2＝﹣，即此时点P的坐标为P3(﹣，＋)或P4(﹣，﹣)(舍去)；③线段BC的垂直平分线与对称轴有一个交点，此时CP＝BP，则(＋1)2＋m2＝()2＋(﹣m)2，解得m＝，即此时点P的坐标为P5(﹣，)；故点P的坐标为(﹣，)或(﹣，＋)或(﹣，)；当点P的坐标为P(﹣，)时，∵BC∥PQ，故直线PQ的表达式为y＝﹣x＋t，将点P的坐标代入上式得：＝﹣×(﹣)＋t，解得t＝-，故直线PQ的表达式为y＝﹣x＋-，则设点Q的坐标为(x，y)，其中y＝﹣x＋-，由菱形的性质知，BP的中点即为CQ的中点，由中点公式得：(x﹣)＝(0＋1)，解得x＝﹣，当x＝﹣时，y＝﹣x＋-＝+，故点Q的坐标为(﹣，+)，同理可得，点P(﹣，＋)或(﹣，)时，对应的点Q的坐标分别为(，)或(，)，综上所述，满足条件的点Q的坐标为(﹣，+)或(，)或(，)；(3)如图，连接BC，作EH⊥BC于H，交OB于M，此时BM＋ME最小．理由：∵OC＝1，OB＝，∴tan∠CBO＝，∴∠CBO＝30°，∴MH＝BM，∴BM＋ME＝MH＋EM＝EH，∴此时BM＋ME最短，在Rt△CEH中，∵∠CHE＝90°，CE＝，∠HCE＝60°，∴EH＝，∴BM＋ME的最小值为． 3.解：(1)c＝﹣2，将点B的坐标代入抛物线表达式得：解b＝，∴抛物线的解析式为y＝x2﹣x﹣2；(2)当x＝5时，y＝x2﹣x﹣2＝3，故D的坐标为(5，3)，令y＝0，则x＝4(舍去)或﹣1，故点A(﹣1，0)，如图①，连接BD，作BN⊥AD于N，∵A(﹣1，0)，B(4，0)，C(0，﹣2)，∴AD＝3，BD＝，AB＝5，∵S△ABD＝＝，∴BN＝，∴sin∠BDN＝，∴∠BDN＝45°；∴∠ADB＝∠BDN＝45°；(3)①如图②，连接MA，MB，∵∠ADB＝45°，∴∠AMB＝2∠ADB＝90°，∵MA＝MB，MH⊥AB，∴AH＝BH＝HM＝，∴点M的坐标为(，)⊙M的半径为；②如图③，连接MQ，MB，∵过点B作⊙M的切线交1于点P，∴∠MBP＝90°，∵∠MBO＝45°，∴∠PBH＝45°，∴PH＝HB＝2.5，∵＝，＝，∵∠HMQ＝∠QMP，∴△HMQ∽△QMP，∴＝，∴在点Q运动过程中的值不变，其值为． 4.解：(1)∵点A(﹣1，0)，C(2，0)，∴AC＝3，OC＝2，∵AC＝BC＝3，∴B(2，3)，把A(﹣1，0)和B(2，3)代入二次函数y＝x2＋bx＋c中得：，解得：，∴二次函数的解析式为：y＝﹣x2＋2x＋3；(2)∵直线AB经过点A(﹣1，0)，B(2，3)，设直线AB的解析式为y＝kx＋b′，∴，解得：，∴直线AB的解析式为：y＝x＋1，如图，过点E作EF∥y轴交线段AB于点F，∴设点E(t，﹣t2＋2t＋3)，则F(t，t＋1)，∴EF＝﹣t2＋2t＋3﹣(t＋1)＝﹣(t﹣)2＋，∴当t＝时，EF的最大值为，∴点E的坐标为(，)，∴此时S△ABE最大，S△ABE＝•EF•(xB−xA)＝××(2＋1)＝．(3)在问题(2)的条件下，存在点E使得△ABE为直角三角形；设E(m，﹣m2＋2m＋3)，①当点A为直角顶点，过点A作AB的垂线，与AB之间的抛物线无交点，故不可能存在点E使得△ABE为以点A为直角顶点的直角三角形，②当点B为直角顶点，如下图，此时∠EBA＝90°，过点E作EG⊥CB，交CB延长线于点G，∵BC⊥x轴于点C，且AC＝BC，∴△ABC是等腰直角三角形，∠ABC＝45°，∴∠EBG＝45°，∴△BEG是等腰直角三角形，EG＝BG，∵EG的长为点E与直线BC的距离，即2﹣m，且BG＝CG﹣BC＝﹣m2＋2m＋3﹣3＝﹣m2＋2m，∴2﹣m＝＝﹣m2＋2m，解得m＝1或m＝2(舍)，∴E(1，4)；③如下图，此时∠AEB＝90°，作EM∥x轴，交CB的延长线于点M，过点A作AN⊥x轴交ME的延长线于点N，∴∠BEM＋∠AEN＝90°，∵在Rt△AEN中，∠EAN＋∠AEN＝90°，∴∠BEM＝∠EAN，∴△AEN∽△BEM，∴BM：EN＝EM：AN，∴(﹣m2＋2m)：(m＋1)＝(2﹣m)：(﹣m2＋2m＋3)，即﹣m(2﹣m)(m＋1)(m﹣3)＝(2﹣m)(m＋1)，∵2﹣m≠0，m＋1≠0，∴m2﹣3m＋1＝0，解得m＝或m＝(舍)．∴E(，)综上，根据问题(2)的条件，存在点E(1，4)或(，)使得△ABE为直角三角形． 5.解：(1)∵OA=2，OC=6∴A(﹣2，0)，C(0，﹣6)∵抛物线y=x2+bx+c过点A、C∴   解得：∴抛物线解析式为y=x2﹣x﹣6(2)∵当y=0时，x2﹣x﹣6=0，解得：x1=﹣2，x2=3∴B(3，0)，抛物线对称轴为直线x=∵点D在直线x=上，点A、B关于直线x=对称∴xD=，AD=BD∴当点B、D、C在同一直线上时，C△ACD=AC+AD+CD=AC+BD+CD=AC+BC最小设直线BC解析式为y=kx﹣6∴3k﹣6=0，解得：k=2∴直线BC：y=2x﹣6∴yD=2×﹣6=﹣5∴D(，﹣5)故答案为：(，﹣5)(3)过点E作EG⊥x轴于点G，交直线BC与点F设E(t，t2﹣t﹣6)(0＜t＜3)，则F(t，2t﹣6)∴EF=2t﹣6﹣(t2﹣t﹣6)=﹣t2+3t∴S△BCE=S△BEF+S△CEF=EF•BG+EF•OG=EF(BG+OG)=EF•OB=×3(﹣t2+3t)=﹣(t﹣)2+∴当t=时，△BCE面积最大 ∴yE=()2﹣﹣6=﹣5∴点E坐标为(，﹣5)时，△BCE面积最大，最大值为3．(4)存在点N，使以点A、C、M、N为顶点的四边形是菱形．∵A(﹣2，0)，C(0，﹣6)∴AC=2①若AC为菱形的边长，如图3，则MN∥AC且，MN=AC=2∴N1(﹣2，2)，N2(﹣2，﹣2)，N3(2，0)②若AC为菱形的对角线，如图4，则AN4∥CM4，AN4=CN4设N4(﹣2，n)∴﹣n=解得：n=﹣∴N4(﹣2，﹣)综上所述，点N坐标为(﹣2，2)，(﹣2，﹣2)，(2，0)，(﹣2，﹣)． 6.解：(1)令y=2，2=y=x-2，解得x=4，则OA=4﹣3=1，∴C(4，2)，D(1，2)；(2)由二次函数对称性得，顶点横坐标为=2.5，令x=，则y=×﹣2=，∴顶点坐标为(，)，∴设抛物线解析式为y=a(x﹣)2﹣，把点D(1，2)代入得，a=，∴解析式为y=(x﹣)2﹣；(3)设顶点E在直线上运动的横坐标为m，则E(m，m﹣2)(m＞0)∴可设解析式为y=(x﹣m)2﹣m﹣2，①当FG=EG时，FG=EG=2m，则F(0，2m﹣2)，代入解析式得：m2﹣m﹣2=2m﹣2，得m=0(舍去)，m=﹣，此时所求的解析式为：y=(x﹣﹣)2﹣3﹣；②当GE=EF时，FG=2m，则F(0，2m﹣2)，代入解析式得：m2﹣m﹣2=2m﹣2，解得m=0(舍去)，m=，此时所求的解析式为：y=(x﹣)2﹣；③当FG=FE时，不存在． 7.解：(1)∵抛物线上A、B、C三点坐标代入抛物线解析式y＝ax2＋bx＋c得，，解得，∴抛物线的解析式为y＝﹣x2＋3x＋4. (2)结论：△BEP为等腰直角三角形，理由如下：∵点P(2，n)在此抛物线上，∴n＝﹣4＋6＋4＝6，∴P点坐标为(2，6).设直线AP解析式为y＝kx＋b，把A、P两点坐标代入可得，解得，，∴直线AP的解析式为y＝2x＋2，(令x＝0可得y＝2，则E点坐标为(0，2).∵B(4，0)，P(2，6)，∴BP＝2，BE＝2，EP＝2，∴BE2＋EP2＝20＋20＝40＝BP2，且BE＝EP，∴△BEP为等腰直角三角形.   (3)存在.∵y＝﹣x2＋3x＋4＝﹣(x﹣)2＋，∴顶点的坐标为(，)，∵OB＝OC＝4，∴BC＝4，∠ABC＝45°.   以下分两种情况：①若BQ＝DQ，BQ1⊥DQ1，∠BDQ＝45°，如图，过点Q1作Q1M⊥OB，垂足为M，∵BQ1＝DQ1，BD＝4﹣＝，∴BM＝Q1M＝，OM＝4﹣＝，∴Q1的坐标为Q1(，).    ②若DQ2＝BD＝，DQ2⊥BD，易得BC所在的直线解析式为y＝﹣x＋4，代入x＝，得y＝﹣＋4＝，∴DQ2＝BD＝，∴△BDQ2是等腰直角三角形，所以Q2的坐标为Q2(，)，综上所述，Q的坐标为Q1(，)或Q2(，).8.解：(1)依题意得：，解得：，∴抛物线的解析式为y＝x2﹣x﹣3；(2)设直线BC的解析式为y＝kx＋m，∴，解得：，∴y＝x﹣3．设P点坐标为(n，n2﹣n﹣3)，N点的坐标为(n，n﹣3)，∴PN＝﹣n2﹣n，∵PM⊥BC，PD⊥AB，∴∠PMN＝∠PDB，∵∠PNM＝∠BND，∴∠MPN＝∠OBC，∵OB＝4，OC＝3，∴BC＝5，∴PM＝PNcos∠MPN＝PNcos∠OBC＝PN，∴PM＋PN＝PN＝﹣n＝﹣．即当n＝2时，PM＋PN的值最大，此时P点坐标为(2，﹣3)．(3)过点P作PK⊥y轴于K，交抛物线的对称轴于G，如图，∵四边形PEFC为正方形，∴PE＝PC，∠EPC＝90°∵∠PGE＝∠PKC＝90°，∴∠PEG＝∠CPK，∴△PEG≌△CPK(AAS)，∴CK＝PG，设P(x，x2﹣x﹣3)，抛物线的对称轴为直线x＝1，则G(1，x2﹣x﹣3)，K(0，x2﹣x﹣3)，∴PG＝|1﹣x|，CK＝|x2﹣x﹣3＋3|＝|x2﹣x|，∴|1﹣x|＝|x2﹣x|，解方程1﹣x＝x2﹣x得，x1＝，x2＝﹣2(舍去)；解方程x﹣1＝x2﹣x得，x1＝，x2＝﹣4(舍去)；∴P点坐标为(，﹣)或(，﹣)．