中考数学三轮冲刺《二次函数压轴题》强化练习十五（含答案）

这是一份中考数学三轮冲刺《二次函数压轴题》强化练习十五（含答案），共14页。
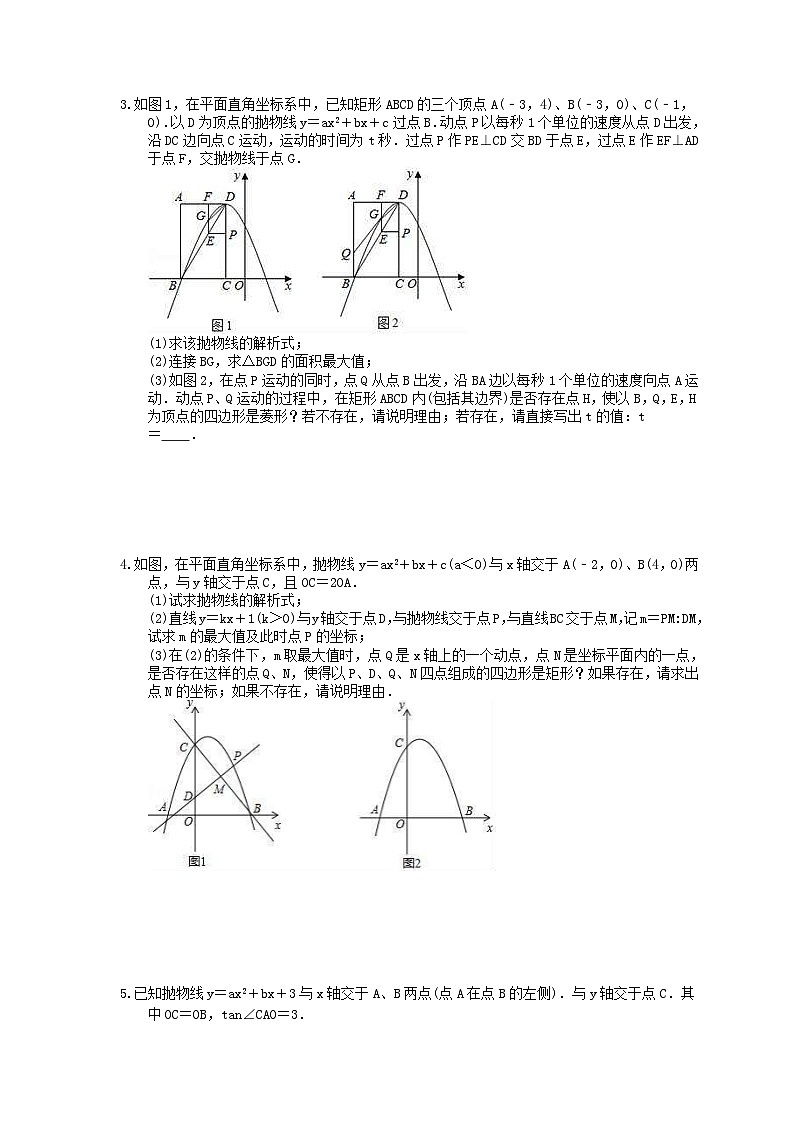
中考数学三轮冲刺《二次函数压轴题》强化练习十五1.有一组邻边相等的凸四边形叫做“和睦四边形”，如菱形，正方形等都是“和睦四边形”．(1)如图1，BD平分∠ABC，AD∥BC，求证：四边形ABCD为“和睦四边形”；(2)如图2，直线AB与x轴，y轴分别交于A(12，0)，B(0，9)两点，点P、Q分别是线段OA、AB上的动点．点P从点A出发，以每秒4个单位长度的速度向点O运动．点Q从点A出发，以每秒5个单位长度的速度向点B运动．P，Q两点同时出发，设运动时间为t秒，当四边形BOPQ为“和睦四边形”时，求t的值；(3)如图3，抛物线y＝ax2＋x＋2(a<0)与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，抛物线的顶点为点D．当四边形COBD为“和睦四边形”，且CD＝OC，求a的值．      2.如图，已知二次函数y=ax2＋bx＋c(a≠0)图象经过点A(1，0)，B(2，0)，C(0，﹣2)，直线x=m(m＞2)与x轴交于点D．(1)求二次函数的解析式；(2)在直线x=m(m＞2)上有一点E(点E在第四象限)，使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似，求E点坐标(用含m的代数式表示)；(3)在(2)成立的条件下，抛物线上是否存在一点F，使得四边形ABEF为平行四边形？若存在，请求出F点的坐标；若不存在，请说明理由．      3.如图1，在平面直角坐标系中，已知矩形ABCD的三个顶点A(﹣3，4)、B(﹣3，0)、C(﹣1，0)．以D为顶点的抛物线y＝ax2＋bx＋c过点B．动点P以每秒1个单位的速度从点D出发，沿DC边向点C运动，运动的时间为t秒．过点P作PE⊥CD交BD于点E，过点E作EF⊥AD于点F，交抛物线于点G．(1)求该抛物线的解析式；(2)连接BG，求△BGD的面积最大值；(3)如图2，在点P运动的同时，点Q从点B出发，沿BA边以每秒1个单位的速度向点A运动．动点P、Q运动的过程中，在矩形ABCD内(包括其边界)是否存在点H，使以B，Q，E，H为顶点的四边形是菱形？若不存在，请说明理由；若存在，请直接写出t的值：t＝　　．      4.如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c(a＜0)与x轴交于A(﹣2，0)、B(4，0)两点，与y轴交于点C，且OC＝2OA．(1)试求抛物线的解析式；(2)直线y＝kx＋1(k＞0)与y轴交于点D，与抛物线交于点P，与直线BC交于点M，记m＝PM:DM，试求m的最大值及此时点P的坐标；(3)在(2)的条件下，m取最大值时，点Q是x轴上的一个动点，点N是坐标平面内的一点，是否存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形？如果存在，请求出点N的坐标；如果不存在，请说明理由．      5.已知抛物线y＝ax2＋bx＋3与x轴交于A、B两点(点A在点B的左侧)．与y轴交于点C．其中OC＝OB，tan∠CAO＝3．(1)求抛物线的解析式；(2)P是第一象限内的抛物线上一动点，Q为线段PB的中点，求△CPQ面积的最大值时P点坐标：(3)将抛物线沿射线CB方向平移2个单位得新抛物线y'．M为新抛物线y′的顶点．D为新抛物线y'上任意一点，N为x轴上一点．当以M、N、C、D为顶点的四边形是平行四边形时，直接写出所有符合条件的点N的坐标．并选择一个你喜欢的N点．写出求解过程．      6.如图，在平面直角坐标系中，抛物线y=x2＋与y轴相交于点A，点B与点O关于点A对称.(1)点B的坐标为        .(2)过点B的直线y=kx＋b(k＜0)与x轴相交于点C，过点C作直线l平行于y轴，P是直线l上一点，且PB=PC，求线段PB的长(用含k的式子表示)，并判断点P是否在抛物线上.(3)在(2)的条件下，若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上，求此时点P的坐标.       7.如图，在平面直角坐标系中，直线y=﹣x+2与x轴交于点A，与y轴交于点B，抛物线y=﹣x2+bx+c经过A，B两点且与x轴的负半轴交于点C．(1)求该抛物线的解析式；(2)若点D为直线AB上方抛物线上的一个动点，当∠ABD=2∠BAC时，求点D的坐标；(3)已知E，F分别是直线AB和抛物线上的动点，当B，O，E，F为顶点的四边形是平行四边形时，直接写出所有符合条件的E点的坐标．      8.如图，在平面直角坐标系中，已知抛物线y＝ax2＋4x＋c与直线AB相交于点A(0，1)和点B(3，4)．(1)求该抛物线的解析式；(2)设C为直线AB上方的抛物线上一点，连接AC，BC，以AC，BC为邻边作平行四边形ACBP，求四边形ACBP面积的最大值；(3)将该抛物线向左平移2个单位长度得到抛物线y=a1x2＋b1x＋c1(a1≠0)，平移后的抛物线与原抛物线相交于点D，是否存在点E使得△ADE是以AD为腰的等腰直角三角形？若存在，直接写出点E的坐标；若不存在，请说明理由．      
0.中考数学三轮冲刺《二次函数压轴题》强化练习十五（含答案）答案解析  一         、综合题1. (1)证明：∵BD平分∠ABC∴∠ABD＝∠CBD，∵AD∥BC，∴∠ADB＝∠CBD，∴∠ABD＝∠ADB，∴AB＝AD，∴四边形ABCD为“和睦四边形”；(2)解：∵A(12，0)，B(0，9)，∴OB＝9，OA＝12，∴AB＝15，由题意得：AQ＝5t，AP＝4t，BQ＝15﹣5t，OP＝12﹣4t，连接PQ，，，∴，又∵∠BAO＝∠QAP，∴△AQP∽△ABO，∴∠APQ＝∠AOB＝90°，∴QP＝3t，∵四边形BOPQ为“和睦四边形”，①当OB＝OP时，9＝12﹣4t，∴；②当OB＝BQ时，9＝15﹣5t，∴；③当OP＝PQ时，12﹣4t＝3t，∴；④当BQ＝PQ时，15﹣5t＝3t，∴，综上所述，t的值为或或或；(3)解：由题意可得：顶点D的坐标为，C(0，2)，∵CD＝OC，∴CD2＝OC2，∴，化简得：，∵a＜0，∴a=﹣． 2.解：(1)将点A(1，0)，B(2，0)，C(0，﹣2)代入二次函数y=ax2＋bx＋c中，得  解得a=﹣1，b=3，c=﹣2．∴y=﹣x2＋3x﹣2．(2)∵AO=1，CO=2，BD=m﹣2，当△EDB∽△AOC时，得=，即=，解得ED=，∵点E在第四象限，∴E1(m，)，当△BDE∽△AOC时， =时，即=，解得ED=2m﹣4，∵点E在第四象限，∴E2(m，4﹣2m)；(3)假设抛物线上存在一点F，使得四边形ABEF为平行四边形，则EF=AB=1，点F的横坐标为m﹣1，当点E1的坐标为(m，)时，点F1的坐标为(m﹣1，)，∵点F1在抛物线的图象上，∴=﹣(m﹣1)2＋3(m﹣1)﹣2，∴2m2﹣11m＋14=0，∴(2m﹣7)(m﹣2)=0，∴m=，m=2(舍去)，∴F1(，﹣)，当点E2的坐标为(m，4﹣2m)时，点F2的坐标为(m﹣1，4﹣2m)，∵点F2在抛物线的图象上，∴4﹣2m=﹣(m﹣1)2＋3(m﹣1)﹣2，∴m2﹣7m＋10=0，∴(m﹣2)(m﹣5)=0，∴m=2(舍去)，m=5，∴F2(4，﹣6)． 3.解：(1)∵矩形ABCD的三个顶点的坐标分别为A(﹣3，4)、B(﹣3，0)、C(﹣1，0)，∴D(﹣1，4)，由抛物线的顶点为D(﹣1，4)，设抛物线的解析式为y＝a(x＋1)2＋4，∵抛物线经过点B(﹣3，0)，∴4a＋4＝0，解得a＝﹣1，∴该抛物线的解析式为y＝﹣(x＋1)2＋4，即y＝﹣x2﹣2x＋3；(2)如图1，设直线BD的解析式为y＝kx＋d，则，解得，∴y＝2x＋6，设G(x，﹣x2﹣2x＋3)(﹣3＜x＜﹣1)，则E(x，2x＋6)，∴GE＝﹣x2﹣2x＋3﹣(2x＋6)＝﹣x2﹣4x﹣3，∵AD＝﹣1﹣(﹣3)＝2，∴S△BGD＝GEAF＋GEDF＝GEAD＝×2(﹣x2﹣4x﹣3)＝﹣(x＋2)2＋1，∴当x＝﹣2时，S△BGD最大＝1，∴△BGD面积的最大值为1．(3)存在．如图2，菱形BQHE以BE为一边.由题意，得BQ＝PD＝EF＝t，∵PQ∥EF，∴四边形BQFE是平行四边形，∴当BQ＝QF＝t时，四边形BQFE是菱形，此时点H与点F重合．∵QF∥BD，∴∠AQF＝∠QBD，∵AD＝2，AB＝4，∠A＝90°，∴BD＝2．∴，∴AQ＝QF＝t，∴t＋t＝4，解得t＝20-8；如图3，菱形BQEH以BE为对角线，连结QH交BE于点R，则QH⊥BE，BR＝ER，∴∠BRQ＝90°，∴，∴BR＝t；同理，，∴DE＝PD＝t，∴2×t＋t＝2，解得t＝．综上所述，t＝20-8或t＝．故答案为：20-8或． 4.解：(1)因为抛物线y＝ax2＋bx＋c经过A(﹣2，0)、B(4，0)两点，所以可以假设y＝a(x＋2)(x﹣4)，∵OC＝2OA，OA＝2，∴C(0，4)，代入抛物线的解析式得到a＝﹣，∴y＝﹣(x＋2)(x﹣4)或y＝﹣x2＋x＋4或y＝﹣(x﹣1)2＋．(2)如图1中，由题意，点P在y轴的右侧，作PE⊥x轴于E，交BC于F．∵CD∥PE，∴△CMD∽△FMP，∴m＝＝，∵直线y＝kx＋1(k＞0)与y轴交于点D，则D(0，1)，∵BC的解析式为y＝﹣x＋4，设P(n，﹣n2＋n＋4)，则F(n，﹣n＋4)，∴PF＝﹣n2＋n＋4﹣(﹣n＋4)＝﹣(n﹣2)2＋2，∴m＝﹣ (n﹣2)2＋，∵﹣＜0，∴当n＝2时，m有最大值，最大值为，此时P(2，4)．(3)存在这样的点Q、N，使得以P、D、Q、N四点组成的四边形是矩形．①当DP是矩形的边时，有两种情形，a、如图中，四边形DQNP是矩形时，有(2)可知P(2，4)，代入y＝kx＋1中，得到k＝，∴直线DP的解析式为y＝x＋1，可得D(0，1)，E(﹣，0)，由△DOE∽△QOD可得＝，∴OD2＝OEOQ，∴1＝OQ，∴OQ＝，∴Q(，0)．根据矩形的性质，将点P向右平移个单位，向下平移1个单位得到点N，∴N(2＋，4﹣1)，即N(，3)b、如图2﹣2中，四边形PDNQ是矩形时，∵直线PD的解析式为y＝x＋1，PQ⊥PD，∴直线PQ的解析式为y＝﹣x＋，∴Q(8，0)，根据矩形的性质可知，将点D向右平移6个单位，向下平移4个单位得到点N，∴N(0＋6，1﹣4)，即N(6，﹣3)．②当DP是对角线时，设Q(x，0)，则QD2＝x2＋1，QP2＝(x﹣2)2＋42，PD2＝13，∵Q是直角顶点，∴QD2＋QP2＝PD2，∴x2＋1＋(x﹣2)2＋16＝13，整理得x2﹣2x＋4＝0，方程无解，此种情形不存在，综上所述，满足条件的点N坐标为(，3)或(6，﹣3)． 5.解：(1)∵抛物线解析式为y＝ax2＋bx＋3，令x＝0得y＝3，∴点C坐标为(0，3)，∵OG﹣OB＝3，∴B坐标为(3，0)，∵tan∠CAO＝3，∴＝3，∴OA＝1，∴点A坐标为(﹣1，0)，∴设解析式为y＝a(x＋1)(x﹣3)，代入(0，3)得a＝﹣1，∴y＝﹣(x＋1)(x﹣3)，＝﹣(x2﹣2x﹣3)＝﹣x2＋2x＋3＝﹣(x﹣1)2＋4，∴抛物线解析式为：y＝﹣(x﹣1)2＋4；(2)∵Q为线段PB中点，∴S△CPQ＝S△CPB，当S△CPB面积最大时，△CPQ面积最大．设P坐标(a，﹣a2＋2a＋3)，过点P作PH∥y轴交BC于点H，H坐标为(a，﹣a＋3)，∴PH＝(﹣a2＋2a＋3)﹣(﹣a＋3)＝﹣a2＋2a＋3＋a﹣3＝﹣a2＋3a，S△CPB＝•PH•(xB﹣xC)＝•PH•3＝PH＝(﹣a2＋3a)＝﹣(a2﹣3a＋﹣)＝﹣(a﹣)2＋，当a＝时，即P坐标为(，)时，最大S△CPQ＝S△CPB＝，∴P坐标为(，)；(3)沿CB方向平移2个单位，即向右2个单位，向下2个单位，∴新抛物线解析式为y＝﹣(x﹣3)2＋2，M坐标为(3，2)C坐标为(0，3)，点N坐标设为(n，0)，∵＝，∴＝，∴yD＝1，则1＝﹣(x﹣3)2＋2﹣1＝﹣(x﹣3)2，(x﹣3)2＝1，x﹣3＝±1，∴x＝4或2，∴xD＝4或xD＝2，＝⇒＝，∴xN＝7，或＝，∴xN＝5，∴N坐标为(7，0)或(5，0)，或＝⇒＝，得yD＝﹣1，则﹣1＝﹣(x﹣3)2＋2，(x﹣3)2＝3，x＝±＋3，∴xD＝3﹣或xD＝3＋，即xN＝﹣或，N坐标为(﹣，0)或(，0)． 6.解：(1)∵抛物线y=x2＋与y轴相交于点A，∴点A(0，).∵点B与点O关于点A对称，∴BA=OA=，∴OB=，即点B的坐标为(0，).(2)∵点B的坐标为(0，)，∴直线的函数表达式为y=kx＋.令y=0，得kx＋=0，解得x=﹣，∴OC=﹣.∵PB=PC，∴点P只能在x轴上方.如图①，过点B作BD⊥l于点D，设PB=PC=m.则BD=OC=﹣，CD=OB=.∴PD=PC﹣CD=m﹣.在Rt△PBD中，由勾股定理，得PB2=PD2＋BD2， 即m2=(m﹣)2＋(﹣)2，解得m=＋，∴PC=＋，∴点P的坐标为(﹣，＋).把x=﹣代入y=x2＋，得y=＋，∴点P在抛物线上.(3)如图，连结CC′.∵l∥y轴，∴∠OBC=∠PCB.又∵PB=PC，∴∠PCB=∠PBC，∴∠PBC=∠OBC.∵点C，C′关于BP对称，且点C′在抛物线的对称轴上，即在y轴上，∴∠PBC=∠PBC′，∴∠OBC=∠PBC=∠PBC′=60°.∴∠BCO=30°，△BCP是等边三角形.∵OB=，∴PC=BC=1，∴OC=，∴点P的坐标为(，1). 7.解：(1)在y=﹣x+2中，令y=0，得x=4，令x=0，得y=2∴A(4，0)，B(0，2)把A(4，0)，B(0，2)，代入y=x2+bx+c，得，解得∴抛物线得解析式为y=x2+x+2.(2)如图，过点B作x轴得平行线交抛物线于点E，过点D作BE得垂线，垂足为F∵BE∥x轴，∴∠BAC=∠ABE∵∠ABD=2∠BAC，∴∠ABD=2∠ABE即∠DBE+∠ABE=2∠ABE∴∠DBE=∠ABE∴∠DBE=∠BAC设D点的坐标为(x，x2+x+2)，则BF=x，DF=x2+x∵tan∠DBE=，tan∠BAC=∴=，解得x1=0(舍去)，x2=2当x=2时，x2+x+2=3∴点D的坐标为(2，3)(3)当BO为边时，OB∥EF，OB=EF，设E(m，﹣m+2)，F(m，m2+m+2)EF=|(﹣m+2)﹣(m2+m+2)|=2解得m1=2，m2=2﹣2，m3=2+2当BO为对角线时，OB与EF互相平分，过点O作OF∥AB，直线OFy=x交抛物线于点F(2+2，﹣1﹣)和((2﹣2，﹣1+))求得直线EF解析式为y=﹣x+1或y=x+1.直线EF与AB的交点为E，点E的横坐标为﹣2﹣2或2﹣2.∴E点的坐标为(2，1)或(2﹣2，1+)或(2+2，1﹣)或(﹣2﹣2，3+)或(﹣2+2，3﹣). 8.解：(1)将A、B两点代入到解析式中，得，，解得，∴抛物线的解析式为：y＝﹣x2＋4x＋1；(2)设直线AB为：y＝k1x＋1，代入点B，得，3k1＋1＝4，解得k1＝1，∴直线AB为：y＝x＋1，设C(m，﹣m2＋4m＋1)，过C作CM∥y轴交AB于M，如图，则M(m，m＋1)，∴CM＝﹣m2＋4m＋1﹣m﹣1＝﹣m2＋3m，∵四边形ACBP为平行四边形，∴S四边形ACBP＝2S△ABC＝2(S△ACM＋S△BCM)＝2×CM×3＝4CM＝3(﹣m2＋3m)＝﹣3(m﹣)2＋，∵﹣3＜0，∴m＝时，四边形ACBP面积的最大值为；(3)∵抛物线y＝﹣x2＋4x＋1＝﹣(x﹣2)2＋5，∴将抛物线向左平移2个单位后得到的抛物线为：y＝﹣x2＋5，联立，解得，∴D(1，4)，①如图，当DA＝DE，∠EDA＝90°，E在AD右侧时，过D作x轴平行线交y轴于N，过E作y轴平行线，两线交于F点，∵∠DAN＋∠NDA＝∠NDA＋∠EDF＝90∴∠DAN＝∠EDF，又∠DNA＝∠EFD＝90°，DA＝DE，∴△DNA≌△EFD(AAS)，∴DN＝EF＝1，AN＝DF＝3，∴E(4，3)，②当DA＝DE，∠EDA＝90°，E在AD左侧，同理可得，E(﹣2，5)，③当AD＝AE，∠DAE＝90°，E在AD左侧时，同理可得，E(﹣3，2)，④当AD＝AE，∠DAE＝90°，E在AD右侧时，同理可得，E(3，0)，综上所述，E(4，3)或(﹣2，5)或(﹣3，2)或(3，0)．