中职物理高教版（2021）通用类主题一 运动和力第五节 牛顿运动定律及其应用教学设计

这是一份中职物理高教版（2021）通用类主题一 运动和力第五节 牛顿运动定律及其应用教学设计，共14页。
          2、空间任意力系的平衡方程及常见的空间约束
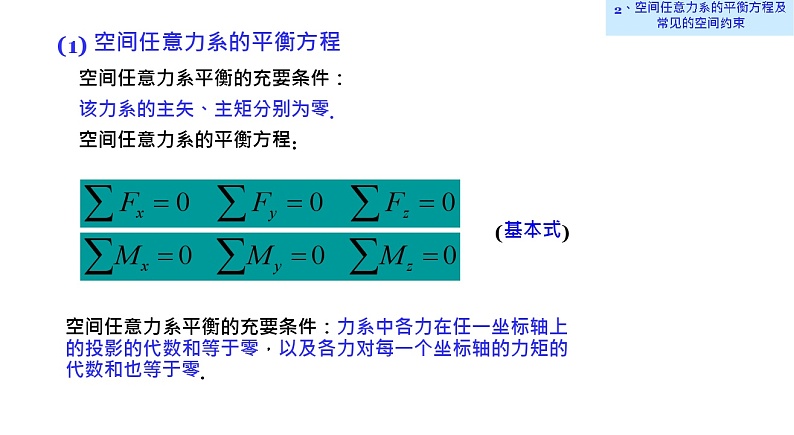
  (1)     空间任意力系的平衡方程空间任意力系平衡的充要条件： 该力系的主矢、主矩分别为零. 空间任意力系的平衡方程:      (基本式)       空间任意力系平衡的充要条件：力系中各力在任一坐标轴上的投影的代数和等于零，以及各力对每一个坐标轴的力矩的代数和也等于零.
        空间任意力系的平衡方程(基本式)  平衡方程除了基本式之外，还有四矩式、五矩式、六矩式。有几个力矩平衡方程，称之为几矩式。 基本式以外的方程形式，通常不再给限定条件，一般的情况下只要列出的方程能求解出未知量即是未违反限制条件。各种形式应该根据实际情况灵活运用。
   空间平行力系的平衡方程            
Fz   0
Mx   0
My   0
    三个方程，能求解三个独立的未知量。
  各种力系的独立平衡方程个数 空间任意力系6个最一般情形：空间、任意空间汇交力系空间平行力系3个3个一级特殊情形（包含一种特殊情况）：空间问题+空间力偶系平面任意力系3个3个特殊力系，或者任意力系+平面情形平面汇交力系平面平行力系平面力偶系2个2个2(1)个二级特殊情形（包含两种特殊情况）：平面问题+ 特殊力系。
  (2)     空间常见约束类型1个未知约束量          二力杆
  2个未知约束量 
径向轴承
蝶铰链
  3个未知约束量
  4个未知约束量    导向轴承 万向接头

  5个未知约束量带有销子的夹板 导轨

   6个未知约束量  空间固定端约束 分析实际的约束时，需要忽略一些次要因素，抓住主要因素，做一些合理   的简化。比如导向轴承和径向轴承之间的区别；蝶铰链和止推轴承之间的   区别。如果刚体只受平面力系的作用，则垂直于该平面的约束力和绕平面   内两轴转动的约束力偶都应该为零，相应减少了约束量的数目。
 例1 车床主轴如图所示，已知车刀对工件的切削力为：径向切削力Fx=4.25kN纵向切削力Fy=6.8kN，主切削力(切向)Fz=17kN，方向如图。在直齿轮C上有切向力Ft和径向力Fr，且Fr=0.36Ft。齿轮C的节圆半径R=50mm，被切削工件的半径r=30mm,卡盘及工件等自重不计，其余尺寸如图所示。当主轴匀速转   动时。求：(1) 齿轮啮合力Ft及Fr；(2) 径向轴承A和止推轴承B的约束力；(3) 三爪卡盘E在O处对工件的约束力。解: (1) 取主轴及工件组成的整体为研究对象，
分析受力。
在Axyz坐标系下，列平衡方程：
F  0 F  F  F
 F  0 F
 x Bx t
Ax x B y
Fy   0 FBy  Fy   0Fz  0 FBz Fr FAz Fz  0
Mx F  0My F  0
 (488  76)FBz  76FrFt  R Fz r  0
 388Fz  0
 z  r Fz
 Mz F   0
(488  76)FBx   76Ft
 388Fx  30Fy  0
Fx x
又： Fr
 0.36Ft ,
R FtFr
左视图（从左往右看）
空间任意力系及重心的计算 
 (2) 取工件为研究对象，建立Oxyz坐标系，分析受力。
Fx   0
FOx
   Fx  0
z100
Fy   0
FOy  Fy  0
FO z FzzO F
 30Fx y
Fz   0
FOz
   Fz  0
MxyFO x
O y  Fy D
 M x F   0
100FZ
   Mx  0 x
 M y F   0
   30FZ
    M y  0
 Mz F   0
100Fx
  30Fy
   Mz  0
FOx
 4.25kN, FOy
 6.8kN, FOz
 17kN
 
 Mx
 1.7kN  m, M y
 0.51kN m, Mz
 0.22kN  m
 空间任意力系有6个独立的平衡方程，可求解6个未知量，但其平衡方程不局限于本例的形式。为了使解题简便，每个方程中最好只包含一个未知量。为此，选投影轴时应尽量与其余未知力垂直；选取矩轴时应尽量与其余的未知力平行或相交。投影轴不必相互垂直，
取矩轴也不必与投影轴重合，力矩方程的数目可取3个至6个。
空间任意力系及重心的计算 
 例2 已知均质水平长方板重为P,用六根无重直杆支承，直杆两端各用球铰链与板和地面连接，板长宽分别为b，a，离地面高度为b. A点作用水平力F=2P，求各根杆的受力。z解：取均质板为研究对象，各杆均为二力杆，编号 b如图。假设杆都受拉力，分析板的受力。
 M AB (F )  0
    F6
 a  P  a  0
a D          CF
2 F A
6 bF11 H P F5 6
 M AE (F )  0 M AC (F )  0 MBF (F )  0
 F5    0 F4    0 F1     0
F2 F32 x E
5 G y3 4F
 M (F )  0
Fb  P  b  F 
 b  0
FG 2 2
 M (F )  0
   F  b 
P  b  F 
cos 45  b  0
BC 2 2 3 空间任意力系及重心的计算