新教材2023年高中数学第5章三角函数5.4三角函数图象与性质5.4.2正弦函数余弦函数的性质第2课时正弦函数余弦函数的性质二课件新人教A版必修第一册

这是一份新教材2023年高中数学第5章三角函数5.4三角函数图象与性质5.4.2正弦函数余弦函数的性质第2课时正弦函数余弦函数的性质二课件新人教A版必修第一册，共52页。

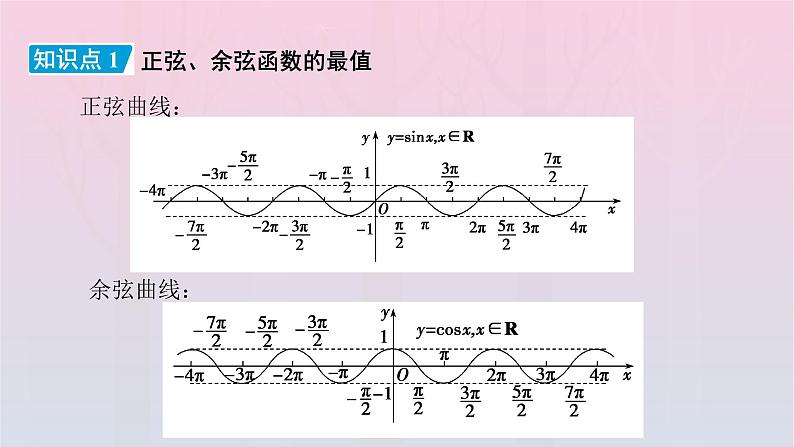
第五章　三角函数5.4　三角函数图象与性质5.4.2　正弦函数、余弦函数的性质第2课时　正弦函数、余弦函数的性质(二)必备知识 · 探新知正弦曲线：知识点 1正弦、余弦函数的最值余弦曲线：定义域　值域　想一想：(1)正、余弦函数的定义域、值域各是什么？(2)从图象的变化趋势来看，正弦、余弦函数的最大值、最小值点分别处在什么位置？提示：(1)正弦、余弦函数的定义域为R，值域为[－1，1]．(2)正弦、余弦函数的最大值、最小值均处于图形拐弯的地方．练一练：1．函数y＝2－sin x取得最大值时x的值为_________________．2．函数y＝cos x的最大值为___，最小值为_____．1　－1　知识点 2正弦、余弦函数的单调性提示：(1)观察图象可知：(2)观察图象可知：当x∈[－π，0]时，曲线逐渐上升，是增函数，cos x的值由－1增大到1；当x∈[0，π]时，曲线逐渐下降，是减函数，cos x的值由1减小到－1.推广到整个定义域可得当x∈[2kπ－π，2kπ]，k∈Z时，余弦函数y＝cos x是增函数，函数值由－1增大到1；当x∈[2kπ，(2k＋1)π]，k∈Z时，余弦函数y＝cos x是减函数，函数值由1减小到－1.C　D　关键能力 · 攻重难典例1[归纳提升]　单调区间的求法求形如y＝Asin(ωx＋φ)或y＝Acos(ωx＋φ)的函数的单调区间，要先把ω化为正数，(1)当A>0时，把ωx＋φ整体代入y＝sin x或y＝cos x的单调递增区间内，求得的x的范围即为函数的单调递增区间．(2)当A<0时，把ωx＋φ整体代入y＝sin x或y＝cos x的单调递增区间内，求得的x的范围即为函数的单调递减区间；代入y＝sin x或y＝cos x的单调递减区间内，可求得函数的单调递增区间．提醒：求函数y＝Asin(ωx＋φ)的单调区间时，把ωx＋φ看作一个整体，借助y＝sin x的单调区间来解决．当A<0或ω<0时，要注意原函数的单调性与y＝sin x的单调性的关系．典例2【对点练习】❷ (1)已知α，β为锐角三角形的两个内角，则以下结论正确的是 (　　)A．sin αcos β(2)将cos 150°，sin 470°，cos 760°按从小到大排列为__________________________________________．B　cos 150°sin 12°>sin 11°，即cos 10°>sin 168°>sin 11°.C　B　5．函数y＝cos2x－4cos x＋5的值域为___________．[解析]　令t＝cos x，由于x∈R，故－1≤t≤1.y＝t2－4t＋5＝(t－2)2＋1，当t＝－1时，即cos x＝－1时函数有最大值10；当t＝1，即cos x＝1时函数有最小值2.所以该函数的值域是[2，10]．[2，10]