2023年黑龙江省鸡西市虎林市实验中学中考二模数学试题

二〇二三年初中生学业水平考试

数学试题

考生注意：

1．考试时间120分钟

2．全卷共三道大题，总分120分

一、选择题（每题3分，满分30分）

1．下列运算正确的是（    ）

A．3mn-2mn=1 B．（m2n2）2=m4n6 C． D．（m+n）2=m2+n2

2．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（    ）

A． B． C． D．

3．据统计，某班7个学习小组上周参加“青年大学习”的人数分别为：5，5，6，6，6，7，7，下列说法错误的是（    ）

A．该组数据的中位数是6  B．该组数据的众数是6

C．该组数据的平均数是6  D．该组数据的方差是6

4．如图是由几个小正方体组成的几何体，它的左视图是（    ）

A． B． C． D．

5．“新冠肺炎”防治取得战略性成果．若有一个人患了“新冠肺炎”，经过两轮传染后共有16个人患了“新冠肺炎”，则每轮传染中平均一个人传染的人数是（    ）

A．2 B．3 C．4 D．5

6．若关于x的分式方程有正整数解，则整数m为（    ）

A．-3 B．0 C．-1 D．-1或0

7．2022年新冠肺炎疫情比较严重，爸爸给小亮50元钱让他购买两种口罩：N95口罩和医用口罩（两种都买），医用口罩2元一个，N95口罩5元一个，在把钱用尽的条件下，不同的买法有（    ）

A．2种 B．3种 C．4种 D．5种

8．如图，在平面直角坐标系中，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点8在y轴正半轴上，反比例函数（k≠0，>0）的图象同时经过顶点C，D．若点C的横坐标为6，BE=3DE，则k的值为（    ）

A． B．3 C． D．6

9．如图，在菱形ABCD中，对角线AC，BD交于点O，其中OA=1．OB=2，则菱形ABCD的面积为（    ）

A．4 B．6 C．8 D．12

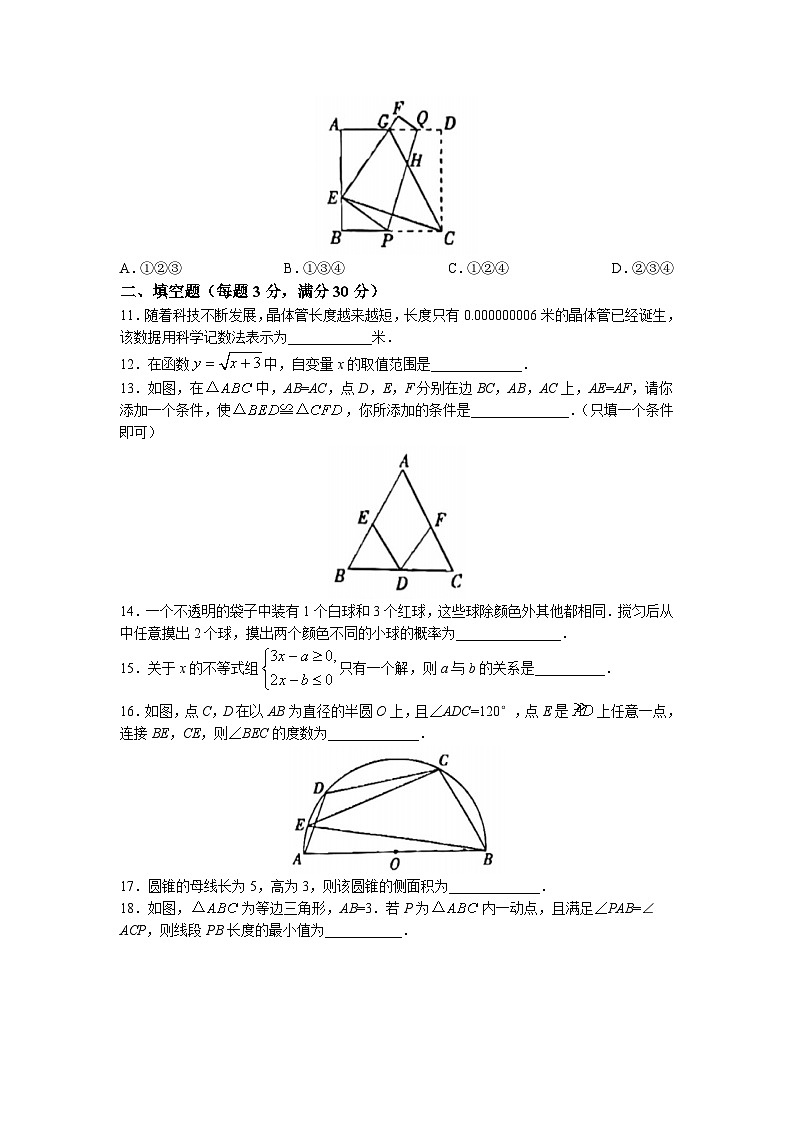
10．如图，将正方形纸片ABCD沿PQ折叠，使点C的对称点E落在边AB上，点D的对称点为点F，EF为交AD于点G，连接CG交PQ于点H，连接CE．下列四个结论中：①；②；③EC平分∠BEG；④，正确的是（    ）

A．①②③ B．①③④ C．①②④ D．②③④

二、填空题（每题3分，满分30分）

11．随着科技不断发展，晶体管长度越来越短，长度只有0.000000006米的晶体管已经诞生，该数据用科学记数法表示为____________米．

12．在函数中，自变量x的取值范围是_____________．

13．如图，在中，AB=AC，点D，E，F分别在边BC，AB，AC上，AE=AF，请你添加一个条件，使，你所添加的条件是______________．（只填一个条件即可）

14．一个不透明的袋子中装有1个白球和3个红球，这些球除颜色外其他都相同．搅匀后从中任意摸出2个球，摸出两个颜色不同的小球的概率为_______________．

15．关于x的不等式组只有一个解，则a与b的关系是__________．

16．如图，点C，D在以AB为直径的半圆O上，且∠ADC=120°，点E是上任意一点，连接BE，CE，则∠BEC的度数为_____________．

17．圆锥的母线长为5，高为3，则该圆锥的侧面积为_____________．

18．如图，为等边三角形，AB=3．若P为内一动点，且满足∠PAB=∠ACP，则线段PB长度的最小值为___________．

19．如图，在平面直角坐标系中，矩形ABOC的边BO，CO分别在x轴、y轴上，点A的坐标为（-8，6），点P在矩形ABOC的内部，点E在BO边上，满足，当是等腰三角形时，点P的坐标为_____________．

20．如图．已知等边的边长为1，作OD⊥AC于点D，在x轴上取点C1，使CC­=DC，以CC1为边作等边；作CD，⊥A，C，于点D，在x轴上取点C2，使C，C2=D，C，

以C，C2为边作等边；作C1D2⊥A2C2于点D2，在x轴上取点C3，使C2C3=D2C2，以C2C3为边作等边……且点A，A1，A2，A3，……都在第一象限，如此下去，则等边的边中点的横坐标为______________．

三、解答题（满分60分）

21．（本题5分）先化简，再求值：，再任选一个你喜欢的数代入求值．

22．（本题6分）如图，在平面直角坐标系中，的顶点坐标分别为A（5，4），B（0，3），C（2，1）．

（1）画出关于原点对称的，并写出点C1的坐标；

（2）画出将绕点C1按顺时针方向旋转90°所得的；

（3）计算（2）中点A1旋转到，点A2所经过的路径长．

23．（本题6分）如图，抛物线y=ax2+2ax+c与x轴交于点A，B，交y轴于点C（0，-3），且AB=4，请解答下列问题：

（1）求抛物线的解析式；

（2）过，点B的直线把的面积分成1∶2两部分，且交抛物线y=ax2+2ax+c的对称轴于点P，则点P的坐标为___________．

24．（本题7分）为促进体育教育，提高学生身体素质，某校针对学生对体育知识的了解程度进行了一次抽样调查统计，并将数据分为A．不了解；B．一般了解；C．了解较多；D．熟悉四组．根据收集的数据，绘制了如下两幅不完整的统计图．请你根据图中提供的信息回答以下问题：

（1）这次被调查的学生共有多少名？

（2）补全条形统计图；

（3）求出扇形统计图中“了解较多”部分所对应的圆心角度数；

（4）该中学初中共有1200名学生，估计对体育知识了解程度为“熟悉”的学生大约有多少．

25．（本题8分）甲、乙两车同时从A地出发，匀速开往B地，甲车行驶到B地后立即沿原路线以原速度返回A地，到达A地后停止行驶．当甲车到达A地时，乙车恰好到达B地，并停止行驶．已知甲车的速度为150km/h，设甲车出发的时间为x（单位：h），甲、乙两车之间的距离为y（单位：km），图中的折线OMNQ表示整个运动过程中y与x之间的函数关系．

（1）A，B两地之间距离是____________km，乙车的速度是____________km/h；

（2）求线段MN的函数表达式（不需写出自变量的取值范围），并指出点M的实际意义；

（3）直接写出甲车出发多长时间，两车相距50km．

26．（本题8分）已知和中，AB=AC，AD=AE，∠BAC=∠DAE=90°，连接CE，G，F分别是BC，DE的中点，连接FG．

（1）如图1，当点D在内部时，求证；

（2）如图2、图3，当点D在外部时，请直接写出EC与FG的数量关系，不需要证明．

27．（本题10分）某公司生产的一种营养品信息如表．已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克．

（1）甲、乙两种食材每千克进价分别是多少元？

（2）该公司每日用18000元购进甲、乙两种食材并恰好全部用完，则每日购进甲、乙两种食材各多少千克？

（3）在（2）的条件下，已知每日其他费用为2000元，且生产的营养品当日全部售出．若A包装的数量不低于B包装的数量，则当A包装为多少包时，每日所获总利润最大？最大总利润为多少元？

28．（本题10分）如图所示，直线AB与y轴x轴交于点A、点B，且OA，OB的长分别为方程x2-12x+32=0的两个根（OA<OB）．点C在y轴上，且OA∶AC=2∶5，直线CD垂直直线AB于点P，交x轴于点D．

（1）求点A、点B的坐标；

（2）点Q在线段CD上从点C向点D匀速运动，运动速度为每秒1个单位长度，设点Q的运动时间为t秒，的面积为S，请求出S和t之间的函数关系式并注明自变量的取值范围；

（3）在（2）的条件下，是否存在点Q，使和相似？若存在，直接写出点Q的坐标；若不存在，请说明理由．

参考答案

一、选择题

1．B  2．A  3．D  4．A  5．B  6．D  7．C  8．C  9．A  10．B

二、填空题

1．6×10-9   12．x≥-3（写x>-3不给分）   13．BD=CD（答案不唯一）   14．

15．2a=3b   16．30°   17．20π   18．   19．或（-4，3）   20．

三、解答题

21．解：原式=且．

当a=10时，原式．

22．解：（1）如图所示．点C1的坐标为（-2，-1）．

（2）如图所示．

（3）．

点A1旋转到点A2所经过的路径长为．

23．解：（1）∵抛物线的对称轴为，，

∴抛物线经过点，．

∴解得  ∴抛物线的解析式为．

（2）．或．

24．解：（1）调查的学生为5÷10%=50（名）．

（2）“一般了解”的学生有50×30%=15（名），

“熟悉”的学生有50-5-15-20=10（名）．

补全条形统计图如图．

（3）“了解较多”部分所对应的圆心角度数为．

（4）（名）．

25．解：（1）A、B两地的距离是150×4=600（km），乙车的速度为150÷2=75（km/h）．

（2）8÷2=4（h）．（150-75）×4=300（km）．∴M（4，300）．

，∴．

设线段MN的函数表达式为y=kx+b．

∴  解得

∴线段MN的函数表达式为y=-225x+1200．

点M的实际意义是在两车行驶4h时，甲车到达B地，此时甲、乙两车的距离是300km．

（3）∵当0≤x≤4时．（150-75）x=50，解得；

当时，（150+75）x+50=600×2，解得；

当时，（150+75）x-50=600×2，解得．

∴当两车相距50km时，甲车出发或或．

26．（1）如图1，连接AF，AG．

∵AB=AC，AD=AE，∠BAC=∠DAE=90°，

∴和均是等腰直角三角形．

∵G，F分别为BC，DE的中点，

∴∠GAC=∠FAE=45°，，．

∴∠CAE=∠CAF，．

∴，∴．∴．

（2）图2：．

（3）图3：．

27．（1）解：设乙食材每千克进价为a元，则甲食材每千克进价为2a元．

由题意，得．

解得a=20．经检验a=20是分式方程的根，且符合题意．

∴2×20=40（元）．

（2）设每日购进甲食材x千克，乙食材y千克．

由题意，得

解得

（3）设A包装为m包，则B包装为包．

∵A包装的数量不低于B包装的数量，

∴m≥2000-4m．∴m≥400．

设总利润为W元．根据题意，得W=45m+12（2000-4m）-18000-2000=-3m+4000．

∵k=-3<0，∴W随m的增大而减小．

∴当m=400时，W的最大值为2800．

28．解：（1）∵x2-12x+32=0，∴x1=4，x2=8．∵OA<OB，∴点A（0，4），B（-8，0）．

（2）∵OA=4，OA∶AC=2∶5，∴AC=10．∴OC=4+10=14．∴点C（0，14）．

∵CD⊥BP，∴∠CPB=90°．∴∠OBA=∠OCD．∴．

∴．∴．∴OD=7．

∴D（7，0）．∴．

如图，过点Q作QM⊥OC于点M．

∴．∴．∴．

∴．∴．

∴．

（3）存在．，．