




还剩6页未读,
继续阅读
9.1.2 第2课时 含“≤”“≥”的不等式 新人教版七年级数学下册课件
展开
这是一份9.1.2 第2课时 含“≤”“≥”的不等式 新人教版七年级数学下册课件,共12页。
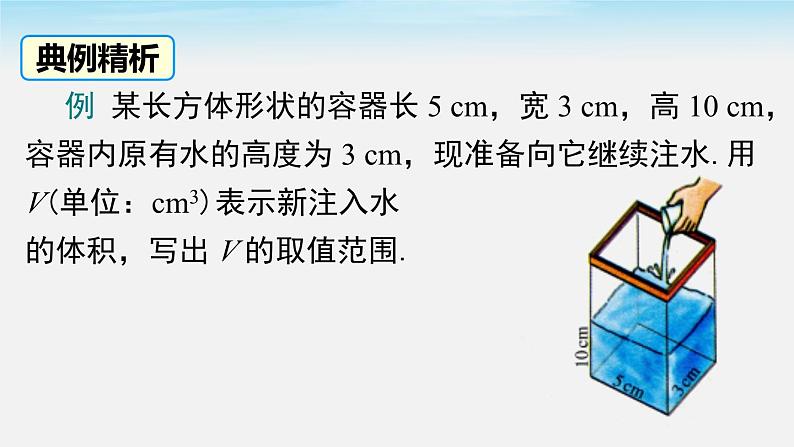
第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质第2课时 含“≤”“≥”的不等式问题 前面学过哪几种形式的不等式?x<a,x>a,x≠a.思考 写出下列图片信息中的含义:回顾与思考问题1 一辆轿车在一条规定车速不低于 60 km/h,且不高于 100 km/h 的高速公路上行驶,如何用式子来表示轿车在该高速公路上正常行驶的路程 s (km)与行驶时间 x (h)之间的不等关系呢?根据路程与速度、时间之间的关系可得:s≥60x,且 s≤100x.含“≤”“≥”的不等式问题2 某运输部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过 160 cm. 设行李的长、宽、高分别为 a cm,b cm,c cm,请你列出行李的长、宽、高满足的关系式. 根据题意可得: a + b + c≤160.<>≥≤>0<0≥0≤0常用的表示不等关系的关键词语及对应的不等号像a≥b或a≤b这样的式子,也经常用来表示两个数量的大小关系. 其中“≥”读作大于或等于,“≤” 读作小于或等于.含“≤”“≥”的不等式 例 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.典例精析解:新注入水的体积 V 与原有水的体积的和不能超过 容器的容积,即V + 3×5×3≤3×5×10,解得 V≤105. 由于新注入水的体积不能是负数,因此,V 的取值范围是 V≥0 并且 V≤105.在数轴上表示 V 的取值范围如图所示.利用不等式的性质解不等式的注意事项2.要注意区分“大于”“不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来;3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点.1.在运用性质 3 时,要特别注意:不等式两边都乘或除以同一个负数时,要改变不等号的方向;1. 用不等式表示下列语句并写出解集,并在数轴上表 示解集.(1)x 的 3 倍大于或等于 1;(2)x 与 3 的和不小于 6;(3)y 与 1 的差不大于 0;(4)y 的 小于或等于 -2. 分析:准确找出本题中表示数量不等关系的关键词语,并正确使用不等号. (1)(2) 中大于或等于、不小于都用“ ≥”表示;(3)(4) 中不大于、小于或等于都用“≤”表示. (2)x+3≥6,解集是 x≥3.(3) y - 1≤0,解集是 y≤1.2. 小鸣就读的学校上午第一节课的上课时间是 8 点. 小鸣家距学校有 2 千米,而他的步行速度为每小时 10 千米. 那么,小鸣上午几点从家里出发才能保证不迟到? 解:设小鸣从家里出发到学校需要 x 小时,根据题意得答:小鸣上午 7:48 前从家里出发才能不迟到.解得一个概念:不等式两种思想:数学建模、类比等式三个注意:一要注意“负数”“非负数”“不大于”“不小于”等关键词语的含义;二要注意仔细审题,正确列出不等式;三要注意观察生活,让数学服务于生活.
第九章 不等式与不等式组9.1 不等式9.1.2 不等式的性质第2课时 含“≤”“≥”的不等式问题 前面学过哪几种形式的不等式?x<a,x>a,x≠a.思考 写出下列图片信息中的含义:回顾与思考问题1 一辆轿车在一条规定车速不低于 60 km/h,且不高于 100 km/h 的高速公路上行驶,如何用式子来表示轿车在该高速公路上正常行驶的路程 s (km)与行驶时间 x (h)之间的不等关系呢?根据路程与速度、时间之间的关系可得:s≥60x,且 s≤100x.含“≤”“≥”的不等式问题2 某运输部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过 160 cm. 设行李的长、宽、高分别为 a cm,b cm,c cm,请你列出行李的长、宽、高满足的关系式. 根据题意可得: a + b + c≤160.<>≥≤>0<0≥0≤0常用的表示不等关系的关键词语及对应的不等号像a≥b或a≤b这样的式子,也经常用来表示两个数量的大小关系. 其中“≥”读作大于或等于,“≤” 读作小于或等于.含“≤”“≥”的不等式 例 某长方体形状的容器长 5 cm,宽 3 cm,高 10 cm,容器内原有水的高度为 3 cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出 V 的取值范围.典例精析解:新注入水的体积 V 与原有水的体积的和不能超过 容器的容积,即V + 3×5×3≤3×5×10,解得 V≤105. 由于新注入水的体积不能是负数,因此,V 的取值范围是 V≥0 并且 V≤105.在数轴上表示 V 的取值范围如图所示.利用不等式的性质解不等式的注意事项2.要注意区分“大于”“不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来;3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点.1.在运用性质 3 时,要特别注意:不等式两边都乘或除以同一个负数时,要改变不等号的方向;1. 用不等式表示下列语句并写出解集,并在数轴上表 示解集.(1)x 的 3 倍大于或等于 1;(2)x 与 3 的和不小于 6;(3)y 与 1 的差不大于 0;(4)y 的 小于或等于 -2. 分析:准确找出本题中表示数量不等关系的关键词语,并正确使用不等号. (1)(2) 中大于或等于、不小于都用“ ≥”表示;(3)(4) 中不大于、小于或等于都用“≤”表示. (2)x+3≥6,解集是 x≥3.(3) y - 1≤0,解集是 y≤1.2. 小鸣就读的学校上午第一节课的上课时间是 8 点. 小鸣家距学校有 2 千米,而他的步行速度为每小时 10 千米. 那么,小鸣上午几点从家里出发才能保证不迟到? 解:设小鸣从家里出发到学校需要 x 小时,根据题意得答:小鸣上午 7:48 前从家里出发才能不迟到.解得一个概念:不等式两种思想:数学建模、类比等式三个注意:一要注意“负数”“非负数”“不大于”“不小于”等关键词语的含义;二要注意仔细审题,正确列出不等式;三要注意观察生活,让数学服务于生活.
相关资料
更多









