
所属成套资源:全国初三数学自主招生专题大揭秘(含答案详解)
专题23 四边形-全国初三数学自主招生专题大揭秘(含答案详解)
展开
这是一份专题23 四边形-全国初三数学自主招生专题大揭秘(含答案详解),共26页。
专题23 四边形
一.选择题(共12小题)
1.(2021•黄州区校级自主招生)如图,在矩形ABCD中,E是BC上的点,F是CD上的点,S△ABE=S△ADF=,则=( )
A.3 B. C.5 D.
2.(2021•浦东新区校级自主招生)小明每走5米,顺时针转20°,则( )
A.小明不会回到原点
B.小明会回到原点,路程小于80m
C.小明会回到原点,路程恰为90m
D.小明会回到原点,路程大于120m
3.(2021•长寿区自主招生)如图,在四边形ABCD中,AC与BD相交于点O,∠BAD=90°,BO=DO,那么添加下列一个条件后,仍不能判定四边形ABCD是矩形的是( )
A.∠ABC=90° B.∠BCD=90° C.AB=CD D.AB∥CD
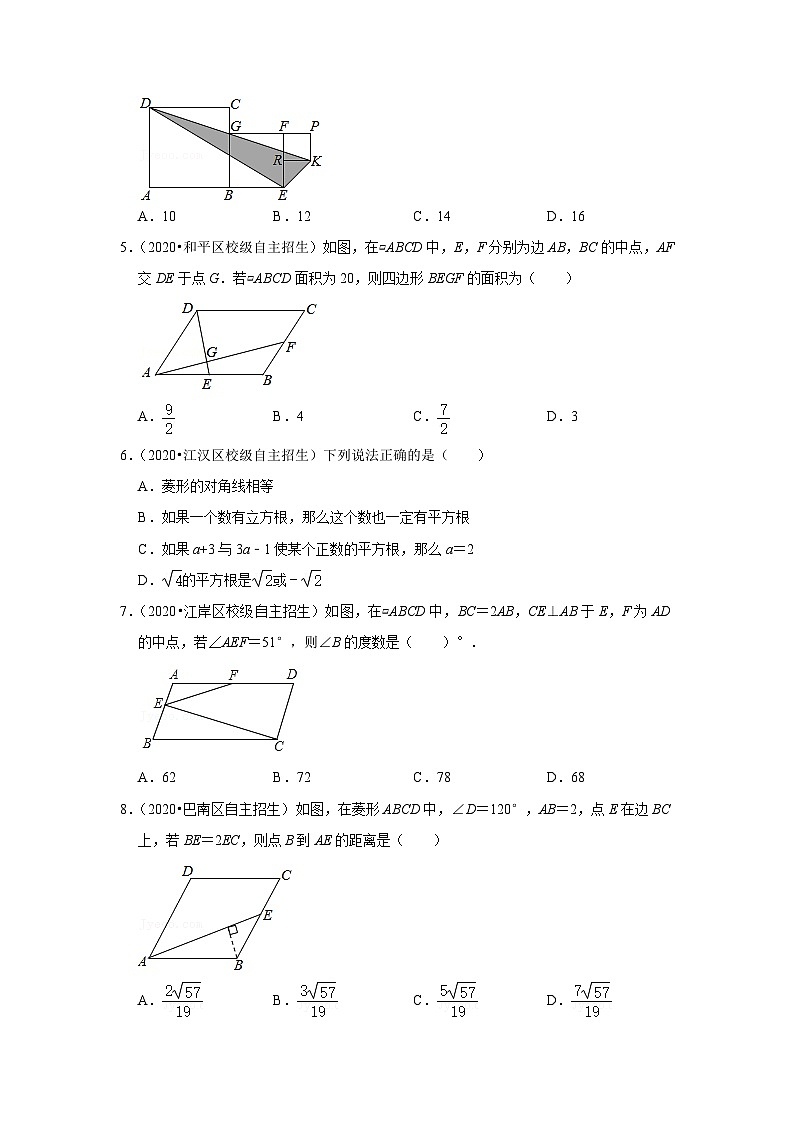
4.(2021•武进区校级自主招生)正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
A.10 B.12 C.14 D.16
5.(2020•和平区校级自主招生)如图,在▱ABCD中,E,F分别为边AB,BC的中点,AF交DE于点G.若▱ABCD面积为20,则四边形BEGF的面积为( )
A. B.4 C. D.3
6.(2020•江汉区校级自主招生)下列说法正确的是( )
A.菱形的对角线相等
B.如果一个数有立方根,那么这个数也一定有平方根
C.如果a+3与3a﹣1使某个正数的平方根,那么a=2
D.的平方根是或﹣
7.(2020•江岸区校级自主招生)如图,在▱ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=51°,则∠B的度数是( )°.
A.62 B.72 C.78 D.68
8.(2020•巴南区自主招生)如图,在菱形ABCD中,∠D=120°,AB=2,点E在边BC上,若BE=2EC,则点B到AE的距离是( )
A. B. C. D.
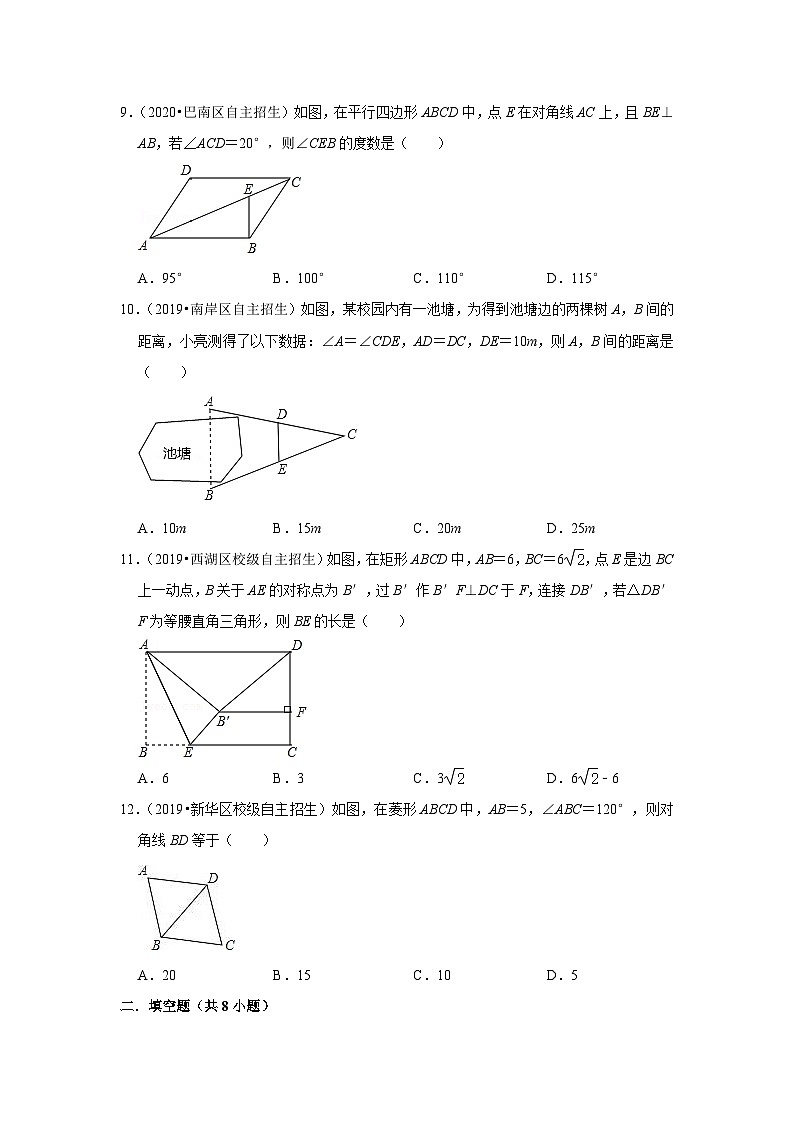
9.(2020•巴南区自主招生)如图,在平行四边形ABCD中,点E在对角线AC上,且BE⊥AB,若∠ACD=20°,则∠CEB的度数是( )
A.95° B.100° C.110° D.115°
10.(2019•南岸区自主招生)如图,某校园内有一池塘,为得到池塘边的两棵树A,B间的距离,小亮测得了以下数据:∠A=∠CDE,AD=DC,DE=10m,则A,B间的距离是( )
A.10m B.15m C.20m D.25m
11.(2019•西湖区校级自主招生)如图,在矩形ABCD中,AB=6,BC=6,点E是边BC上一动点,B关于AE的对称点为B′,过B′作B′F⊥DC于F,连接DB′,若△DB′F为等腰直角三角形,则BE的长是( )
A.6 B.3 C.3 D.6﹣6
12.(2019•新华区校级自主招生)如图,在菱形ABCD中,AB=5,∠ABC=120°,则对角线BD等于( )
A.20 B.15 C.10 D.5
二.填空题(共8小题)
13.(2021•宝山区校级自主招生)已知△ABC,=,=,边BC上有点P1、P2、P3…P22,使得BP1=P1P2=P2P3=…P22C,则+++…+= .
14.(2021•渝中区校级自主招生)如图,矩形ABCO的边OA、OC分别在x轴、y轴上,反比例函数y=交AB、BC于点D、E,BD=2AD,将△BDC沿CD翻折得△FDC,连接EF,若EF∥AB,且EF=4,则k= .
15.(2021•大渡口区自主招生)如图,矩形ABCD中,BC=8,AB=6,点E为CD边上一动点(不与C,D重合).以CE为边向外作矩形CEFG,且CE:CG=3:4,连接BF,点O是线段BF的中点.连接OE,则OE的最小值为 .
16.(2020•和平区校级自主招生)如图,将图(1)中的正六边形进行分割得到图(2),再将图(2)中最小的某一个正六边形按同样的方式进行分割得到图(3),再将图(3)中最小的某一个正六边形按同样的方式进行分割,…,则图(2020)中的正六边形共有 个.
17.(2020•和平区校级自主招生)如图,将正方形ABCD折叠,使A点落在边CD上的点Q
处,且DQ=2CQ,折痕FG交AC于点E,交AD于点F,交BC于点G,则 = .
18.(2020•温江区校级自主招生)如图,Rt△ABC的锐角顶点A,B在直线l上,将直线l向上平移d个单位长度得到直线l',交AC,BC于点D,E,以DE为一边作菱形DEFG,使得顶点F,G在线段AB上,经探究发现,作出菱形的个数与d的大小有关.设AC=3,BC=4,当能作且只能作1个菱形时,d的取值范围为 .
19.(2020•宝山区校级自主招生)直线l1∥l2∥l3∥l4,其中l1,l2之间距离和l3,l4之间距离均为1,l2,l3之间距离为2.正方形ABCD的四个顶点分别在l1,l2,l3,l4上,则S四边形ABCD= .
20.(2020•浙江自主招生)如图,矩形ABCD中分割出①②③三个等腰直角三角形,若已知EF的值,则可确定其中两个三角形的周长之差,这两个三角形的序号是 .
三.解答题(共5小题)
21.(2021•
渝中区校级自主招生)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)如图1,在四边形ABCD中,∠A=60°,∠C=30°,AB=AD,求证:四边形ABCD是勾股四边形;
(2)如图2,在四边形ABCD中,∠DAB=60°,∠DCB=60°,AB=AD,且BC+DC=8,连接AC,求AC的最小值.
22.(2020•渝中区校级自主招生)在平行四边形ABCD中,AC=BC,BE⊥AC分别交直线AC、AD于点E、F.点G是BC上一点,连接EG,过点G作GQ⊥AB分别交BF、AB于点P、Q.
(1)如图1,若AB=AC,BE=3,求AF的长度.
(2)如图2,若PG=2BQ,请探究EG、BG、CG的数量关系,并说明理由.
23.(2020•渝北区自主招生)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AD⊥BD,点E,F,G分别是线段AB,OD,OC的中点,若AD=2,CD=.
(1)求△AOD的面积;
(2)求证:EF∥BG.
24.(2020•九龙坡区自主招生)如图,在平行四边形ABCD中,连接DB.过D点作DE⊥AB于点E,过BE上一点F作FG⊥AD于点G,交DE于点P;过F作FH⊥DB于点H,连接EH.
(1)若DE=6,DC=10,AD=2,求BE的长.
(2)若AE=PE,求证:DH+HF=EH.
25.(2019•永春县校级自主招生)菱形ABCD中,点P为CD上一点,连接BP.
(1)如图1,若BP⊥CD,菱形ABCD边长为10,PD=4,连接AP,求AP的长.
(2)如图2,连接对角线AC、BD相交于点O,点N为BP的中点,过P作PM⊥AC于M,连接ON、MN.试判断△MON的形状,并说明理由.
专题23 四边形
参考答案与试题解析
一.选择题(共12小题)
1.【解答】解:∵S△ABE=S△ADF=,
即BE•AB=AD•DF=AB•BC=AD•CD,
∴BE=BC,DF=DC,
∴EC=BC,CF=CD,
∴S△EFC=×EC×CF=×BC×CD=S矩形ABCD,
∴S△AEF=S矩形ABCD﹣S△ABE﹣S△ADF﹣S△EFC=S矩形ABCD,
∴=3,
故选:A.
2.【解答】解:根据题意可知:组成的多边形的边数360°÷20°=18,
小明走的路程总和是18×5m=90(m),
所以小明会回到原点,路程恰为90m.
故选:C.
3.【解答】解:A、∵∠BAD=90°,BO=DO,
∴OA=OB=OD,
∵∠ABC=90°,
∴AO=OB=OD=OC,
即对角线平分且相等,
∴四边形ABCD为矩形,正确;
B、∵∠BAD=90°,BO=DO,
∴OA=OB=OD,∵∠BCD=90°,
∴AO=OB=OD=OC,
即对角线平分且相等,
∴四边形ABCD为矩形,正确;
C、∵∠BAD=90°,BO=DO,AB=CD,
无法得出△ABO≌△DCO,
故无法得出四边形ABCD是平行四边形,
进而无法得出四边形ABCD是矩形,错误;
D、∵AB||CD,∠BAD=90°,
∴∠ADC=90°,
∵BO=DO,
∴OA=OB=OD,
∴∠DAO=∠ADO,
∴∠BAO=∠ODC,
∵∠AOB=∠DOC,
∴△AOB≌△DOC,
∴AB=CD,
∴四边形ABCD是平行四边形,
∵∠BAD=90°,
∴▱ABCD是矩形,正确;
故选:C.
4.【解答】解:如图,连DB,GE,FK,则DB∥GE∥FK,
在梯形GDBE中,S△DGE=S△GEB(同底等高的两三角形面积相等),
同理S△GKE=S△GFE.
∴S阴影=S△DGE+S△GKE,
=S△GEB+S△GEF,
=S正方形GBEF,
=4×4
=16
故选:D.
5.【解答】解:延长DC,AF交于点M,
∵F为BC的中点,
∴CF=BF,
∵DM∥AB,
∴∠M=∠FAB,
在△ABF和△MCF中,
,
∴△ABF≌△MCF(AAS),
∴AB=CM=CD,
∵E为AB中点,
∴AE=AB=DM,
∵DM∥AB,
∴△AEG∽△MDG,
∵==,
∴S△AEG:S△ADG=1:4,
∵S△ADE=S△ABF=S平行四边形ABCD=5,
∴S△AEG=S△ADG=S△ADE=1,
∴S△ADG+S△AEG=S四边形BEGF+S△AEG,
∴S四边形BEGF=S△ADG=S△ADE﹣S△AEG=5﹣1=4.
故选:B.
6.【解答】解:A、菱形的对角线互相垂直平分,故选项A不符合题意;
B、如果一个数有立方根,那么这个数不一定有平方根,故选项B不符合题意;
C、如果a+3与3a﹣1使某个正数的平方根,那么a=2或a=,故选项C不符合题意;
D、的平方根是或﹣,故选项D符合题意,
故选:D.
7.【解答】解:过F作FG∥AB∥CD,交BC于G;
则四边形ABGF是平行四边形,所以AF=BG,即G是BC的中点;
∵BC=2AB,为AD的中点,
∴BG=AB=FG=AF,
连接EG,
在Rt△BEC中,EG是斜边上的中线,
∴BG=GE=FG=BC;
∵AE∥FG,
∴∠EFG=∠AEF=∠FEG=51°,
∴∠AEG=∠AEF+∠FEG=102°,
∴∠B=∠BEG=180°﹣102°=78°.
故选:C.
8.【解答】解:过点B作BH⊥AE于点H,过点E作EF⊥AB交AB的延长线于点F,
∵菱形ABCD中,AB=2,
∴BC=2,
∵BE=2EC,
∴BE=,CE=,
∵∠D=120°,
∴∠ABE=120°,
∴∠EBF=60°,
∴BF=BE=,EF=,
∴AF=AB+BF=2+=,
∴AE===,
∵S△ABE=AB•EF,
∴BH===.
故选:A.
9.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵∠ACD=20°,
∴∠CAB=20°,
∵BE⊥AB,
∴∠AEB=90°﹣20°=70°,
∴∠CEB=180°﹣70°=110°,
故选:C.
10.【解答】解:∵∠A=∠CDE,
∴DE∥AB,
∵AD=DC,
∴CE=BE,
∴DE是△CAB的中位线,
∴AB=2DE=20m,
答:A,B间的距离是20m,
故选:C.
11.【解答】解:如图作B′H⊥AD于H交BC于M.
∵∠B′HD=∠HDF=∠DFB′=90°,
∴四边形DFB′H是矩形,
∵FD=FB′,
∴四边形DFB′H是正方形,设边长为x,则AH=6﹣x,HB′=x,
在Rt△AHB′中,∵AB′2=AH2+HB′2,
∴62=(6﹣x)2+x2,
解得x=3,
∴B′M=CF=6﹣3,
∵△AHB′∽△B′ME,
∴=,
∴=,
∴EB′=6﹣6,
∴BE=B′E=6﹣6,
故选:D.
12.【解答】解:∵在菱形ABCD中,AB=5,∠ABC=120°,
∴∠A=∠C=60°,AB=AD,
∴△ABD是等边三角形,
∴AB=AD=BD=5.
故选:D.
二.填空题(共8小题)
13.【解答】解:如图,设=,
则有++•••+=(+)+(+2)+•••+(+22)
=22+23×11,
∵+23=,
∴++•••+=11+11+23×11=11+11(+23)=11+11,
故答案为:11+11.
14.【解答】解:设B(m,n),则OA=BC=﹣m,AB=n,
∵BD=2AD,
∴AD=n,
∴D(m,n),
∵D在反比例函数y=图象上,
∴k=mn,
而E也在反比例函数y=图象上,yE=n,
∴E(m,n),
∴CE=﹣m,
∵将△BDC沿CD翻折得△FDC,
∴BC=FC=﹣m,
∵EF∥AB,
∴∠CEF=∠B=90°,
在Rt△CEF中,CE2+EF2=CF2,
∴(﹣m)2+(4)2=(﹣m)2,
解得m=6(舍去)或m=﹣6,
∴CE=2,BE=4,
过D作DH⊥EF于H,如图:
∵EF∥AB,DH⊥EF,∠B=90°,
∴四边形BDHE是矩形,
∴DH=BE=4,EH=BD=n,
在Rt△DHF中,DH2+HF2=DF2,
∴42+(4﹣n)2=(n)2,
解得n=,
∴k=mn=×(﹣6)×=﹣9.
故答案为:﹣9.
15.【解答】解:延长OE,与BG交于M点,如图所示:
∵O为BF中点,EF∥BG,
∴OB=OF,∠EFO=MBO,
在△OEF和△OMB中,
∴△OEF≌△OMB(ASA),
∴EF=BM,OE=OM,
设EC=3x(0<3x<6),
则CG=EF=BM=4x,
∴MC=BC﹣BM=8﹣4x,
∴EM====,
当EM最小时,OE最小,此时x=,
即EC=3x=,
EM==,
∴OE=EM=.
故答案为:.
16.【解答】解:第二个图形有1+3=4个正六边形;
第三个图形有1+3+3=7个正六边形;
…
第n个图形中,有1+3(n﹣1)=(3n﹣2)个正六边形.
第2020个图形中,共有2020×3﹣2=6058个正六边形.
故答案为:6058.
17.【解答】解:如图,连接EQ,FQ,过点Q作QH⊥AC于H,
∵DQ=2CQ,
∴设CQ=a,则DQ=2a,
∵四边形ABCD是正方形,
∴AD=CD=3a,∠ACD=45°,AC=3a,
∵将正方形ABCD折叠,使A点落在边CD上的点Q处,
∴AF=FQ,AE=EQ,
∵FQ2=DF2+DQ2,
∴AF2=(3a﹣AF)2+4a2,
∴AF=a,
∵HQ⊥AC,∠ACD=45°,
∴∠ACD=∠QCH=45°,
∴QH=HC=a,
∴AH=a,
∵EQ2=HQ2+EH2,
∴AE2=(a﹣AE)2+a2,
∴AE=,
∴=,
故答案为:.
18.【解答】解:
如图1中,当四边形DEFG为正方形时,设正方形边长为x,
则AB==5,CD=x,AD=x,
∵AD+CD=AC,
∴x+x=3,x=,
此时d=.
如图2,当四边形DEFG为菱形时,设菱形边长为m,
∵DE∥AB,
∴,
即,m=,
此时d=.
如图3,当四边形DEBG为菱形时,设边长为n,
则由DE∥AB可知,
即,n=,
此时d=.
由以上图形观察可得,
当d=或d<时,菱形的个数为1.
故答案为:d=或d<.
19.【解答】解:过A作AE⊥l1于E,过C点作CF⊥l2于F,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∴∠ABE=∠BCF=90°﹣∠CBF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=1,EB=CF=3,
∴AB2=AE2+EB2=12+32=10,
∴S正方形ABCD=10,
故答案为:10.
20.【解答】解:设①②③三个等腰直角三角形的边长分别为a,b,c,
∴①②③三个等腰直角三角形的周长分别为:(2+)a,(2+)b,(2+)c,
∴每两个等腰直角三角形的周长之差分别为:(2+)(a﹣c),(2+)(a﹣b),(2+)(b﹣c)
∵EF=BE﹣BF=a﹣b,
∴不能求①②两个等腰直角三角形之差,
∵∠BFC=90°,∠GFC=45°
∴∠EFG=45°
∴EF=DG=a﹣c
∴能求①③两个等腰直角三角形之差,
∵b=c,
∴b﹣c=c﹣c与EF无关,
故答案为:①③
三.解答题(共5小题)
21.【解答】证明:(1)如图①将△ABC绕顶点B按顺时针转60°得到△BDE,连接AC,BD.
由旋转可知△ABC≌△DBE,
∴AC=DE,BC=DE,
∵∠CBE=60°,
∴△BCE为等边三角形.
∴EC=BC,∠BCE=60°.
∵∠C=30°,
∴∠DCE=90°.
在Rt△DCE中,根据勾股定理得,
DC2+CE2=DE2.
∴DC2+BC2=AC2,
∴四边形ABCD是勾股四边形
(2)以DC为边作等边三角形DCE,作EF⊥BC于点F,连接BD,BE,
∵AB=AD,∠DAB=60°,
∴△ABD为等边三角形,
∴AD=BD,∠ADB=60°,
∵△DEC为等边三角形,
∴∠EDC=∠ECD=60°,DE=DC,
∴∠ADC=∠BDE,
∴△ADC≌△BDE(SAS),
∴AC=BE,
∵∠DCB=60°,
∴∠BCE=120°,
∴∠ECF=60°,
设CD=CE=a,BC=8﹣a,
在Rt△CEF中,cos∠ECF=,
∴CF=,EF=a,
∴BF=8﹣a,
∵∠EFB=90°,
∴BE2=EF2+BF2
=+
=+288,
∵1>0,
∴a=4时,BE2取最小值是288,
∴BE=12,
∵AC=AE,
∴AC的最小值12.
22.【解答】解:(1)如图1,∵AB=AC,
∴设AB=6x,AC=5x,
∴AC=BC=5x,
∵BE⊥AC,BE=3,
∴,
解得:x=,AE=x=,CE=x=,
∴BC=5×=,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AEF∽△CEB,
∴=,即=,
∴AF=.
(2)BG2+CG2=2EG2.理由如下:
如图2,过点G作GH∥AC交AB于点H,交BE于点K,作GM⊥AC于点M,
∵AC=BC,
∴∠CBA=∠CAB,
∵GH∥AC,
∴∠GHB=∠CAB,
∴∠CBA=∠GHB,
∴GH=GB,
∵GQ⊥AB,
∴BQ=HQ,即BH=2BQ,
∵PG=2BQ,
∴BH=PG,
∵BE⊥AC,
∴∠BEC=90°,
∵GH∥AC,
∴∠BKG=∠BEC=90°,
∴∠GKE=180°﹣∠BKG=90°,∠BKH=∠BEC=90°,
∴∠BKH=∠GKP,
∵∠HBK+∠BHK=90°,∠PGK+∠BHK=90°,
∴∠HBK=∠PGK,
∴△BHK≌△GPK(AAS),
∴BK=GK,
∴∠KBG=∠KGB=45°,
∴KG=BG•sin∠KBG=BG•sin45°=BG,
∵GH∥AC,
∴∠BCE=∠BGK=45°,
∵∠CMG=90°,
∴GM=CG•sin∠GCM=CG•sin45°=CG,
∵∠GME=∠MEK=∠EKG=90°,
∴四边形EKGM是矩形,
∴EK=GM=CG,
在Rt△EGK中,∵EK2+KG2=EG2,
∴(BG)2+(CG)2=EG2,
∴BG2+CG2=EG2,
∴BG2+CG2=2EG2.
23.【解答】(1)解:∵四边形ABCD是平行四边形,
∴AB=CD=,OB=OD,
∵AD⊥BD,
∴BD===3,
∴OD=BD=,
∴△AOD的面积=AD×OD=×2×=;
(2)证明:连接GF,如图所示:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵点E,F,G分别是线段AB,OD,OC的中点,
∴BE=AB,GF是△OCD的中位线,
∴GF∥CD,GF=CD,
∴GF∥BE,GF=BE,
∴四边形BEFG是平行四边形,
∴EF∥BG.
24.【解答】解:(1)∵DE⊥AB,
∴AE===2,
∵四边形ABCD是平行四边形,
∴AB=CD=10,
∴BE=AB﹣AE=8;
(2)方法一:如图,过点E作EM⊥HE,交HF的延长线于点M,连接AP,GE,DF,
∵AE=PE,且DE⊥AE,
∴∠PAE=∠APE=45°,
∵∠AGP=∠AEP=90°,
∴点A,点E,点P,点G四点共圆,
∴∠PGE=∠PAE=45°,
∵∠DGF=∠DEF=90°,
∴点D,GH,点E,点F四点共圆,
∴∠EDF=∠PGE=45°,
∴∠EDF=∠DFE=45°,
∴DE=EF,
∵∠DHF=∠DEF=90°,
∴点D,点E,点F,点H四点共圆,
∴∠DFE=∠DHE=45°,∠EDF=∠EHF=45°,且EM⊥EH,
∴∠M=∠EHF=45°,
∴EH=EM,
∴HM=EH,
∵∠DEB=∠HEM=90°,
∴∠DEH=∠FEM,且∠DHE=∠M=45°,DE=EF,
∴△DEH≌△FEM(AAS)
∴DH=MF,
∴DH+HF=MF+HF=HM=EH.
方法二:∵∠AED=∠DGP=∠PEF=90°,∠DPG=∠EPF,
∴∠ADE=∠PFE,
∴△ADE≌△PFE(AAS),
∴DE=EF,
延长BD到Q使DQ=FH,
∵FH⊥BD,
∴∠EDB+∠DBE=∠HFB+∠HBF=90°,
∴∠EPB=∠HFB,
∴∠QDE=∠HFE,
∴△EQD≌△EFH(SAS),
∴∠QED=∠HEF,QE=EH,
∴∠QEH=∠DEB=90°,
∴△QEH是等腰直角三角形,
∴QH=EH,
∴DH+FH=EH.
25.【解答】解:(1)如图1中,∵四边形ABCD是菱形,
∴AB=BC=CD=AD=10,AB∥CD
∵PD=4,
∴PC=6,
∵PB⊥CD,
∴PB⊥AB,
∴∠CPB=∠ABP=90°,
在RT△PCB中,∵∠CPB=90°PC=6,BC=10,
∴PB===8,
在RT△ABP中,∵∠ABP=90°,AB=10,PB=8,
∴PA===2.
(2)△OMN是等腰三角形.
理由:如图2中,延长PM交BC于E.
∵四边形ABCD是菱形,
∴AC⊥BD,CB=CD,
∵PE⊥AC,
∴PE∥BD,
∴=,
∴CP=CE,
∴PD=BE,
∵CP=CE,CM⊥PE,
∴PM=ME,
∵PN=NB,
∴MN=BE,
∵BO=OD,BN=NP,
∴ON=PD,
∴ON=MN,
∴△OMN是等腰三角形.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
相关试卷
这是一份专题25 统计初步-全国初三数学自主招生专题大揭秘(含答案详解),共36页。试卷主要包含了的数据,绘制了如图所示的折线图,如下等内容,欢迎下载使用。
这是一份专题24 概率-全国初三数学自主招生专题大揭秘(含答案详解),共23页。
这是一份专题20 平面向量-全国初三数学自主招生专题大揭秘(含答案详解),共20页。试卷主要包含了定义等内容,欢迎下载使用。









