中考数学三轮冲刺《圆》解答题冲刺练习02（含答案）

中考数学三轮冲刺《圆》解答题冲刺练习02

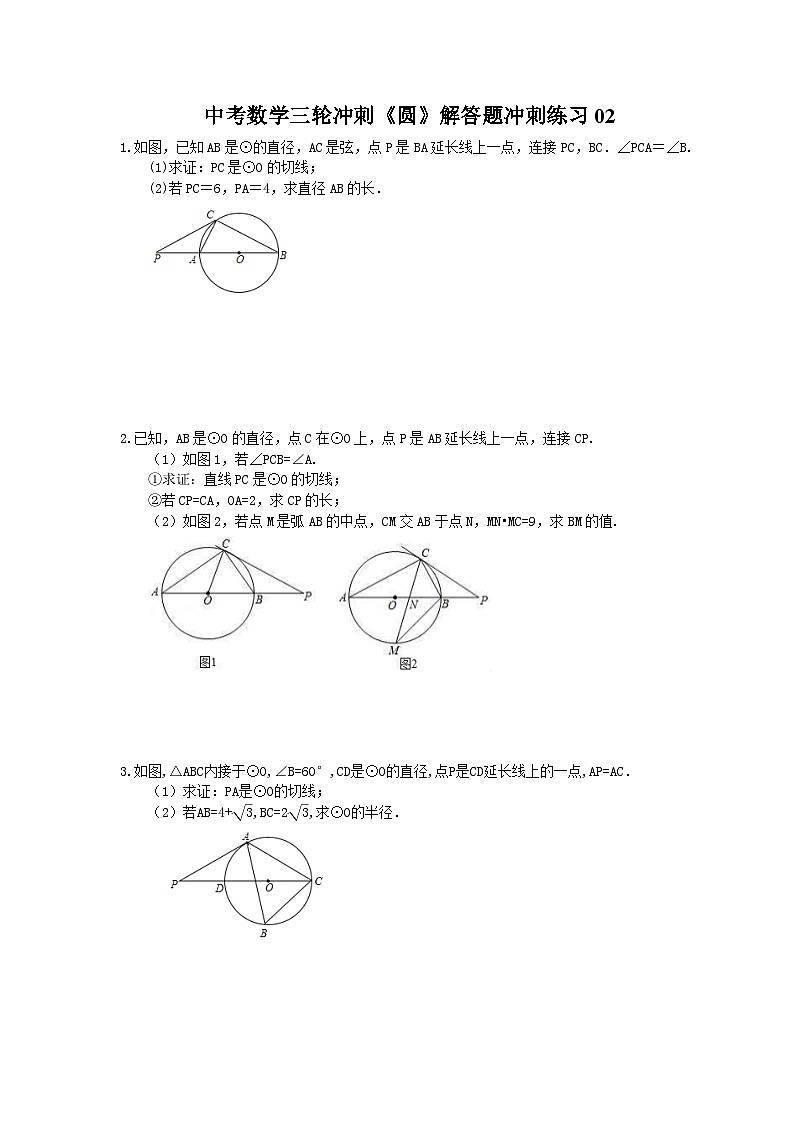
1.如图，已知AB是⊙的直径，AC是弦，点P是BA延长线上一点，连接PC，BC．∠PCA＝∠B.

(1)求证：PC是⊙O的切线；

(2)若PC＝6，PA＝4，求直径AB的长．

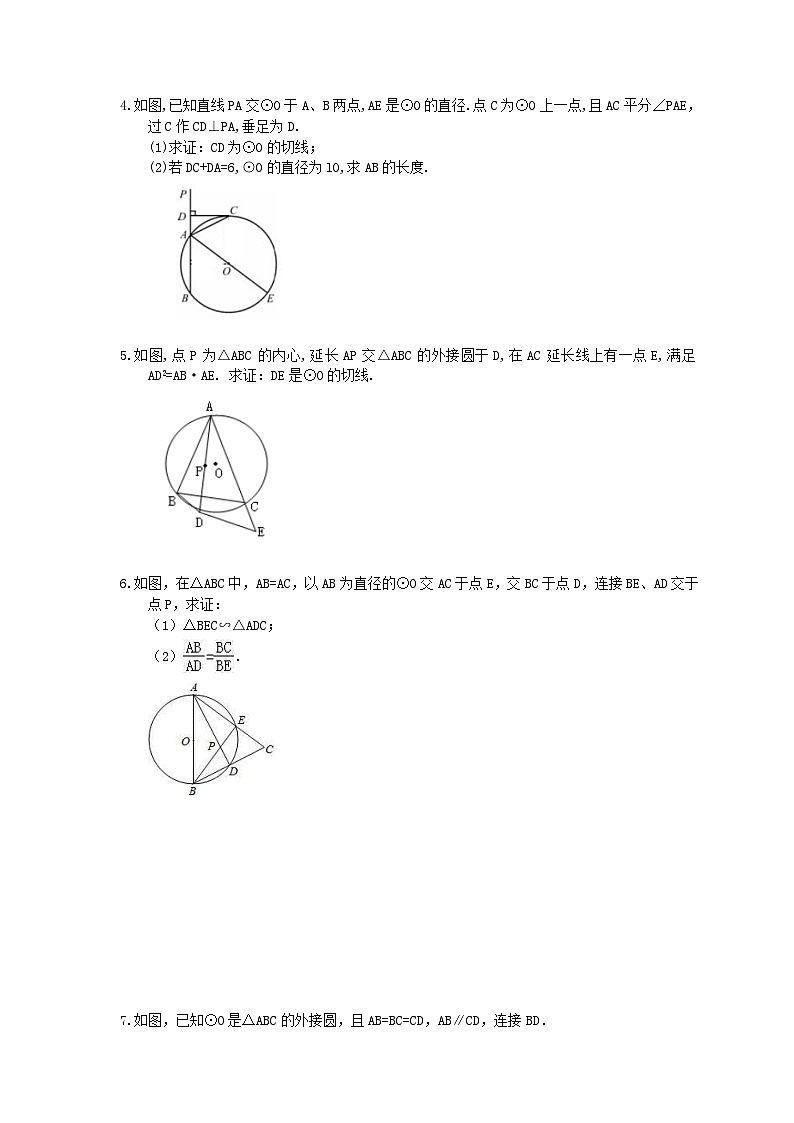
2.已知，AB是⊙O的直径，点C在⊙O上，点P是AB延长线上一点，连接CP.

（1）如图1，若∠PCB=∠A.

①求证：直线PC是⊙O的切线；

②若CP=CA，OA=2，求CP的长；

（2）如图2，若点M是弧AB的中点，CM交AB于点N，MN•MC=9，求BM的值.

3.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,AP=AC．

（1）求证：PA是⊙O的切线；

（2）若AB=4+,BC=2,求⊙O的半径．

4.如图,已知直线PA交⊙0于A、B两点,AE是⊙0的直径.点C为⊙0上一点,且AC平分∠PAE，过C作CD⊥PA,垂足为D.

(1)求证：CD为⊙0的切线；

(2)若DC+DA=6,⊙0的直径为l0,求AB的长度.

5.如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB·AE. 求证：DE是⊙O的切线.

6.如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC于点E，交BC于点D，连接BE、AD交于点P，求证：

（1）△BEC∽△ADC；

（2）．

7.如图，已知⊙O是△ABC的外接圆，且AB=BC=CD，AB∥CD，连接BD．

（1）求证：BD是⊙O的切线；

（2）若AB=10，cos∠BAC=0.6，求BD的长及⊙O的半径．

8.如图，以AB为直径的⊙O外接于△ABC，过A点的切线AP与BC的延长线交于点P，∠APB的平分线分别交AB，AC于点D，E，其中AE，BD(AE＜BD)的长是一元二次方程x2－5x＋6=0的两个实数根.

(1)求证：PA·BD=PB·AE；

(2)在线段BC上是否存在一点M，使得四边形ADME是菱形？若存在，请给予证明，并求其面积；若不存在，说明理由.

0.中考数学三轮冲刺《圆》解答题冲刺练习02（含答案）参考答案

一         、解答题

1.证明：(1)连接OC，如图所示：

∵AB是⊙的直径，

∴∠ACB＝90°，即∠1＋∠2＝90°，

∵OB＝OC，

∴∠2＝∠B，

又∵∠PCA＝∠B，

∴∠PCA＝∠2，

∴∠1＋∠PCA＝90°，即PC⊥OC，

∴PC是⊙O的切线；

(2)∵PC是⊙O的切线，

∴PC2＝PA•PB，

∴62＝4×PB，解得：PB＝9，

∴AB＝PB﹣PA＝9﹣4＝5．

2.（1）①证明：如图1中，

∵OA=OC，

∴∠A=∠ACO，

∵∠PCB=∠A，

∴∠ACO=∠PCB，

∵AB是⊙O的直径，

∴∠ACO+∠OCB=90°，

∴∠PCB+∠OCB=90°，即OC⊥CP，

∵OC是⊙O的半径，

∴PC是⊙②∵CP=CA，

∴∠P=∠A，

∴∠COB=2∠A=2∠P，

∵∠OCP=90°，

∴∠P=30°，

∵OC=OA=2，

∴OP=2OC=4，

∴.

（2）解：如图2中，连接MA.

∵点M是弧AB的中点，

∴=，

∴∠ACM=∠BAM，

∵∠AMC=∠AMN，

∴△AMC∽△NMA，

∴AM2=MC•MN，

∵MC•MN=9，

∴AM=3，

∴BM=AM=3.

3.解：（1）证明：连接OA．

∵∠B=60°，∴∠AOC=2∠B=120°．
又∵OA=OC，∴∠OAC=∠OCA=30°．
又∵AP=AC，∴∠P=∠ACP=30°．

∴∠OAP=∠AOC-∠P=90°．∴OA⊥PA．
又∵点A在⊙O上，

∴PA是⊙O的切线．
（2）解：过点C作CE⊥AB于点E．
在Rt△BCE中，∠B=60°，BC=2，

∴BE=0.5BC=，CE=3．
∵AB=4+，∴AE=AB-BE=4．
∴在Rt△ACE中，AC=5．

∴AP=AC=5．
∴在Rt△PAO中，OA=．

∴⊙O的半径为．

4. (1)证明：连接OC,

∵点C在⊙0上，0A=OC,∴∠OCA=∠OAC，∵CD⊥PA，∴∠CDA=90°，

有∠CAD+∠DCA=90°，∵AC平分∠PAE，∴∠DAC=∠CAO。

∴∠DC0=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC=90°。

又∵点C在⊙O上，OC为⊙0的半径，∴CD为⊙0的切线．

(2)解：过0作0F⊥AB，垂足为F，∴∠OCA=∠CDA=∠OFD=90°，

∴四边形OCDF为矩形，∴0C=FD，OF=CD.

∵DC+DA=6，设AD=x，则OF=CD=6-x，∵⊙O的直径为10，∴DF=OC=5，∴AF=5-x，

在Rt△AOF中，由勾股定理得.即，化简得：

解得x=2或x=9。由AD<DF，知0<x<5，故x=2。

从而AD=2, AF=5-2=3.∵OF⊥AB，由垂径定理知，F为AB的中点，∴AB=2AF=6.

5.证明:连结DO，∵AD2=AB·AE，∠BAD＝∠DAE，∴△BAD∽△DAE，

∴∠ADB＝∠E. 又∵∠ADB＝∠ACB，∴∠ACB＝∠E，BC∥DE，

又∵OD⊥BC，∴OD⊥DE，故DE是⊙O的切线

6.证明：

（1）∵AB是⊙O的直径，

∴∠AEB=∠ADB=90°，∴∠CEB=∠CDA=90°，

∵∠C=∠C，∴△BEC∽△ADC；

（2）由（1）得：△BEC∽△ADC，∴，

∵AB=AC，∴．

7.解：

8.解：(1)证明：∵DP平分∠APB，∴∠APE=∠BPD.

∵AP与⊙O相切，∴∠BAP=∠BAC＋∠EAP=90°.

∵AB是⊙O的直径，∴∠ACB=∠BAC＋∠B=90°，

∴∠EAP=∠B，∴△PAE∽△PBD，

∴=，∴PA·BD=PB·AE.

(2)过点D作DF⊥PB于点F，作DG⊥AC于点G，

∵DP平分∠APB，AD⊥AP，DF⊥PB，∴AD=DF.

∵∠EAP=∠B，∴∠APC=∠BAC，易证DF∥AC，∴∠BDF=∠BAC，

由于AE，BD(AE＜BD)的长是x2－5x＋6=0，解得AE=2，BD=3，

∴由(1)可知：=，

∴cos∠APC==，∴cos∠BDF=cos∠APC=，∴=，

∴DF=2，∴DF=AE，

∴四边形ADFE是平行四边形.

∵AD=DF，∴四边形ADFE是菱形，此时点F即为点M.

∵cos∠BAC=cos∠APC=，

∴sin∠BAC=，∴=，∴DG=，

∴在线段BC上存在一点M，使得四边形ADME是菱形，

其面积为DG·AE=2×=.