中考数学三轮冲刺《圆》解答题冲刺练习10（含答案）

中考数学三轮冲刺《圆》解答题冲刺练习10

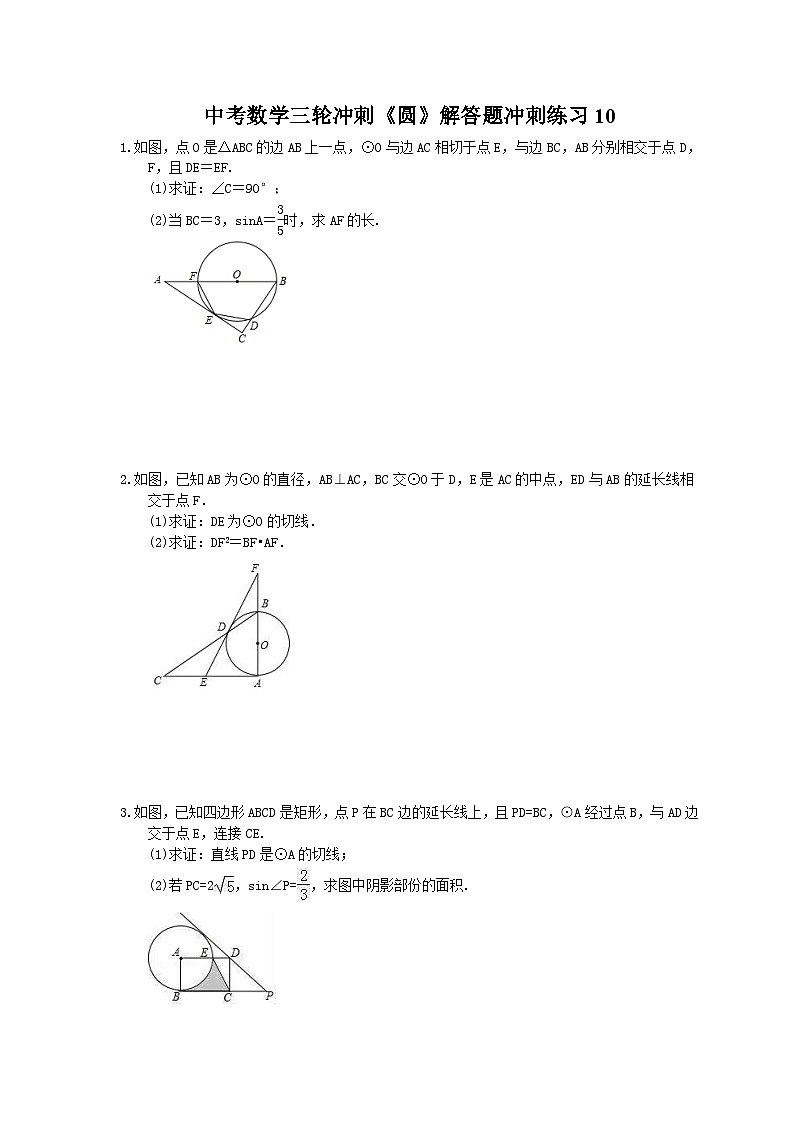
1.如图，点O是△ABC的边AB上一点，⊙O与边AC相切于点E，与边BC，AB分别相交于点D，F，且DE＝EF.

(1)求证：∠C＝90°；

(2)当BC＝3，sinA＝时，求AF的长.

2.如图，已知AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，ED与AB的延长线相交于点F．

(1)求证：DE为⊙O的切线．

(2)求证：DF2＝BF•AF．

3.如图，已知四边形ABCD是矩形，点P在BC边的延长线上，且PD=BC，⊙A经过点B，与AD边交于点E，连接CE.

(1)求证：直线PD是⊙A的切线；

(2)若PC=2，sin∠P=，求图中阴影部份的面积.

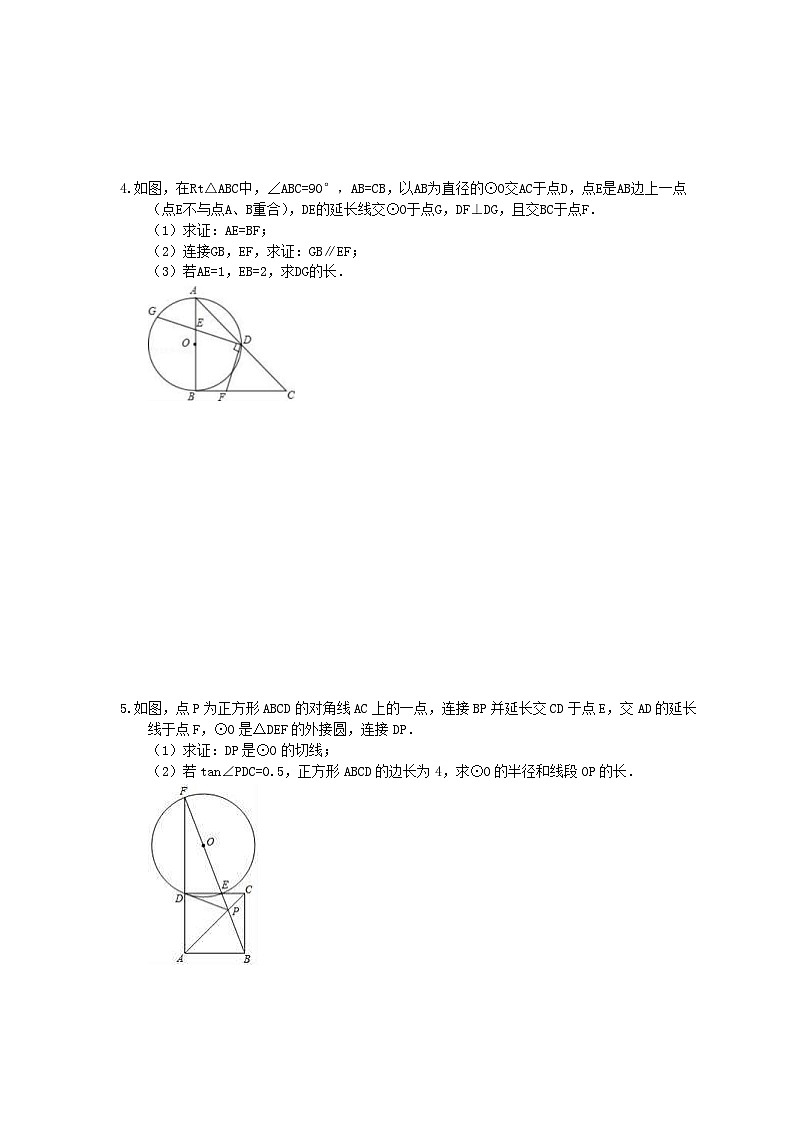
4.如图，在Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．

（1）求证：AE=BF；

（2）连接GB，EF，求证：GB∥EF；

（3）若AE=1，EB=2，求DG的长．

5.如图，点P为正方形ABCD的对角线AC上的一点，连接BP并延长交CD于点E，交AD的延长线于点F，⊙O是△DEF的外接圆，连接DP．

（1）求证：DP是⊙O的切线；

（2）若tan∠PDC=0.5，正方形ABCD的边长为4，求⊙O的半径和线段OP的长．

6.如图，DC是⊙O的直径，点B在圆上，直线AB交CD延长线于点A，且∠ABD=∠C．

（1）求证：AB是⊙O的切线；

（2）若AB=4cm，AD=2cm，求tanA的值和DB的长．

7.如图，AB为⊙O直径，C是⊙O上一点，CO⊥AB于点O，弦CD与AB交于点F．过点D作⊙O的切线交AB的延长线于点E，过点A作⊙O的切线交ED的延长线于点G．

（1）求证：△EFD为等腰三角形；

（2）若OF：OB=1：3，⊙O的半径为3，求AG的长．

8.如图,已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于B．

（1）求证：AD是⊙O的切线；

（2）若⊙O的半径为3,AB=4,求AD的长．

0.中考数学三轮冲刺《圆》解答题冲刺练习10（含答案）参考答案

一         、解答题

1.解：(1)连接OE，BE，

∵DE＝EF，

∴

∴∠OBE＝∠DBE

∵OE＝OB，

∴∠OEB＝∠OBE

∴∠OEB＝∠DBE，

∴OE∥BC

∵⊙O与边AC相切于点E，

∴OE⊥AC

∴BC⊥AC

∴∠C＝90°

(2)在△ABC，∠C＝90°，BC＝3，sinA＝

∴AB＝5，

设⊙O的半径为r，则AO＝5﹣r，

在Rt△AOE中，sinA＝＝＝,

∴r＝

∴AF＝5﹣2×＝.

2.证明：(1)连AD，OD，如图所示：

∵AB为⊙O的直径，

∴∠ADB＝∠ADC＝90°，

∵E是AC的中点，

∴EA＝ED，

∴∠EDA＝∠EAD，

∵OD＝OA，

∴∠ODA＝∠OAD，

∴∠EDO＝∠EAO，

∵AB⊥AC，

∴∠EAO＝90°，

∴∠EDO＝90°，

∴DE为⊙O的切线；

(2)证明：∵DE为⊙O的切线，

∴∠ODF＝∠FDB＋∠ODB＝∠FAD＋∠OBD＝90°，

∵OD＝OB，

∴∠ODB＝∠OBD，

∴∠FDB＝∠FAD，

又∵∠F为公共角，

∴△FDB∽△FAD，

∴＝，

∴DF2＝BF•AF．

3.解：(1)证明：如图，过A作AH⊥PD，垂足为H.

∵四边形ABCD是矩形，

∴AD=BC，AD∥BC，∠PCD=∠BCD=90°，

∴∠ADH=∠P，∠AHD=∠PCD=90°，

又∵PD=BC，

∴AD=PD，

∴△ADH≌△DPC，

∴AH=CD.

∵CD=AB，且AB是⊙A的半径，

∴AH=AB，即AH是⊙A的半径，

∴PD是⊙A的切线.

(2)如图，在Rt△PDC中，sin∠P==，PC=2，

令CD=2x，PD=3x，由勾股定理得：

(3x)2﹣(2x)2=(2)2.解得：x=2，

∴CD=4，PD=6，

∴AB=AE=CD=4，AD=BC=PD=6，DE=2，

∵矩形ABCD的面积为6×4=24，Rt△CED的面积为×4×2=4，

扇形ABE的面积为π×42=4π.

∴图中阴影部份的面积为24﹣4﹣4π=20﹣4π.

4.解：

（1）证明：连接BD，在Rt△ABC中，∠ABC=90°，AB=BC，

∴∠A=∠C=45°，

∵AB为圆O的直径，∴∠ADB=90°，即BD⊥AC，

∴AD=DC=BD=AC，∠CBD=∠C=45°，∴∠A=∠FBD，

∵DF⊥DG，∴∠FDG=90°，∴∠FDB+∠BDG=90°，

∵∠EDA+∠BDG=90°，∴∠EDA=∠FDB，

在△AED和△BFD中，，∴△AED≌△BFD（ASA），

∴AE=BF；

（2）证明：连接EF，BG，∵△AED≌△BFD，∴DE=DF，

∵∠EDF=90°，∴△EDF是等腰直角三角形，∴∠DEF=45°，

∵∠G=∠A=45°，∴∠G=∠DEF，∴GB∥EF；

（3）∵AE=BF，AE=1，∴BF=1，

在Rt△EBF中，∠EBF=90°，∴根据勾股定理得：EF2=EB2+BF2，

∵EB=2，BF=1，∴EF==，

∵△DEF为等腰直角三角形，∠EDF=90°，∴cos∠DEF=，

∵EF=，∴DE=×=，

∵∠G=∠A，∠GEB=∠AED，∴△GEB∽△AED，

∴=，即GE•ED=AE•EB，∴•GE=2，即GE=，则GD=GE+ED=．

5.解：

（1）连接OD，

∵正方形ABCD中，CD=BC，CP=CP，∠DCP=∠BCP=45°，

∴△CDP≌△CBP（SAS），

∴∠CDP=∠CBP，

∵∠BCD=90°，

∴∠CBP+∠BEC=90°，

∵OD=OE，

∴∠ODE=∠OED，

∠OED=∠BEC，

∴∠BEC=∠OED=∠ODE，

∴∠CDP+∠ODE=90°，

∴∠ODP=90°，

∴DP是⊙O的切线；

（2）∵∠CDP=∠CBE，

∴tan，∴CE=，∴DE=2，

∵∠EDF=90°，∴EF是⊙O的直径，

∴∠F+∠DEF=90°，∴∠F=∠CDP，

在Rt△DEF中，，∴DF=4，

∴==2，∴，

∵∠F=∠PDE，∠DPE=∠FPD，∴△DPE∽△FPD，

∴，设PE=x，则PD=2x，

∴，解得x=，

∴OP=OE+EP=．

6.解：

（1）证明：连结OB，如图所示：

∵OB=OD，∴∠ODB=∠OBD，

∵DC是⊙O的直径，∴∠DBC=90°，∴∠CDB+∠C=90°，

∵∠ABD=∠C，∴∠OBD+∠ABD=90°，即∠OBA=90°，

∴OB⊥AB，∴AB是⊙O的切线；

（2）解：设半径为r，则OA=x+2，

在Rt△AOB中，根据勾股定理得：x2+42=（x+2）2，解得：r=3，

∴tanA==，

∵∠A=∠A，∠ABD=∠C，∴△ADB∽△ACB，∴==，

设DB=x，则BC=2x，

∵CD=6，∴由勾股定理得：x2+（2x）2=62，解得：x=，

即DB的长为．

7.（1）证明：连接OD，

∵OC=OD，

∴∠C=∠ODC，

∵OC⊥AB，

∴∠COF=90°，

∴∠OCD+∠CFO=90°，

∵GE为⊙O的切线，

∴∠ODC+∠EDF=90°，

∵∠EFD=∠CFO，

∴∠EFD=∠EDF，

∴EF=ED．

（2）解：∵OF：OB=1：3，⊙O的半径为3，

∴OF=1，

∵∠EFD=∠EDF，

∴EF=ED，

在Rt△ODE中，OD=3，DE=x，则EF=x，OE=1+x，

∵OD2+DE2=OE2，

∴32+x2=（x+1）2，解得x=4，

∴DE=4，OE=5，

∵AG为⊙O的切线，

∴AG⊥AE，

∴∠GAE=90°，

而∠OED=∠GEA，

∴Rt△EOD∽Rt△EGA，

∴=，即=，

∴AG=6．

8.解：

（1）证明：如图，连接AO并延长交⊙O于点E，连接BE，则∠ABE=90°，

∴∠EAB+∠E=90°．

∵∠E=∠C，∠C=∠BAD，

∴∠EAB+∠BAD=90°．

∴AD是⊙O的切线．

（2）解：由（1）可知∠ABE=90°，直径AE=2AO=6，AB=4，

∴．

∵∠E=∠C=∠BAD，BD⊥AB，

∴cos∠BAD=cos∠E．

∴．

∴．