中考数学三轮冲刺《圆》解答题冲刺练习15（含答案）

中考数学三轮冲刺《圆》解答题冲刺练习15

1.如图，⊙O的直径AD长为6，AB是弦，CD∥AB，且CD=.

(1)求∠C的度数；

(2)求证：BC是⊙O的切线.

2.如图，在Rt△ABC中，∠C＝90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．

(1)求证：AC是⊙O的切线；

(2)若OB＝10，CD＝8，求BE的长．

3.如图，△ABC中，AB=AC，点D为BC边上一点，且DA=DC，过A，B，D三点作⊙O，AE是⊙O的直径，连接DE．

（1）求证：AC是⊙O的切线；

（2）若sinC=0.8，AC=12，求⊙O的直径．

4.如图，在Rt△ABC中，∠C=90°，BD为∠ABC的平分线，DF⊥BD交AB于点F，△BDF的外接圆⊙O与边BC相交于点M，过点M作AB的垂线交BD于点E，交⊙O于点N，交AB于点H，连结FN.

(1)求证：AC是⊙O的切线；

(2)若AF=4，tan∠N=，求⊙O的半径长；

(3)在(2)的条件下，求MN的长.

5.如图，在△ABC中，AB＝AC，AE是∠BAC的平分线，∠ABC的平分线BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交AB于点F.

(1)求证：AE为⊙O的切线；

(2)当BC＝4，AC＝6时，求⊙O的半径；

(3)在(2)的条件下，求线段BG的长.

6.定义：若△ABC中，其中一个内角是另一个内角的一半，则称△ABC为“半角三角形”.

（1）若Rt△ABC为半角三角形，∠A=90°，则其余两个角的度数为　   　.

（2）如图1，在▱ABCD中，∠C=72°，点E在边CD上，以BE为折痕，将△BCE向上翻折，点E恰好落在AD边上的点F，若BF⊥AD，求证：△EDF为半角三角形；

（3）如图2，以△ABC的边AB为直径画圆，与边AC交于M，与边BC交于N，已知△ABC的面积是△CMN面积的4倍.

①求证：∠C=60°.

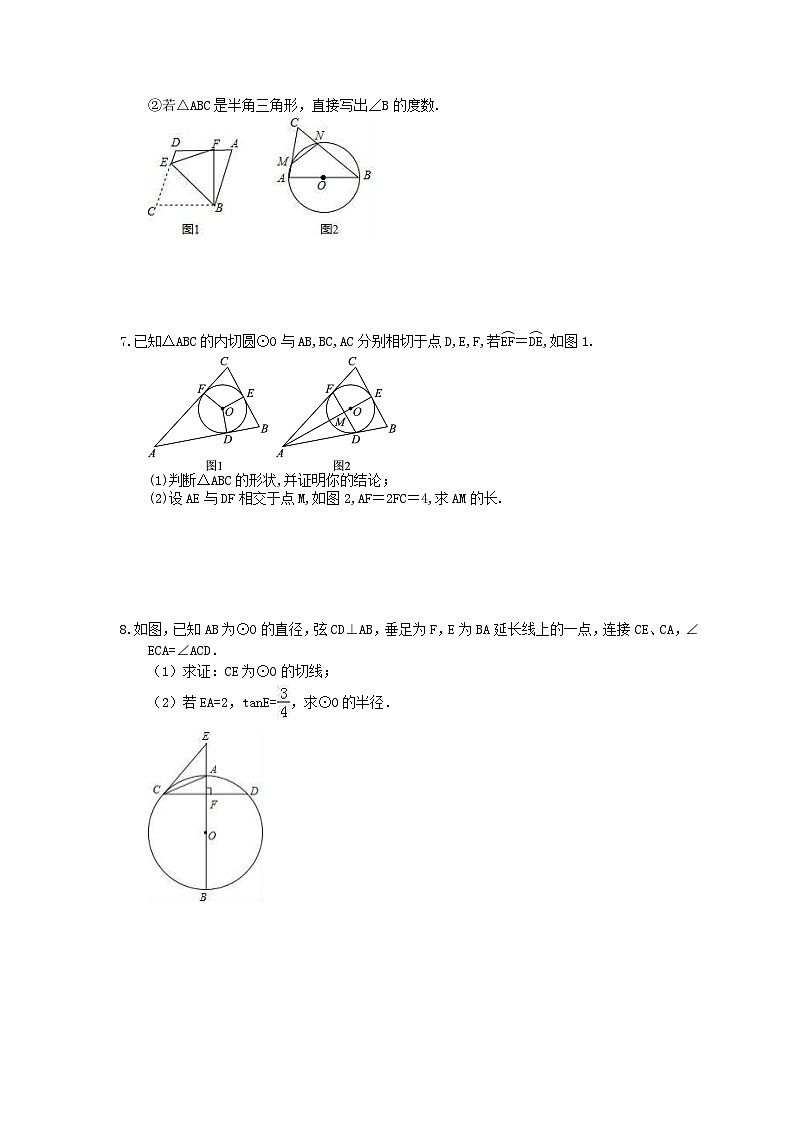
②若△ABC是半角三角形，直接写出∠B的度数.

7.已知△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,若＝,如图1.

(1)判断△ABC的形状,并证明你的结论；

(2)设AE与DF相交于点M,如图2,AF＝2FC＝4,求AM的长.

8.如图，已知AB为⊙O的直径，弦CD⊥AB，垂足为F，E为BA延长线上的一点，连接CE、CA，∠ECA=∠ACD．

（1）求证：CE为⊙O的切线；

（2）若EA=2，tanE=，求⊙O的半径．

0.中考数学三轮冲刺《圆》解答题冲刺练习15（含答案）参考答案

一         、解答题

1. (1)解：如图，连接BD，

∵AD为圆O的直径，

∴∠ABD=90°，

∴BD=AD=3，

∵CD∥AB，∠ABD=90°，

∴∠CDB=∠ABD=90°，

在Rt△CDB中，tanC=，

∴∠C=60°；

(2)连接OB，

∵BD=3，AD=6，

∴∠A=30°，

∵OA=OB，

∴∠OBA=∠A=30°，

∵CD∥AB，∠C=60°，

∴∠ABC=180°﹣∠C=120°，

∴∠OBC=∠ABC﹣∠ABO=120°﹣30°=90°，

∴OB⊥BC，

∴BC为圆O的切线.

2.证明：(1)连接OD，∵BD为∠ABC平分线，

∴∠1＝∠2，

∵OB＝OD，

∴∠1＝∠3，

∴∠2＝∠3，

∴OD∥BC，

∵∠C＝90°，

∴∠ODA＝90°，

则AC为圆O的切线；

(2)过O作OG⊥BC，

∴四边形ODCG为矩形，

∴GC＝OD＝OB＝10，OG＝CD＝8，

在Rt△OBG中，利用勾股定理得：BG＝6，

∴BC＝BG＋GC＝6＋10＝16，

∵OD∥BC，∴△AOD∽△ABC，

∴＝，即＝，解得：OA＝，

∴AB＝＋10＝，

连接EF，∵BF为圆的直径，

∴∠BEF＝90°，

∴∠BEF＝∠C＝90°，

∴EF∥AC，∴＝，即＝，

解得BE＝12．

3.解：

（1）证明：∵AB=AC，AD=DC，∴∠C=∠B，∠1=∠C，∴∠1=∠B，

又∵∠E=∠B，∴∠1=∠E，

∵AE是⊙O的直径，∴∠ADE=90°，∴∠E+∠EAD=90°，

∴∠1+∠EAD=90°，即∠EAC=90°，∴AE⊥AC，

∴AC是⊙O的切线；

（2）解：过点D作DF⊥AC于点F，如图，

∵DA=DC，∴CF=AC=3，在Rt△CDF中，∵sinC==，

设DF=4x，DC=5x，∴CF==3x，

∴3x=3，解得x=1，∴DC=5，∴AD=5，

∵∠ADE=∠DFC=90°，∠E=∠C，∴△ADE∽△DFC，

∴=，即=，解得AE=，

即⊙O的直径为．

4. (1)证明：如图，连结OD，

∵OD=OB，∴∠ODB=∠OBD，

∵BD为∠ABC的平分线，

∴∠DBC=∠OBD，

∴∠ODB=∠DBC，

∴OD∥BC，

∵AC⊥BC，

∴AC⊥OD，

∴AC是⊙O的切线；

(2)解：∵OD∥BC，

∴∠AOD=∠ABC，

∵∠N=∠ABC，

∴∠AOD=∠N，

在Rt△AOD中，

∵tan∠AOD=tan∠N==，

∴，即5OD=3AO，

设⊙O的半径为r，则5r=3(r+4)，解得：r=6，

∴⊙O的半径长为6；

(3)解：如图，连结BN，

∵BF为⊙O的直径，

∴BN⊥FN，

∴∠NBH+∠BFN=90°，

∵MN⊥FB，

∴∠HNF+∠BFN=90°，

∴∠FNH=∠NBH，

∴tan∠NBH=tan∠FNH=，

∴cos∠NBH=，sin∠NBH=，

∴在Rt△FBN中，BN=BF•cos∠NBF=12×=，

∴在Rt△HBN中，HN=BN•sin∠NBH=×=，

由垂径定理可得：MN=2HN=.

5. (1)证明：连接OM，如图1，

∵BM是∠ABC的平分线，

∴∠OBM＝∠CBM，

∵OB＝OM，

∴∠OBM＝∠OMB，

∴∠CBM＝∠OMB，

∴OM∥BC，

∵AB＝AC，AE是∠BAC的平分线，

∴AE⊥BC，

∴OM⊥AE，

∴AE为⊙O的切线；

(2)解：设⊙O的半径为r，

∵AB＝AC＝6，AE是∠BAC的平分线，

∴BE＝CE＝BC＝2，

∵OM∥BE，

∴△AOM∽△ABE，

∴＝，即＝，解得r＝，

即设⊙O的半径为；

(3)解：作OH⊥BE于H，如图，

∵OM⊥EM，ME⊥BE，

∴四边形OHEM为矩形，

∴HE＝OM＝，

∴BH＝BE﹣HE＝2﹣＝，

∵OH⊥BG，

∴BH＝HG＝，

∴BG＝2BH＝1.

6.解：（1）∵Rt△ABC为半角三角形，∠A=90°，

∴∠B=∠C=45°，或∠B=60°，∠C=30°或∠B=30°，∠C=60°，

∴其余两个角的度数为45°，45°或30°，60°，

故答案为45°，45°或30°，60°.

（2）如图1中，

∵平行四边形ABCD中，∠C=72°，

∴∠D=108°，

由翻折可知：∠EFB=72°，

∵EF⊥AD，

∴∠EFD=18°，

∴∠DEF=54°，

∴∠DEF=∠D，即△DEF是半角三角形.

（2）①如图2中，连接AN.

∵AB是直径，

∴∠ANB=90°，

∵∠C=∠C，∠CMN=∠B，

∴△CMN∽△CBA，

∴（）2=，即=，

在Rt△ACN中，sin∠CAN==，

∴∠CAN=30°，

∴∠C=60°.

②∵△ABC是半角三角形，∠C=60°，

∴∠B=30°或40°或80°或90°.

7.解：(1)△ABC为等腰三角形.

证明：∵△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,

∴∠CFO＝∠CEO＝∠BDO＝∠BEO＝90°.

∵四边形的内角和等于360°,

∴∠EOF＋∠C＝180°,∠DOE＋∠B＝180°.

∵＝,

∴∠EOF＝∠DOE,

∴∠B＝∠C,

∴AB＝AC,

∴△ABC为等腰三角形；

(2)∵AB,BC,AC分别切⊙O于D,E,F,AF＝2FC＝4,

又∵AB＝AC,

∴AB＝AC＝6,AD＝AF＝4,BD＝BE＝CE＝CF＝2,

∴AE⊥BC.

在Rt△ACE中,AE＝＝4.

∵＝＝,∠DAF＝∠BAC,

∴△DAF∽△ABC,∠ADF＝∠B,

∴FD∥BC,

∴＝,

∴AM＝＝＝.

8.

（1）证明：连接BC，OC，

∵AB为⊙O的直径，弦CD⊥AB，∴=，∴∠ACD=∠ABC，

∵OB=OC，∴∠ABC=∠OCB，∴∠ACD=∠OCB，

∵∠ECA=∠ACD．∴∠EAC=∠OCB，

∵∠OCB+∠OCA=90°，∴∠ECA+∠OCA=90°，∴∠OCE=90°，

∵点C在⊙O上，∴CE是⊙O的切线．

（2）在Rt△ECO中，tan∠E=，设OC=R，∴CE=R，OE=R+2，

∴（R）2+R2=（R+2）2，∴R=3或R=﹣（舍）．