新教材2023年高中数学第3章空间向量与立体几何1空间直角坐标系课件北师大版选择性必修第一册

这是一份新教材2023年高中数学第3章空间向量与立体几何1空间直角坐标系课件北师大版选择性必修第一册，共35页。

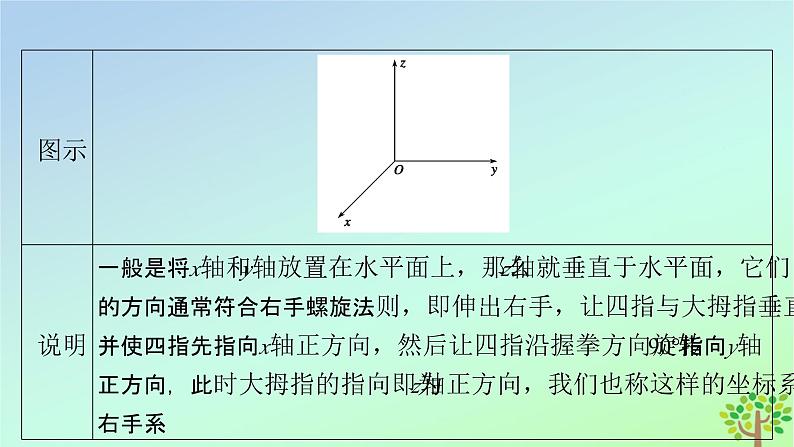
第三章　空间向量与立体几何§1　空间直角坐标系必备知识 · 探新知知识点 1空间直角坐标系坐标轴　坐标平面　135°　90°　空间一点P的坐标可用有序实数组(x，y，z)来表示，有序实数组(x，y，z)叫做点P在此空间直角坐标系中的坐标，记作P(x，y，z)，其中x叫做点P的_________，y叫做点P的_________，z叫做点P的_________.知识点 2空间中一点的坐标横坐标　纵坐标　竖坐标　(1)点P(x，y，z)到坐标原点O(0，0，0)的距离|OP|＝__________.(2)任意两点P(x1，y1，z1)，Q(x2，y2，z2)间的距离|PQ|＝______________________________.知识点 3空间两点间的距离公式关键能力 · 攻重难典例1[规律方法]　确定点的坐标的方法1．建立空间直角坐标系的原则(1)让尽可能多的点落在坐标轴上或坐标平面内；(2)充分利用几何图形的对称性．2．求某点的坐标时，一般先找出这一点在某一坐标平面上的射影，确定其两个坐标，再找出它在另一轴上的射影(或者通过它到这个坐标平面的距离加上正负号)，确定第三个坐标．【对点训练】❶ 长方体ABCD－A′B′C′D′如图所示，长，宽，高分别为|AB|＝4 cm，|AD|＝3 cm，|AA′|＝5 cm，点N是线段CC′的中点．分别以AB，AD，AA′所在的直线为x轴、y轴、z轴，以1 cm为单位长，建立空间直角坐标系．(1)求A，B，C，D，A′，B′，C′，D′的坐标；(2)求N的坐标．[解析]　(1)A，B，C，D都在平面xOy内，点的竖坐标都为0，它们在x轴、y轴所组成的直角坐标系中的坐标分别是(0，0)，(4，0)，(4，3)，(0，3)，因此空间坐标分别是A(0，0，0)，B(4，0，0)，C(4，3，0)，D(0，3，0)．A′，B′，C′，D′同在一个垂直于z轴的平面内，这个平面与z轴的交点A′在z轴上的坐标是5，故这四点的z的坐标都是5.从这四点作xOy平面的垂线交xOy平面于A，B，C，D四点，故A′，B′，C′，D′的x，y坐标分别与A，B，C，D相同，由此可知它们的空间坐标分别是A′(0，0，5)，B′(4，0，5)，C′(4，3，5)，D′(0，3，5)．(2)点N是线段CC′的中点，有向线段CN的方向与z轴正方向相同，|CN|＝2.5，因此N的z坐标为2.5，C在xOy平面内的平面坐标为(4，3)，这就是N的x，y坐标，故N的空间坐标为(4，3，2.5)． 在空间直角坐标系中，已知点P(－2，1，4)．(1)求点P关于x轴对称的点的坐标；(2)求点P关于xOy平面对称的点的坐标；(3)求点P关于点M(2，－1，－4)对称的点的坐标．[解析]　(1)由于点P关于x轴对称后，它在x轴的分量不变，在y轴、z轴的分量变为原来的相反数，所以对称点坐标为P1(－2，－1，－4)．典例2(2)由于点P关于xOy平面对称后，它在x轴、y轴的分量不变，在z轴的分量变为原来的相反数，所以对称点坐标为P2(－2，1，－4)．(3)设对称点为P3(x，y，z)，则点M为线段PP3的中点，由中点坐标公式，可得x＝2×2－(－2)＝6，y＝2×(－1)－1＝－3，z＝2×(－4)－4＝－12，所以P3的坐标为(6，－3，－12)．[规律方法]　空间点的对称规律1．口诀：求对称点的问题可以用“关于谁对称，谁保持不变，其余坐标相反”的口诀来记忆．2．任意一点P(x，y，z)，关于原点对称的点是P1(－x，－y，－z)；关于x轴(横轴)对称的点是P2(x，－y，－z)；关于y轴(纵轴)对称的点是P3(－x，y，－z)；关于z轴(竖轴)对称的点是P4(－x，－y，z)；关于xOy平面对称的点是P5(x，y，－z)；关于yOz平面对称的点是P6(－x，y，z)；关于zOx平面对称的点是P7(x，－y，z)．【对点训练】❷ (1)点(1，1，－2)关于yOz平面的对称点的坐标是______________；(2)在空间直角坐标系中，点M(－2，4，－3)在zOx平面上的射影为M′点，则M′关于原点对称点的坐标是__________.[解析]　(1)点(1，1，－2)关于yOz平面的对称点的坐标是(－1，1，－2)．(2)M在zOx平面上的射影为M′(－2，0，－3)，所以M′关于原点对称点的坐标为(2，0，3)．(－1，1，－2)　(2，0，3)　 如图所示，在长方体ABCD－A1B1C1D1中，|AB|＝|AD|＝3，|AA1|＝2，点M在A1C1上，|MC1|＝2|A1M|，点N在D1C上且为D1C的中点，求线段MN的长度．典例3[规律方法]　利用空间两点间的距离公式求线段长度问题的步骤【对点训练】❸ 如图所示，在直三棱柱ABC－A1B1C1中，|C1C|＝|CB|＝|CA|＝2，AC⊥CB，D，E分别是棱AB，B1C1的中点，F是AC的中点，求DE，EF的长度．混淆平面直角坐标系与空间直角坐标系 已知空间中两点A(－3，－1，1)，B(－2，2，3)，在z轴上有一点C，它到A，B两点的距离相等，求点C的坐标．典例4[辨析]　上面解法照搬平面解析几何中的解题思路而出现错误．以目前所学知识只能用两点间的距离公式求解．课堂检测 · 固双基1．点P(－1，2，0)位于 (　　)A．y轴上　　 B．z轴上C．xOy平面上　　 D．xOz平面上[解析]　点P(－1，2，0)在xOy平面上，故选C．C　2．在空间直角坐标系O－xyz中，点(3，4，－5)关于z轴对称的点的坐标是 (　　)A．(－3，－4，5)　　 B．(－3，－4，－5)C．(－3，4，5)　　 D．(3，4，5)[解析]　点(3，4，－5)关于z轴对称的点的坐标是(－3，－4，－5)，故选B．B　3．空间直角坐标系中，点M(2，5，8)关于xOy平面对称的点N的坐标为 (　　)A．(－2，5，8)　　 B．(2，－5，8)C．(2，5，－8)　　 D．(－2，－5，8)[解析]　点M(2，5，8)关于xOy平面对称的点N的坐标为(2，5，－8)．C　－7或13　5．如图所示，在正三棱柱ABC－A1B1C1中，底边长为2，高为4，试建立适当的空间直角坐标系，并写出各顶点的坐标．[解析]　取BC的中点O，连接OA，过OA作OD⊥BC交B1C1于点D，则OA⊥BC，OD⊥平面ABC，所以OA，OB，OD两两垂直，以点O为坐标原点，OA，OB，OD所在直线分别为x轴、y轴、z轴建立空间直角坐标系，如图所示．