中考数学三轮冲刺《方程实际问题》解答题冲刺练习01（含答案）

这是一份中考数学三轮冲刺《方程实际问题》解答题冲刺练习01（含答案），共5页。试卷主要包含了4元，求两次下降的百分率；，5x＋225，解得x=50，5，y2=2等内容，欢迎下载使用。
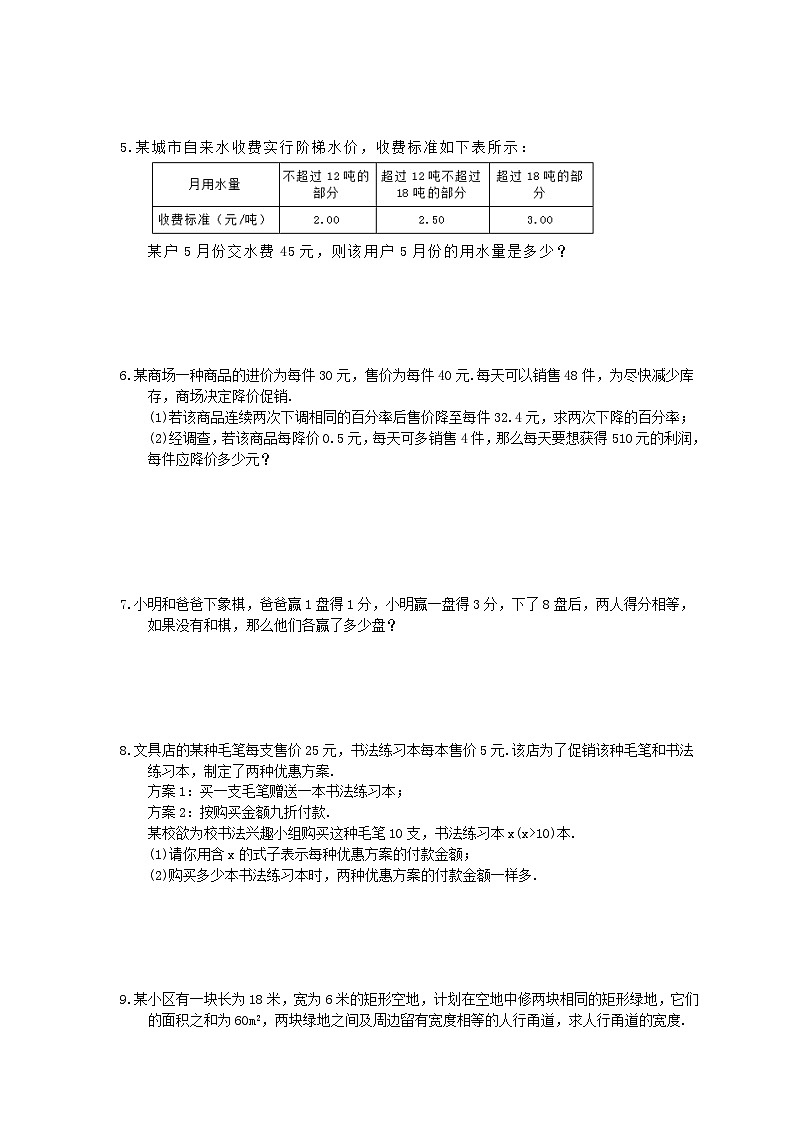
中考数学三轮冲刺《方程实际问题》解答题冲刺练习011.文具店的某种毛笔每支售价25元，书法练习本每本售价5元.该店为了促销该种毛笔和书法练习本，制定了两种优惠方案.方案一：买一支毛笔赠送一本书法练习本；方案二：按购买金额的九折付款.某校欲为校书法兴趣小组购买这种毛笔10支，书法练习本x(x＞10)本.(1)请你用含x的式子表示每种优惠方案的付款金额；(2)购买多少本书法练习本时，两种优惠方案的实际付款数一样多？     2.某景点的门票价格如下：购票人数/人1﹣5051﹣100100人以上每人门票价/元12108我校八年级(1)(2)两个班共102人去游览该景点，其中(1)班人数较少，不到50人，(2)班人数较多，有50多人.如果两班都以班级为单位分别购票.则一共应付1116元；如果两班联合起来作为一个团体购票，则可以节省不少钱，两班各有多少名学生？联合起来购票能省多少钱？     3.某内陆城市为了落实国家“一带一路”倡议，促进经济发展，增强对外贸易的竞争力，把距离港口420 km的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2 h.求汽车原来的平均速度.     4.火车站北广场将于年底投入使用，计划在广场内种植A，B两种花木共6 600棵，若A花木数量是B花木数量的2倍少600棵.(1)A，B两种花木的数量分别是多少棵？(2)如果园林处安排26人同时种植这两种花木，每人每天能种植A花木60棵或B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？     5.某城市自来水收费实行阶梯水价，收费标准如下表所示：某户5月份交水费45元，则该用户5月份的用水量是多少？     6.某商场一种商品的进价为每件30元，售价为每件40元.每天可以销售48件，为尽快减少库存，商场决定降价促销.(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元，求两次下降的百分率；(2)经调查，若该商品每降价0.5元，每天可多销售4件，那么每天要想获得510元的利润，每件应降价多少元？      7.小明和爸爸下象棋，爸爸赢1盘得1分，小明赢一盘得3分，下了8盘后，两人得分相等，如果没有和棋，那么他们各赢了多少盘？     8.文具店的某种毛笔每支售价25元，书法练习本每本售价5元.该店为了促销该种毛笔和书法练习本，制定了两种优惠方案.方案1：买一支毛笔赠送一本书法练习本；方案2：按购买金额九折付款.某校欲为校书法兴趣小组购买这种毛笔10支，书法练习本x(x>10)本.(1)请你用含x的式子表示每种优惠方案的付款金额；(2)购买多少本书法练习本时，两种优惠方案的付款金额一样多.     9.某小区有一块长为18米，宽为6米的矩形空地，计划在空地中修两块相同的矩形绿地，它们的面积之和为60m2，两块绿地之间及周边留有宽度相等的人行甬道，求人行甬道的宽度.     10.某明星演唱会组委会公布的门票价格是：一等席600元；二等席400元；三等席250元.某服装公司在促销活动中组织获前三等奖的36名顾客去观看比赛，计划买两种门票10050元，你能设计几种购买价方案供该公司选择？并说明理由.     
0.中考数学三轮冲刺《方程实际问题》解答题冲刺练习01（含答案）答案解析  一         、解答题1.解：(1)方案一：25×10＋5(x－10)=5x＋200(x＞10)；方案二：(25×10＋5x)×0.9=4.5x＋225(x＞10).(2)由题意，得5x＋200=4.5x＋225，解得x=50.故购买50本书法练习本时，两种优惠方案的实际付款数一样多. 2.解：设(1)班有x人，则(2)班有(102﹣x)人，根据题意得：12x+10(102﹣x)=1116，解得：x=48，∴102﹣x=54，∴1116﹣102×8=300(元).答：甲班又48名学生，乙班有54名学生，联合起来购票能省300元钱. 3.解：设原来的平均速度为x km/h，提高速度后的是(1＋50%)x km/h，由题意得－＝2，解得x＝70，经检验x＝70是原方式方程的根，答：汽车原来的平均速度为70 km/h. 4.解：(1)设B花木数量为x棵，则A花木数量是(2x－600)棵，由题意得x＋2x－600＝6 600，解得x＝2 400，2x－600＝4 200，答：B花木数量为2 400棵，则A花木数量是4 200棵；(2)设安排a人种植A花木，由题意得＝，解得a＝14，经检验，a＝14是原分式方程的解，26－a＝26－14＝12，答：安排14人种植A花木，12人种植B花木. 5.解：如果一个月用水12吨，则需水费12×2=24元，如果一个月用水18吨，则需交水费12×2+6×2.5=39元，5月份交水费45元＞39元，所以5月份，用水量超过了18吨，设用水量为x吨，则12×2+6×2.5+(x﹣18)×3=45，解得x=20，因此，该用户5月份的用水量是20吨. 6.解：(1)设每次降价的百分率为x.40×(1﹣x)2=32.4x=10%或190%(190%不符合题意，舍去)答：该商品连续两次下调相同的百分率后售价降至每件32.4元，两次下降的百分率啊10%；(2)设每天要想获得510元的利润，且更有利于减少库存，则每件商品应降价y元，由题意，得(40﹣30﹣y)(4×+48)=510，解得：y1=1.5，y2=2.5，∵有利于减少库存，∴y=2.5.答：要使商场每月销售这种商品的利润达到510元，且更有利于减少库存，则每件商品应降价2.5元. 7.解：设小明赢了x盘，则爸爸赢了(8－x)盘，根据题意得：3x=8－x，解得：x=2，小明赢了2盘，爸爸赢了6盘. 8.解：(1)方案1：5x＋200(x>10)；方案2：4.5x＋225(x>10).(2)购买50本时，两种方案实际付款一样多. 9.解：设人行道的宽度为x米(0＜x＜3)，根据题意得：
(18-3x)(6-2x)=60，
整理得，(x-1)(x-8)=0.
解得：x1=1，x2=8(不合题意，舍去).
答：人行通道的宽度是1米. 10.解：①设购买一等席x张，二等席(36﹣x)张.根据题意得：600x+400(36﹣x)=10050.解得：x=﹣21.75(不合题意).②设购买一等席x张，三等席(36﹣x)张.根据题意得：600x+250(36﹣x)=10050.解得：x=3.∴可购买一等席3张，二等席位33张.③设购买二等席x张，三等席(36﹣x)张.根据题意得：400x+250(36﹣x)=10050.解得：x=7.∴可购买二等席7张，二等席位29张.答；共有2中方案可供选择，方案①可购买一等席3张，二等席位33张；方案②可购买二等席7张，二等席位29张.