江苏省无锡市四校2022-2023学年高二数学下学期4月期中联考试题（Word版附答案）

这是一份江苏省无锡市四校2022-2023学年高二数学下学期4月期中联考试题（Word版附答案），共11页。试卷主要包含了1B．0，已知，则等内容，欢迎下载使用。
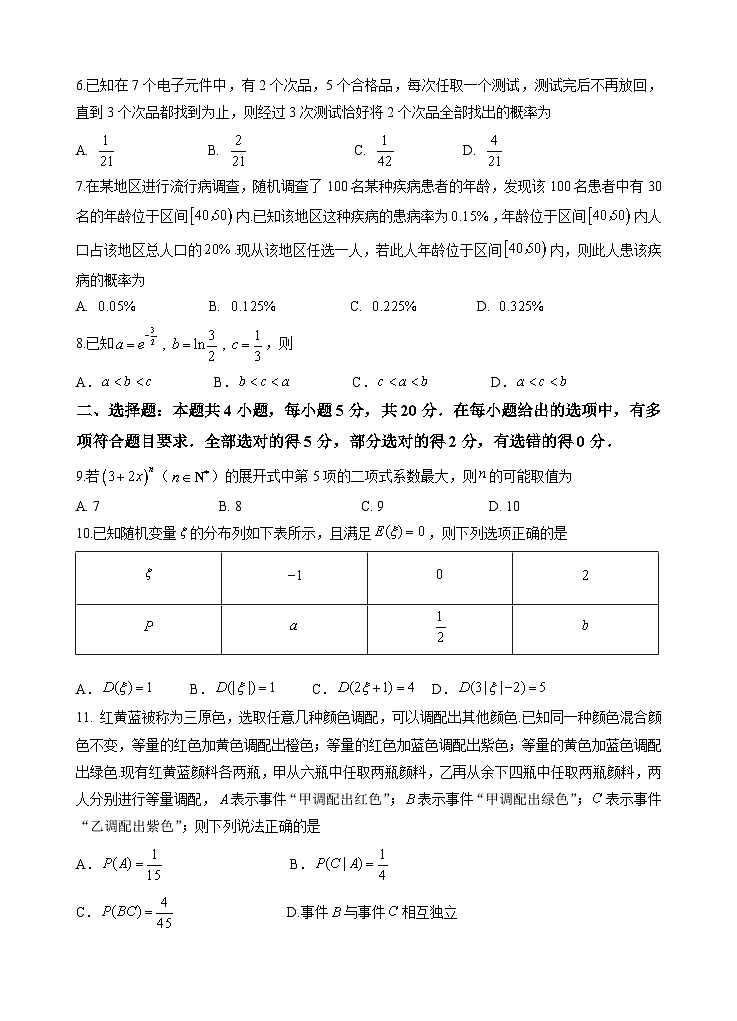
2022-2023学年度春学期四校期中联考试卷高二数学  本试卷共4页，22小题，满分150分.考试用时120分钟.注意事项：1.答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上.2.作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.3.非选择题答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案.不按以上要求作答无效.一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.若，则A. 30             B. 20     C. 12         D. 62.下列求导运算正确的是A.    B.    C.  D. 3.一机械制造加工厂的某条生产线在设备正常运行的情况下，生产的零件尺寸z（单位：）服从正态分布，且，则A．0.1 B．0.04         C．0.05             D．0.064.已知函数与的部分图像如图所示，则A.       B. C.        D. 5.学校有个优秀学生名额，要求分配到高一、高二、高三，每个年级至少个名额，则不同的分配方案种数为A． B．          C．              D．6.已知在7个电子元件中，有2个次品，5个合格品，每次任取一个测试，测试完后不再放回，直到3个次品都找到为止，则经过3次测试恰好将2个次品全部找出的概率为A.              B.                C.           D. 7.在某地区进行流行病调查，随机调查了100名某种疾病患者的年龄，发现该100名患者中有30名的年龄位于区间内.已知该地区这种疾病的患病率为，年龄位于区间内人口占该地区总人口的.现从该地区任选一人，若此人年龄位于区间内，则此人患该疾病的概率为A.           B.           C.         D. 8.已知，则A． B． C． D．二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.若（）的展开式中第5项的二项式系数最大，则的可能取值为A. 7                 B. 8                 C. 9               D. 1010.已知随机变量的分布列如下表所示，且满足，则下列选项正确的是 A．     B．     C．  D．11. 红黄蓝被称为三原色，选取任意几种颜色调配，可以调配出其他颜色.已知同一种颜色混合颜色不变，等量的红色加黄色调配出橙色；等量的红色加蓝色调配出紫色；等量的黄色加蓝色调配出绿色.现有红黄蓝颜料各两瓶，甲从六瓶中任取两瓶颜料，乙再从余下四瓶中任取两瓶颜料，两人分别进行等量调配，表示事件“甲调配出红色”；表示事件“甲调配出绿色”；表示事件“乙调配出紫色”；则下列说法正确的是A．                  B．C．                D.事件与事件相互独立12. 若二次函数的图象与曲线存在公切线，则实数的可能取值为A．          B.             C.              D. 三、填空题：本题共4小题，每小题5分，共20分．请将答案填写在答题卡相应的位置上.13.已知的展开式中含的项的系数为____▲____．14.甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端且甲和乙不相邻，则不同的排列方式有___▲___种.15.已知函数，则在处的切线方程为___▲____．16.某工厂的某种产品成箱包装，每箱100件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品．检验时，先从这箱产品中任取10件作检验，再根据检验结果决定是否对余下的所有产品作检验．设每件产品为不合格品的概率都为，且各件产品是否为不合格品相互独立．记10件产品中恰有3件不合格品的概率为，则取最大值时，____▲____．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）一只口袋中装有形状、大小都相同的10个小球，其中有红球1个，黑球4个，白球5个．（1）从中1次随机摸出3个球，记白球的个数为X，求随机变量X的概率分布；（2）从袋子中任取两个小球，若其中一个小球是黑球，求另一个小球也是黑球的概率.    18.（12分）用0，1，2，3，4这五个数字组成无重复数字的自然数．（1）在组成的五位数中，能被5整除的个数有多少？（2）在组成的五位数中，所有奇数的个数有多少?（3）在组成的五位数中，数字1和3相邻的个数有多少?（4）在组成的五位数中，若从小到大排列，30421排第几个?  19.（12分）已知展开式的二项式系数和为512，且．（1）求的值；（2）求的值；（3）求被6整除的余数．    20.（12分）设函数，其中实数满足．(1)若且在上单调递增，求的取值范围；(2)若，求函数的极值；    21.（12分）水蜜桃是生活中常见的水果之一，适量食用可以增高人体血红蛋白的含量，补充人体的维生素和膳食纤维，但水蜜桃的外皮较薄，往往小的划痕都容易造成它的腐烂变质。某水果批发市场，在水蜜桃成熟以后进行装箱，每一箱10个．根据以往经验，该种水果每箱含有0，1，2个坏果的概率分别为，，．(1)现随机取三箱该水蜜桃，求三箱水蜜桃中坏果总数恰有3个的概率；(2)现随机打开一箱该水蜜桃，并从中任取2个，设X为坏果的个数，求X的分布列及期望．    22.（12分）已知函数，.(1)讨论函数的单调性； (2)若恒成立，求实数的取值范围.
2022-2023学年度春学期四校期中联考试卷高二数学参考答案及评分标准一、选择题：本题共8小题，每小题5分，共40分．1.A  2.D  3.D  4.B  5.C  6.B  7.C  8.D 二、选择题：本题共4小题，每小题5分，共20分．9.BCD  10.ACD  11.AC  12.AC三、填空题：本题共4小题，每小题5分，共20分．13.50    14.36    15.    16.四、解答题：本题共6小题，共70分．17.解：（1）可能的取值为0，1，2，3．，，，，概率分布为0123………………………..5分（概率每个1分，表格1分）（2）设“从袋子中任取两个小球，其中一个小球是黑球”为事件；“另一个小球也是黑球”为事件则     由条件概率公式可得从袋子中任取两个小球，若其中一个小球是黑球，另一个小球也是黑球的概率为…………..10分18.解：（1）能被5整除的个数有个；                       ……………..3分（2）在组成的五位数中，所有奇数的个数有个；      ………..6分（3）在组成的五位数中，数字1和3相邻的个数有个；……..9分（4）（4）比30421小的五位数，若万位为1或2，其余位置任意排，即，若万位为3，比30421小的有5个从小到大排列，30124排第54个.                                .………..12分                                               19.解：（1）因为展开式的二项式系数和为512，所以，解得，                                    ………..2分因为，所以，      ………..4分（2）在中，令，则，令，可得，所以………..7分（3），，因为（）能被6整除，而，即被6整除余数为5，所以被6整除的余数为5                              ………..12分20.解：（1））因为，所以，                   ………..1分故因为在上单调递增，所以在上恒成立，                     ………..3分，所以                                       ………..5分（2）因为，，所以，所以，，令，解得，，                             ………..8分x0—0极大值极小值 所以函数的极大值为，极小值为． ………..12分21.解：（1）三箱水蜜桃中坏果总数恰有3个坏果的情况有：有一箱有2个坏果，一箱有1个坏果，另外一箱没有坏果，或者三箱各有一个坏果，三箱水果中坏果总数恰有3个坏果的概率为………………………..4分（2）由题意可知：可取0,1,2则 ,,,所以的分布列为：012………………………..9分（一个概率1分，列表没有扣2分）期望为………………………..12分22.解：（1）的定义域为，当时，恒成立，所以在上单调递减；当时，令解得，所以在上单调递增；令解得，所以在上单调递减，综上所述：当时，在上单调递减；                ………..3分当时，在上单调递增，在上单调递减；（2）在恒成立化简得                                        ………..4分法一：令，定义域为，.①当时，单调递增，的值域为R，不符合题意；②当时，，也不符合题意；                    ………..5分③当时，令，则 恒成立，所以在上单调递增.当时，，又，根据零点存在定理以及函数的单调性可知，有，即有唯一解，有，此时；（零点未找扣两分）                   ………..8分当时，，又，根据零点存在定理以及函数的单调性可知，有，即有唯一解，有，此时.综上所述，对，都有唯一解，有，此时.又当时，，即，所以在上单调递减；当时，，即，所以在上单调递增.所以，故只需.                                             ………..10分令，上式即转化为，设，则.当时，，所以在上单调递增；当时，，所以在上单调递减.所以，当时，有最大值，所以，所以.又，所以，所以.由，解得．综上所述                                                  ………..12分法二：恒成立令故在上单调递增，所以问题转化为在恒成立                     ………..6分设，当时，恒成立，在上单调递增，又所以时，，不符合题意；                  ………..7分当时，在上单调递减，上单调递增，所以，当时，都有均不符合题意，当时，，此时在恒成立     ………..11分综上所述：                                            ………..12分（直接猜对答案给1分）