2022-2023学年湖南省长沙市长郡教育集团七年级（下）期中数学试卷（含解析）

这是一份2022-2023学年湖南省长沙市长郡教育集团七年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
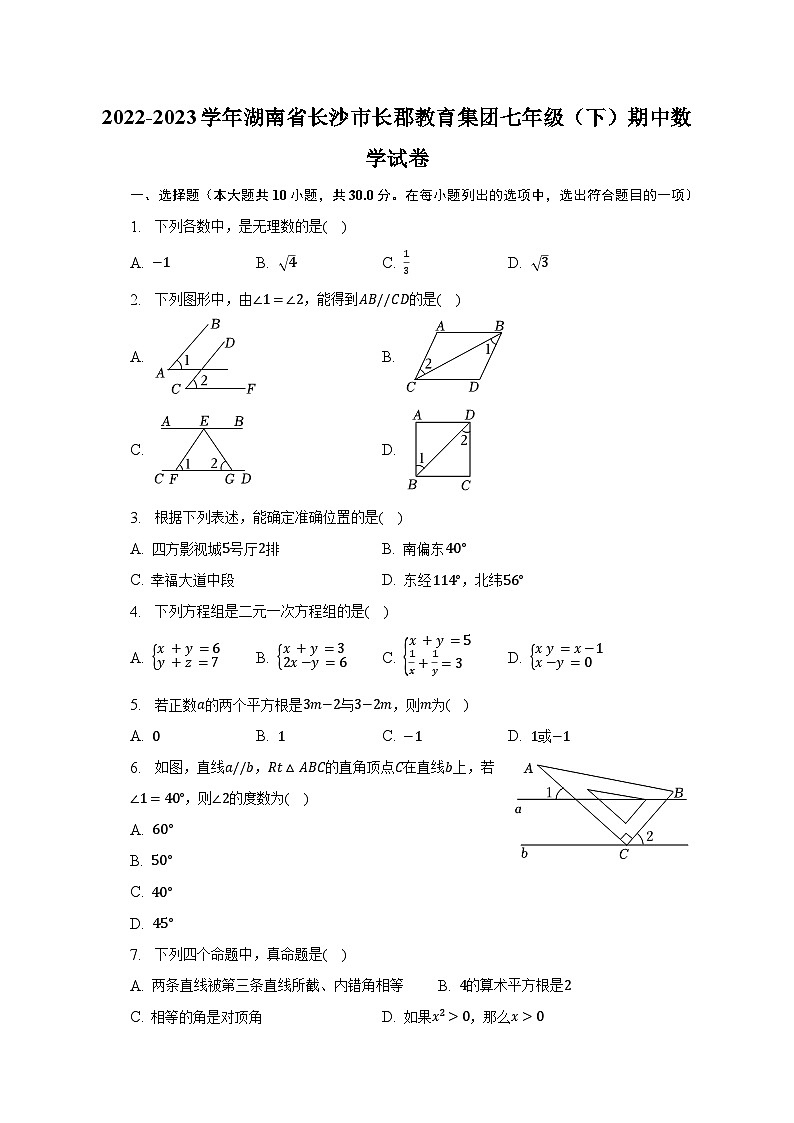
2022-2023学年湖南省长沙市长郡教育集团七年级（下）期中数学试卷一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）1.  下列各数中，是无理数的是(    )A.  B.  C.  D. 2.  下列图形中，由，能得到的是(    )A.  B.
C.  D. 3.  根据下列表述，能确定准确位置的是(    )A. 四方影视城号厅排 B. 南偏东
C. 幸福大道中段 D. 东经，北纬4.  下列方程组是二元一次方程组的是(    )A.  B.  C.  D. 5.  若正数的两个平方根是与，则为(    )A.  B.  C.  D. 或6.  如图，直线，的直角顶点在直线上，若，则的度数为(    )A.
B.
C.
D. 7.  下列四个命题中，真命题是(    )A. 两条直线被第三条直线所截、内错角相等 B. 的算术平方根是
C. 相等的角是对顶角 D. 如果，那么8.  如图，将沿方向平移得到，若的周长为，则四边形的周长为(    )A.
B.
C.
D. 9.  若，是方程的两个解，则的值为(    )A.  B.  C.  D. 10.  如图，动点在平面直角坐标系中按图中符头所示方向运动，第一次从原点运动到点，第二次运动到点，第三次运动到，，按这样的运动规律，第次运动后、动点的坐标是(    )
A.  B.  C.  D. 二、填空题（本大题共6小题，共18.0分）11.  我们知道魔方可以看作是一个正方体，如图，有一个体积为的魔方，则魔方的棱长为______ ．
 12.  已知点，则点到轴的距离为______．13.  若实数，满足，则的值是______ ．14.  已知点在第四象限且，请写出一个符合条件的点坐标：______ ．15.  物理中有一种现象，叫折射现象，它指的是当光线从空气射入水中时，光线的传播方向会发生改变如图，我们建立折射现象数学模型，表示水面，它与底面平行，光线从空气射入水里时发生了折射，变成光线射到水底处，射线是光线的延长线，，，则的度数为______ 16.  如图，把两个形状和大小都一样的小长方形边框厚度忽略不计摆成形，已知，，则一个小长方形面积为______ ．
 三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）17.  本小题分
计算．
；
．18.  本小题分
解方程组．
；
．19.  本小题分
如图，平面直角坐标系中，点为坐标原点，已知三个顶点坐标分别为，，将向左平移个单位得到，点，，的对应点分别是，，．
请在图中画出；
求的面积；
若且轴，则点的坐标为______ ．
20.  本小题分
在解方程组时，由于粗心，甲看错了方程组中的，而得解为；乙看错了方程组中的，而得解为，求的平方根．21.  本小题分
如图，已知直线分别交射线，于点，，连接和，，试说明：．
已知，
______ ，
______ ，
______ ______ ，
______ ______ ，
______ 两直线平行，同旁内角互补，
______ ，对顶角相等，
．
22.  本小题分
已知：如图，，平分，平分．
求证：；
若，，求的度数．
23.  本小题分
某店准备促销“种盲盒”和“种盲盒”，已知“种盲盒”的成本为元个，售价为元个，“种盲盒”的成本为元个，售价为元个，第一天销售这两种盲盒共个，获利元．
求第一天这两种盲盒的销量分别是多少个；
经过第一天的销售后，这两种盲盒的库存发生了变化，为了更好的销售这两种盲盒，店主决定把“种盲盒”的售价在原来的基础上增加元，“种盲盒”的售价在原来的基础上减少元，“种盲盒”的销量在原来的基础上减少了个，“种盲盒”的销量在原来的基础上增加了个，但两种盲盒的成本不变，结果获利比第一天多元求的值．24.  本小题分
规定：若是以，为未知数的二元一次方程的正整数解，则称此时点为二元一次方程的“郡园点”请回答以下关于，的二元一次方程的相关问题．
方程的“郡园点”的坐标为______ ．
已知，为非负整数，且，若是方程的“郡园点”，求的值；
“郡园点”满足关系式：，其中为整数，求“郡园点”的坐标．25.  本小题分
如图，在长方形中，为平面直角坐标系的原点，，，点在第一象限．

点的坐标为______ ；
如图，点是线段延长线上的点，连接，，则，，三个角满足的关系是什么？并说明理由；
在的基础上，已知：，，在第一象限内取一点，连接，，满足，，请直接写出的值．
答案和解析 1.【答案】 【解析】解：是整数，属于有理数，故本选项不合题意；
B.，是整数，属于有理数，故本选项不合题意；
C.是分数，属于有理数，故本选项不合题意；
D.是无理数，故本选项符合题意．
故选：．
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
本题考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽得到的数；以及两个之间依次多一个，等有这样规律的数．
 2.【答案】 【解析】解：由，不能得到，故此选项不符合题意；
B.由，可以得到，不能得到，故此选项不符合题意；
C.由，不能得到，故此选项不符合题意；
D.由，能得到，故此选项符合题意；
故选：．
根据平行线的判定定理逐一判断即可得出答案．
本题考查了平行线的判定，熟练掌握判定定理是解题的关键．
 3.【答案】 【解析】解：、四方影视城号厅排，不能确定具体位置，不符合题意；
B、南偏东，不能确定具体位置，不符合题意；
C、幸福大道中段，不能确定具体位置，不符合题意；
D、东经，北纬，可以确定具体位置，符合题意；
故选：．
根据确定位置需要两个数据进行逐一分析即可．
本题主要考查了确定位置，解决本题的关键是理解确定位置的方法．
 4.【答案】 【解析】解：、有三个未知数，不是二元一次方程组，故A错误，不合题意；
B、有两个未知数，且次数为一次，故B正确，符合题意；
C、含有未知数项和的次数不是，因此不是二元一次方程组，故C错误，不合题意；
D、含有未知数项的次数为，因此不是二元一次方程组，故D错误，不合题意．
故选：．
根据二元一次方程组的定义进行判断即可．
本题考查二元一次方程组的判断，解题的关键是熟记二元一次方程组的定义，如果方程组中含有两个未知数，且含未知数项的次数都是一次，那么这样的方程组叫做二元一次方程组．
 5.【答案】 【解析】解：正数的两个平方根是与，
，
解得：，
故选：．
根据一个正数有两个平方根，它们互为相反数即可求解．
本题主要考查了平方根，掌握平方根的性质是解题的关键．
 6.【答案】 【解析】解：如图

，
，
．
故选：．
根据可知，再由平角可知．
本题考查平行线的性质，解题关键是结合图形利用平行线的性质进行角的转化和计算．
 7.【答案】 【解析】解：、两条平行线被第三条直线所截，内错角相等，故错误，为假命题；
B、的算术平方根是，故正确，为真命题；
C、相等的角不一定是对顶角，故错误，为假命题；
D、如果，那么，故错误，为假命题．
故选：．
利用平行线的性质，算术平方根，对顶角等知识分别判断后即可确定正确的选项．
本题考查了命题与定理的知识，解题的关键是了解平行线的性质，算术平方根，对顶角，属于基础知识，难度不大．
 8.【答案】 【解析】解：沿方向平移得到，
，，
的周长为，
，
四边形的周长．
故选：．
先根据平移的性质得到，，再利用三角形周长的定义得到，然后利用等线段代换得到四边形的周长．
本题考查平移的性质：平移不改变图形的形状和大小；经过平移，对应点所连的线段平行或共线且相等，对应线段平行且相等，对应角相等．
 9.【答案】 【解析】解：，是方程的两个解，
，．
，．
．
故选：．
根据方程的解的定义，得，，故，，进而求得．
本题主要考查方程的解的定义以及解二元一次方程组，熟练掌握方程的解的定义以及解二元一次方程组是解决本题的关键．
 10.【答案】 【解析】解：由图形可得，，，，，，
横坐标依次加，纵坐标，，，，，循环，循环周期为，
，
是第个周期后的第个，
，
故选：．
根据点坐标的循环规律计算求值即可．
本题考查了平面直角坐标系坐标规律的探索，由图形找出纵坐标的循环周期是解题关键．
 11.【答案】 【解析】解：根据题意得，设正方体的棱长为，
，则，
正方体的棱长为，
故答案为：．
正方体的体积是棱长的三次幂，已知体积求棱长，则是求体积的三次方根，由此即可求解．
本题主要考查求一个数的立方根，掌握立方根的概念和求一个数的立方根是解题的关键．
 12.【答案】 【解析】解：点到轴的距离为．
故答案为：．
根据点到轴的距离等于横坐标的绝对值解答．
本题考查了点的坐标，是基础题，熟记点到轴的距离等于横坐标的绝对值是解题的关键．
 13.【答案】 【解析】解：根据题意得：，
解得：，
则．
故答案为：．
首先根据非负数的性质可求出、的值，进而可求出、的和．
本题考查了非负数的性质：有限个非负数的和为零，那么每一个加数也必为零．
 14.【答案】 【解析】解：点在第四象限，
，，
，
，
故答案为：答案不唯一．
根据第四象限内坐标的特征，结合横纵坐标互为相反数可得结果．
本题考查了点的坐标，解题的关键是掌握个象限内点的坐标特征．
 15.【答案】 【解析】解：，
．
，
．
故答案为：．
由平行线的性质可知，再根据对顶角相等得出，最后由求解即可．
本题考查平行线的性质、对顶角相等等知识点，掌握平行线的性质是解题的关键．
 16.【答案】 【解析】解：设小长方形的长和宽分别为，，
由题意得，，
解得，
长方形的面积为，
故答案为：．
设小长方形的长和宽分别为，，然后根据，列出方程组求出、的值，最后根据长方形面积公式进行求解即可．
本题主要考查了二元一次方程组的实际应用，正确理解题意列出方程组求出小长方形的长和宽是解题的关键．
 17.【答案】解：

；


． 【解析】先算乘方，化简绝对值，再算加减法；
先算开方，再算加减法．
此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
 18.【答案】解：，
得：，
把代入得：，解得，
方程组的解为；
，
得：，解得，
把代入得：，解得，
方程组的解为． 【解析】利用加减消元法解方程组即可．
本题主要考查了解二元一次方程组，熟知加减消元法是解题的关键．
 19.【答案】 【解析】解：如图所示，即为所求；

；
由得，
且轴，
，
，
，
点的坐标为，
故答案为：．
先根据平移分式确定、、对应点、、的坐标，再描出、、，最后顺次连接、、即可；
利用割补法求解即可；
先求出，再根据平行于轴的直线上的点横坐标相同求出的值即可求出点的坐标．
本题主要考查了坐标与图形，坐标与图形变化平移，求三角形面积，灵活运用所学知识是解题的关键．
 20.【答案】解：把代入得：，
解得：，
把代入得：，
解得：，
，
的平方根为． 【解析】把甲的结果代入方程组第二个方程求出的值，把乙的结果代入方程组中第一个方程求出的值，进而确定出方程组的解，代入中计算平方根即可．
此题考查了二元一次方程组的解，平方根，充分理解题意，求出，的值是解本题的关键．
 21.【答案】两直线平行，同位角相等  已知    等量代换    内错角相等，两直线平行     【解析】解：已知，
两直线平行，同位角相等，
已知，
等量代换，
内错角相等，两直线平行，
两直线平行，同旁内角互补，
，对顶角相等，
．
故答案为：两直线平行，同位角相等；已知；；等量代换；；内错角相等，两直线平行；；．
先根据平行线的性质得到，可推出，即可证明，则，再由，，即可证明．
本题主要考查了平行线的性质与判定，熟知平行线的性质与判定条件是解题的关键．
 22.【答案】证明：，
，
平分，平分，
，，
，
；
解：，
，
，，
，
，
解得：，
，
． 【解析】根据平行线的性质得到，根据角平分线的定义得到，，可得，即可证明；
根据垂线的定义得到，利用，列出方程，求出，从而得到，最后利用三角形内角和定理计算即可．
本题考查了平行线的判定和性质，角平分线的定义，垂线的定义，三角形内角和，解题的关键是熟练掌握平行线的判定和性质．
 23.【答案】解：设第一天这两种盲盒的销量分别是个，个，
由题意得，，
解得，
第一天这两种盲盒的销量分别是个，个，
答：第一天这两种盲盒的销量分别是个，个；
由题意得，，
，
解得． 【解析】设第一天这两种盲盒的销量分别是个，个，再根据第一天销售这两种盲盒共个，获利元，列出方程组求解即可；
根据利润售价成本数量列出方程求解即可．
本题主要考查了二元一次方程组的实际应用，一元一次方程的实际应用，正确理解题意找到等量关系是解题的关键．
 24.【答案】 【解析】解：，
，
解得：，
即正整数解为，
“郡园点”的坐标为；
是方程的“郡园点”，
，且和是正整数，
，
解得：，，
，为非负整数，
，，
；
，
，
则，
，
由可得：．
求出的正整数解，即可得到结果；
根据题意得到方程组，解之，可得，值，代入计算即可；
根据已知等式，利用算术平方根的性质得到，则有，同可得结果．
本题考查了算术平方根的非负性，二元一次方程的解，点的坐标，理解“郡园点”的意义是解题的关键．
 25.【答案】 【解析】解：在长方形中，，，
点在第一象限，
；
，理由是：
设与交于，
，
，
，
；

当在上方时，
，
，
，
，即，
，
，，
，
，
同可得：，即，
，
；

当在下方时，，，，
，
，
，
，
，
．

综上：的值为或．
根据长方形求出各边长，从而得到点坐标；
设与交于，根据平行线的性质得到，再利用外角的性质求解；
分当在上方时和当在下方时，求出相应角的度数，可得结果．
本题考查了坐标与图形，角平分线的定义，平行线的性质，三角形外角的性质，解题的关键是分类讨论，理清角的关系．