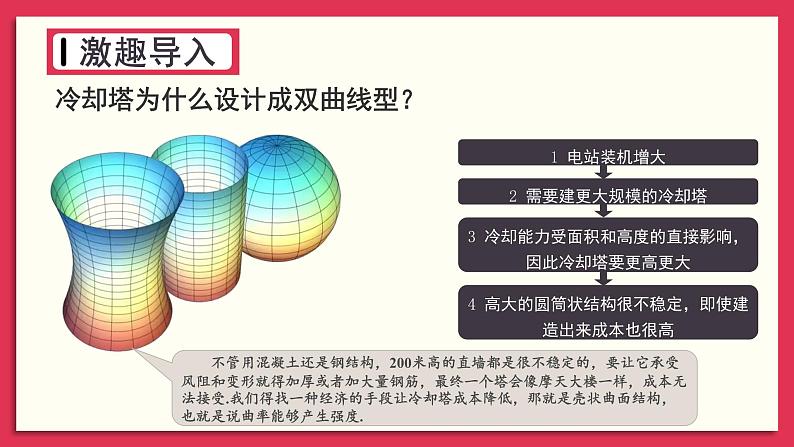
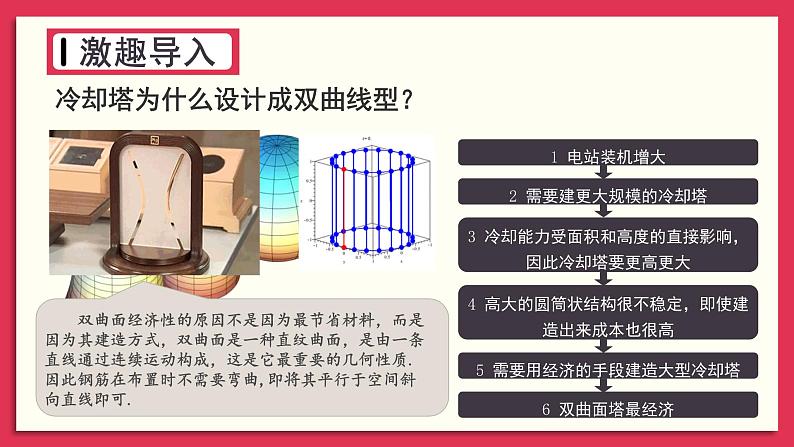
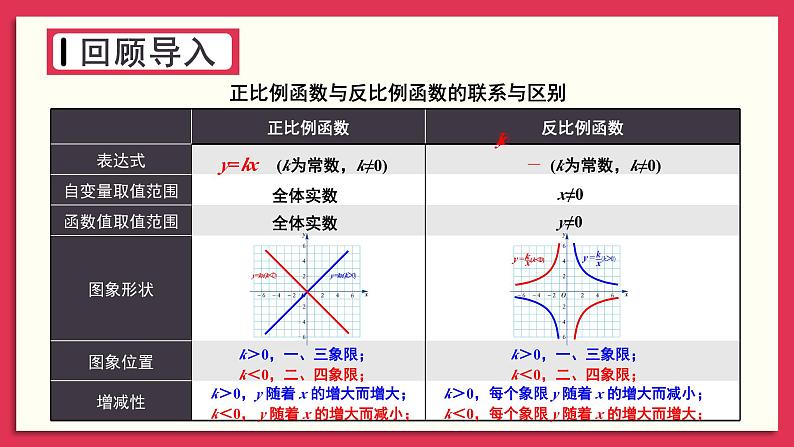
湘教版九年级上册1.1 反比例函数精品教学课件ppt

第3课时 反比例函数的图象与性质的综合应用

【知识与技能】

1.会求反比例函数的表达式；

2.综合运用一次函数和反比例函数的知识解决有关问题；

3.借助一次函数和反比例函数的图象解决某些简单的实际问题．

【过程与方法】

经历观察、分析、交流的过程，逐步提高运用知识的能力.

【情感态度】

能灵活运用函数图象和性质解决一些较综合的问题，培养学生看图（象）、识图（象）能力、体会用“数、形”结合思想解答函数题.

【教学重点】

1.会用待定系数法求反比例函数的表达式；

2.理解并掌握一次函数，反比例函数的图象和性质，并能利用它们解决一些综合问题.

【教学难点】

学会从图象上分析、解决问题，理解反比例函数的性质.

一、情境导入，初步认识

1.正比例函数有哪些性质？

2.一次函数有哪些性质？

3.反比例函数有哪些性质？

4.我们学会了根据函数表达式画函数图象，那么你能根据一些条件求反比例函数的表达式吗？

【教学说明】对所学的三种函数的性质教学复习，让学生对它们的性质有系统的了解.

二、思考探究，获取新知

1.思考：已知反比例函数的图象经过点P（2,4）

（1）求k的值，并写出该函数的表达式；

（2）判断点A（-2，-4），B(3，5)是否在这个函数的图象上；

（3）这个函数的图象位于哪些象限？在每个象限内，函数值y随自变量x的增大如何变化？

分析： (1)题中已知图象经过点P（2，4），即表明把P点坐标代入解析式成立，这样能求出k，解析式也就确定了.

(2)要判断A、B是否在这条函数图象上，就是把A、B的坐标代入函数解析式中，如能使解析式成立，则这个点就在函数图象上.否则不在.

(3)根据k的正负性，利用反比例函数的性质来判定函数图象所在的象限、y随x的值的变化情况.

【归纳结论】这种求解析式的方法叫做待定系数法求解析式.

2.已知一个正比例函数与一个反比例函数的图象交于P（-3,4），试求出它们的表达式，并在同一坐标系内画出这两个函数的图象.

解：设正比例函数，反比例函数的表达式分别为y=k1x，，其中，k1，k2是常数，且均不为0.

由于这两个函数的图象交于P（-3,4），则P（-3,4）是这两个函数图象上的点，即点P的坐标分别满足这两个表达式.

因此，

解得，

所以，正比例函数解析式为，反比例函数解析式为.

函数图象如下图.

【教学说明】通过图象，让学生掌握一次函数与反比例函数的综合应用.

3.在反比例函数的图象上取两点P（1，6），Q（6，1），过点P分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为S1=_______；过点Q分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为S2=_______；S1与S2有什么关系？为什么？

【归纳结论】反比例函数（k≠0）中比例系数k的几何意义：过双曲线（k≠0）上任意一点引x轴、y轴的平行线，与坐标轴围成的矩形面积为k的绝对值.

【教学说明】引导学生根据一定的分类标准研究反比例函数的性质，同时鼓励学生用自己的语言进行表述，从而提高学生的表达能力与数学语言的组织能力．

三、运用新知，深化理解

1.已知如图，A是反比例函数的图象上的一点，AB丄x轴于点B，且△ABO的面积是3，则k的值是（    ）

A.3           B.-3           C.6           D.-6

分析：过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S＝．

解：根据题意可知：S△AOB＝＝3，

又反比例函数的图象位于第一象限，k＞0，

则k＝6．

【答案】 C

2.反比例函数与在第一象限的图象如图所示，作一条平行于x轴的直线分别交双曲线于A、B两点，连接OA、OB，则△AOB的面积为（     ）

A.           B.2           C.3           D.1

分析：分别过A、B作x轴的垂线，垂足分别为D、E，过B作BC⊥y轴，点C为垂足，再根据反比例函数系数k的几何意义分别求出四边形OEAC、△AOE、△BOC的面积，进而可得出结论．

解：分别过A、B作x轴的垂线，垂足分别为D、E，过B作BC⊥y轴，点C为垂足，

∵由反比例函数系数k的几何意义可知，S四边形OEAC=6，S△AOE=3，S△BOC=1，

∴S△AOB=S四边形OEAC-S△AOE-S△BOC=6-3-1=2．

【答案】 B

3.已知点P(2，2)在反比例函数 (k≠0)的图象上，

(1)当x=-3时，求y的值；

(2)当1＜x＜3时，求y的取值范围．

解： （1）∵点P（2，2）在反比例函数的图象上，

∴2=，即k=4，

∴反比例函数的解析式为．

∴当x=-3时，y=．

（2）∵当x=1时，y=4；当x=3时，y=，

又反比例函数在x＞0时y值随x值的增大而减小，

∴当1＜x＜3时，y的取值范围为＜y＜4．

4.已知直线y＝x＋b经过点A(3,0)，并与双曲线的交点为B(-2，m)和C，求k、b的值．

解：点A(3,0)在直线y＝x＋b上，所以0＝3＋b，b＝-3．

一次函数的解析式为：y＝x-3．

又因为点B(-2，m)也在直线y＝x-3上，所以m＝-2-3＝-5，即B(-2,-5)．

而点B(-2,-5)又在反比例函数上，所以k＝-2×(-5)＝10．

5.已知反比例函数的图象与一次函数y＝k2x-1的图象交于A(2,1)．

(1)分别求出这两个函数的解析式；

(2)试判断A点关于坐标原点的对称点与两个函数图象的关系．

分析: (1)因为点A在反比例函数和一次函数的图象上，把A点的坐标代入这两个解析式即可求出k1、k2的值．

(2)把点A关于坐标原点的对称点A′坐标代入一次函数和反比例函数解析式中，可知A′是否在这两个函数图象上．

解：(1)因为点A(2,1)在反比例函数和一次函数的图象上，所以k1＝2×1＝2．

1＝2k2-1，k2＝1．

所以反比例函数的解析式为：；一次函数解析式为：y＝x-1．

(2)点A(2,1)关于坐标原点的对称点是A′(-2,-1)．

把A′点的横坐标代入反比例函数解析式得，，所以点A在反比例函数图象上．

把A′点的横坐标代入一次函数解析式得，y＝-2-1＝-3，所以点A′不在一次函数图象上．

6.如图，一次函数y＝kx＋b的图象与反比例函数的图象交于A、B两点．

(1)利用图象中的条件，求反比例函数和一次函数的解析式；

(2)根据图象写出使一次函数的值大于反比例函数值的x的取值范围．

分析: (1)把A、B两点坐标代入两解析式，即可求得一次函数和反比例函数解析式．

(2)因为图象上每一点的纵坐标与函数值是相对应的，一次函数值大于反比例函数值，反映在图象上，自变量取相同的值时，一次函数图象上点的纵坐标大于反比例函数图象上点的纵坐标．

解∶(1)观察图象可知，反比例函数的图象过点A(-2,1)，m＝-2×1＝-2．

所以反比例函数的解析式为：．又点B(1,a)也在反比例函数图象上，a=．即B(1,-2)．

因为一次函数图象过点A、B．所以解得，

一次函数解析式为：y＝-x-1．

(2)观察图象可知，当x＜-2或0＜x＜1时，一次函数的值大于反比例函数值.

【教学说明】检测题采取多种形式呈现，增加了灵活性，以基础题为主，也有少量综合问题，可使不同层次水平的学生均有机会获得成功的体验．

四、师生互动，课堂小结

先小组内交流收获和感想，而后以小组为单位派代表进行总结.教师作以补充.

布置作业：教材“习题1.2”中第6题.

教学中，我深深地体会到：要想让学生真正掌握求函数解析式的方法，教师应在给出相应的典型例题的条件下，让学生自己去寻找答案，自己去发现规律.最后，教师清楚地向学生总结每一种函数解析式的适用范围，以及一般应告知的条件.在信息社会飞速发展的今天，教师要从以前的教师教、学生学的观念中解放出来，教会学生如何学，让学生自己去探究，自己去学习，去获取知识.在《中学数学课程标准》中明确规定：教师不仅是学生的引导者，也是学生的合作者.教学中，要让学生通过自主讨论、交流，来探究学习中碰到的问题、难题，教师从中点拨、引导，并和学生一起学习，探讨，才能真正做到教学相长，也才能真正让每一个学生都学有所获.