数学冀教版八年级下第二十二章测试题

第二十二章 四边形

(100分，90分钟)

一、选择题(每题2分，共32分)

1．在▱ABCD中，下列结论一定正确的是(　　)

A．AC⊥BD  B．∠A＋∠B＝180°  C．AB＝AD  D．∠A≠∠C

2．顺次连接平行四边形各边中点所得的四边形是(　　)

A．平行四边形  B．长方形  C．任意四边形  D．正方形

3．已知在四边形ABCD中，AB∥CD，添加下列一个条件后，一定能判定四边形ABCD是平行四边形的是(　　)　

A．AD＝BC  B．AC＝BD  C．AB＝CD  D．∠A＝∠B

4．▱ABCD的四个内角∠A，∠B，∠C，∠D的度数的比可能是(　　)

A．2323  B．3443  C．4432  D．2356

5．一个多边形的每个内角均为108°，则这个多边形是(　　)

A．七边形  B．六边形  C．五边形  D．四边形

6. 如图，在▱ABCD中，已知AD＝12 cm，AB＝ 8 cm，AE平分∠BAD交BC边于点E，则CE的长等于(　　)

A．8 cm  B．6 cm  C．4 cm  D．2 cm

7. 已知菱形ABCD中，对角线AC与BD交于点O，∠BAD＝120°，AC＝4，则该菱形的面积是(　　)

A．16  B．16  C．8  D．8

8．如图，矩形纸片ABCD中，AB＝6 cm，BC＝8 cm，现将其沿AE折叠，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为(　　)

A．6 cm  B．4 cm  C．2 cm  D．1 cm

(第6题)

(第8题)

(第9题)

9．如图，在菱形ABCD中，对角线AC与BD相交于点O，E是BC的中点，AD＝6 cm，则OE的长为(　　)

A．6 cm  B．4 cm  C．3 cm  D．2 cm

10．如图，已知▱ABCD的对角线AC，BD相交于点O，EF经过点O，分别交AD，BC于点E，F，且OE＝4，AB＝5，BC＝9，则四边形ABFE的周长是(　　)

A．13  B．16  C．22  D．18

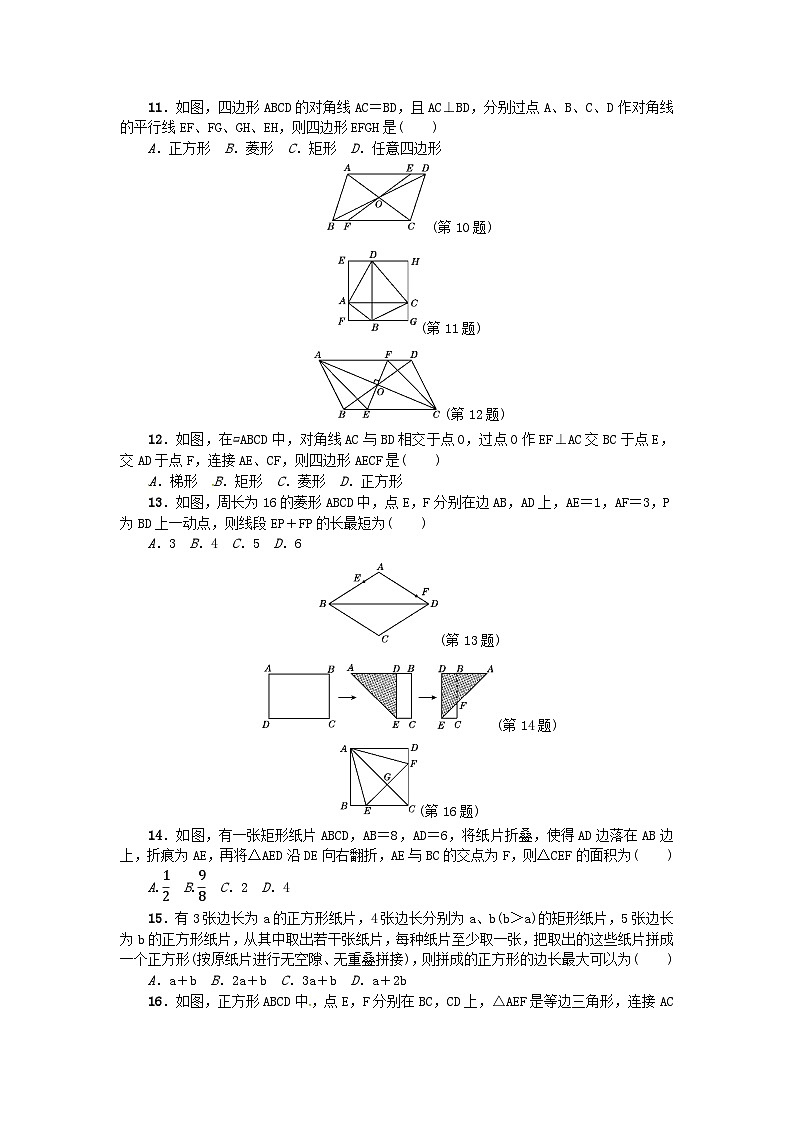
11．如图，四边形ABCD的对角线AC＝BD，且AC⊥BD，分别过点A、B、C、D作对角线的平行线EF、FG、GH、EH，则四边形EFGH是(　　)

A．正方形  B．菱形  C．矩形  D．任意四边形

(第10题)

(第11题)

(第12题)

12．如图，在▱ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF，则四边形AECF是(　　)

A．梯形  B．矩形  C．菱形  D．正方形

13．如图，周长为16的菱形ABCD中，点E，F分别在边AB，AD上，AE＝1，AF＝3，P为BD上一动点，则线段EP＋FP的长最短为(　　)

A．3  B．4  C．5  D．6

(第13题)

(第14题)

(第16题)

14．如图，有一张矩形纸片ABCD，AB＝8，AD＝6，将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为(　　)

A.  B.  C．2  D．4

15．有3张边长为a的正方形纸片，4张边长分别为a、b(b＞a)的矩形纸片，5张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形(按原纸片进行无空隙、无重叠拼接)，则拼成的正方形的边长最大可以为(　　)

A．a＋b  B．2a＋b  C．3a＋b  D．a＋2b

16．如图，正方形ABCD中，点E，F分别在BC，CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE＝DF，②∠DAF＝15°，③AC垂直平分EF，④BE＋DF＝EF，⑤S△CEF＝2S△ABE.其中正确结论有(　　)

A．2个  B．3个  C．4个  D．5个

二、填空题(每题3分，共12分)

17．边数为2 017的多边形的外角和为__________．

18．已知菱形的两条对角线长为12 cm和6 cm，那么这个菱形的面积为________cm2.

(第19题)

19．如图，正方形ABCD的边长为4，E是边BC上的一点且BE＝1，P为对角线AC上的一动点，连接PB，PE，当点P在AC上运动时，△PBE周长的最小值是________．

20．矩形纸片ABCD中，已知AD＝8，AB＝6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为________．

三、解答题(21题8分，25题15分，其余每题11分，共56分)

21．已知：如图，在△ABC中，AB＝AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E.

(1)求证：△ABD≌△CAE；

(2)连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．

(第21题)

22．如图，▱ABCD中，点E，F在直线AC上(点E在F左侧)，BE∥DF.

(1)求证：四边形BEDF是平行四边形；

(2)若AB⊥AC，AB＝4，BC＝2，当四边形BEDF为矩形时，求线段AE的长．

(第22题)

23. 如图，在边长为6的正方形ABCD中，E是边CD的中点，将 △ADE沿AE翻折至△AFE，延长EF交BC于点G，连接AG.

(1)求证：△ABG≌△AFG；

(2)求BG的长．

(第23题)

24．如图，在四边形ABCD中，点E是线段AD上的任意一点(E与A，D不重合)，G，F，H分别为BE，BC，CE的中点．

(1)试说明四边形EGFH是平行四边形；

(2)在(1)的条件下，若EF⊥BC，且EF＝BC，试说明平行四边形EGFH是正方形．

(第24题)

25．如图，已知在Rt△ABC中，∠ACB＝90°，现按如下步骤作图：

①分别以A，C为圆心，a为半径(a＞AC)作弧，两弧分别交于M，N两点；

②过M，N两点作直线MN交AB于点D，交AC于点E；

③将△ADE绕点E顺时针旋转180°，设点D的对应点为点F.

(1)请在图中直接标出点F并连接CF；

(2)求证：四边形BCFD是平行四边形；

(3)当∠B为多少度时，四边形BCFD是菱形？

(第25题)

参考答案：

一、1.B　2.A　3.C

4．A　点拨：平行四边形的对角相等．

5．C　点拨：首先求得一个外角的度数，然后用360°除以一个外角的度数即可得到答案．

6．C　7.C

8．C　点拨：根据折叠的特点可得∠AB1E＝∠B＝90°，AB1＝AB，易知∠BAB1＝90°，然后得出四边形ABEB1是正方形．再根据正方形的性质可得BE＝AB，最后根据CE＝BC－BE，代入数据进行计算即可得解．

9．C　10.C

11．A　点拨：∵EF∥BD，GH∥BD，

∴EF∥GH，同理可得EH∥FG，∴四边形EFGH是平行四边形，∴EH＝FG，EF＝HG.易证四边形EACH和四边形EFBD是平行四边形，∴EH＝AC，EF＝BD.∵AC＝BD，∴EH＝AC＝FG＝EF＝BD＝HG，∴四边形EFGH是菱形．∵AC⊥BD，AC∥EH，EF∥BD，∴EH⊥EF，∴∠E＝90°，∴四边形EFGH是正方形．

12．C　点拨：首先利用平行四边形的性质得出AO＝CO，AD∥BC，所以∠AFO＝∠CEO，又∠AOF＝∠COE，所以△AFO≌△CEO，所以FO＝EO.最后利用平行四边形和菱形的判定定理得出结论．

13．B　点拨：∵四边形ABCD为菱形，

(第13题)

∴AD＝16÷4＝4.

如图，在DC上截取DG＝FD＝AD－AF＝4－3＝1，连接EG，则EG与BD的交点就是点P.

∵AE＝DG，且AE∥DG，

∴四边形ADGE是平行四边形，

∴EG＝AD＝4.

故选B.

14．C

15．D　点拨：3张边长为a的正方形纸片的面积为3a2，4张边长分别为a，b的矩形纸片的面积为4ab，5张边长为b的正方形纸片的面积为5b2.

∵a2＋4ab＋4b2＝(a＋2b)2，∴拼成的正方形的边长最大可以为a＋2b.

16．C　点拨：∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD，

∠B＝∠BCD＝∠D＝∠BAD＝90°.

∵△AEF是等边三角形，

∴AE＝EF＝AF，∠EAF＝60°.

∴∠BAE＋∠DAF＝30°.

在Rt△ABE和Rt△ADF中，

∴Rt△ABE≌Rt△ADF(HL)，

∴BE＝DF(故①正确)．

易知∠BAE＝∠DAF.

∴∠DAF＋∠DAF＝30°，即∠DAF＝15°(故②正确)．

∵BC＝CD，∴BC－BE＝CD－DF，即CE＝CF，

又∵AE＝AF，

∴AC垂直平分EF(故③正确)．

设EC＝x，由勾股定理，得EF＝AE＝x，∴EG＝CG＝x，∴AG＝x，

∴AC＝，

∴AB＝BC＝，

∴BE＝－x＝，

∴BE＋DF＝x－x≠x(故④错误)．

∵S△CEF＝，

S△ABE＝＝，

∴2S△ABE＝＝S△CEF(故⑤正确)．综上所述，正确的有4个．

二、17.360°

18．36　点拨：菱形的面积为×12×6＝36(cm2)．

19．6

20．3或6　点拨：①∠EFC＝90°时，如图①，先判断出点F在对角线AC上，利用勾股定理列式求出AC，设BE＝x，表示出CE，根据翻折变换的性质可得AF＝AB，EF＝BE，然后在Rt△CEF中，利用勾股定理列出方程求解即可；②∠CEF＝90°时，如图②，判断出四边形ABEF是正方形，根据正方形的四条边都相等可得BE＝AB.

(第20题)

三、21.(1)证明：∵AB＝AC，

∴∠B＝∠ACB.

又∵AD是BC边上的中线，

∴AD⊥BC，即∠ADB＝90°.

∵AE∥BC，∴∠EAC＝∠ACB，

∴∠B＝∠EAC.

∵CE⊥AE，∴∠CEA＝90°，

∴∠CEA＝∠ADB.

又AB＝AC，

∴△ABD≌△CAE(AAS)．

(2)解：AB∥DE且AB＝DE.

证明如下：由(1)中△ABD≌△CAE可得AE＝BD，

又∵AE∥BD，∴四边形ABDE是平行四边形．

∴AB∥DE且AB＝DE.

22．(1)证明：如图，连接BD，设BD交AC于点O.

∵四边形ABCD是平行四边形，

∴OB＝OD.

由BE∥DF，得∠BEO＝∠DFO.而∠EOB＝∠FOD，

∴△BEO≌△DFO.

∴BE＝DF.又∵BE∥DF，

∴四边形BEDF是平行四边形．

(2)解：∵AB⊥AC，AB＝4，BC＝2，∴AC＝6，AO＝3.

∴在Rt△BAO中，

BO＝＝＝5.

又∵四边形BEDF是矩形，

∴OE＝OB＝5.

∴点E在OA的延长线上，且AE＝2.

(第22题)

23．(1)证明：∵四边形ABCD是正方形，∴∠B＝∠D＝90°，AD＝AB.

由折叠的性质可知，AD＝AF，

∠AFE＝∠D＝90°，

∴∠AFG＝90°，AB＝AF.

又∵AG＝AG，

∴Rt△ABG≌Rt△AFG(HL)．

(2)解：∵△ABG≌△AFG，

∴BG＝FG.

设BG＝FG＝x，则GC＝6－x，

∵E为CD的中点，

∴CE＝EF＝DE＝3，

∴EG＝x＋3.

在Rt△CEG中，由勾股定理，得32＋(6－x)2＝(x＋3)2，解得x＝2，

∴BG＝2.

24．解：(1)在△BEC中，

∵G，F分别是BE，BC的中点，

∴GF∥EC(即GF∥EH)且GF＝EC.

∵H为EC的中点，∴EH＝EC，

∴GF＝EH.

∴四边形EGFH是平行四边形．

(2)连接GH.∵G，H分别是BE，CE的中点，∴GH∥BC且GH＝BC，又∵EF⊥BC且EF＝BC，∴EF⊥GH且EF＝GH.∴平行四边形EGFH是正方形．

25．(1)解：如图所示．

(2)证明：连接AF，DC.

∵△CFE是由△ADE顺时针旋转180°后得到的，A与C是对应点，D与F是对应点，

∴AE＝CE，DE＝FE.

∴四边形ADCF是平行四边形．

∴AD∥CF.

由作图可知MN垂直平分AC，

又∵∠ACB＝90°，

∴MN∥BC.

∴四边形BCFD是平行四边形．

(第25题)

(3)解：当∠B＝60°时，四边形BCFD是菱形．理由如下：

∵∠B＝60°，∠ACB＝90°，

∴∠BAC＝30°.∴BC＝AB.

又易知BD＝AB，

∴BD＝BC.

∵四边形BCFD是平行四边形，

∴四边形BCFD是菱形．