

2018年内蒙古赤峰市中考数学试卷(解析版)
展开2018年内蒙古赤峰市中考数学试卷
一、选择题(每小题给出的选项中只有一个符合题意,请将符合题意的选项序号,在答题卡的对应位置上按要求涂黑.每小题3分,共计36分)
1.|(﹣3)﹣5|等于( )
A.﹣8 B.﹣2 C.2 D.8
2.下列图形中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.风景秀美的赤峰有“草原明珠”的美称,赤峰市全域总面积为90021平方公里.90021用科学记数法表示为( )
A.9.0021×105 B.9.0021×104 C.90.021×103 D.900.21×102
4.下列运算正确的是( )
A.3x+2y=5(x+y) B.x+x3=x4 C.x2•x3=x6 D.(x2)3=x6
5.直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )
A.65° B.50° C.55° D.60°
6.能使式子+成立的x的取值范围是( )
A.x≥1 B.x≥2 C.1≤x≤2 D.x≤2
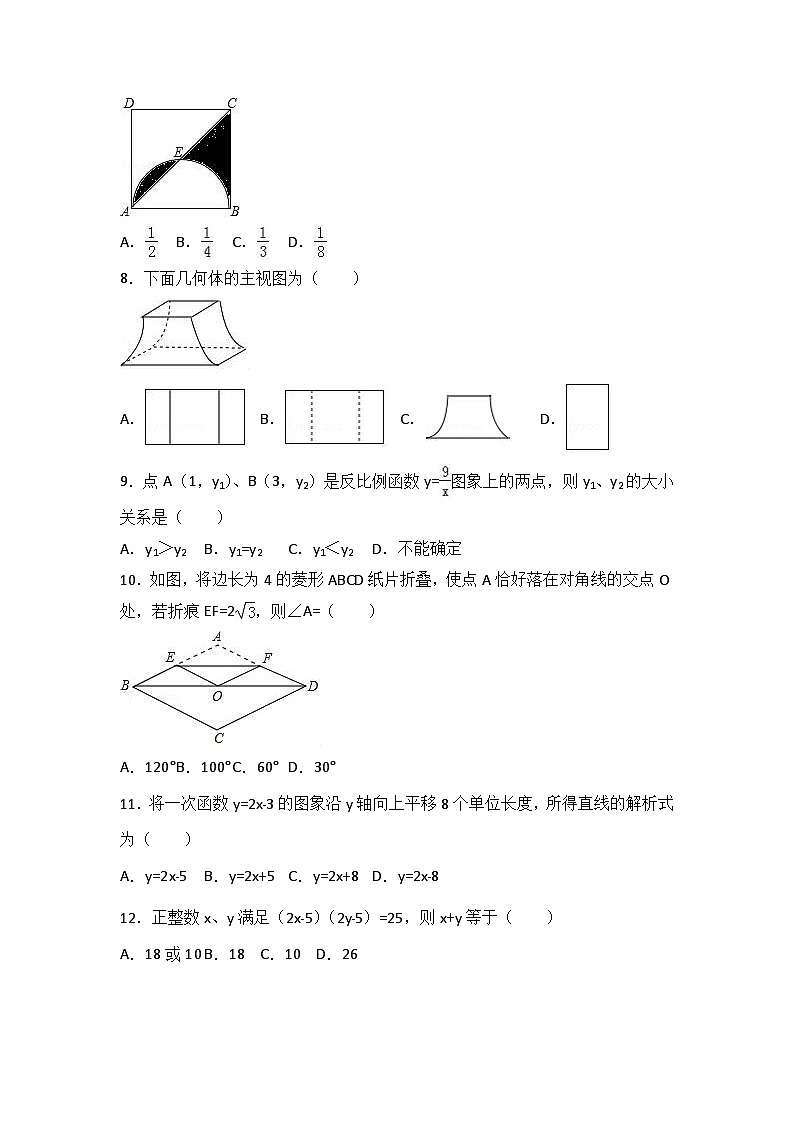
7.小明向如图所示的正方形ABCD区域内投掷飞镖,点E是以AB为直径的半圆与对角线AC的交点.如果小明投掷飞镖一次,则飞镖落在阴影部分的概率为( )
A. B. C. D.
8.下面几何体的主视图为( )
A. B. C. D.
9.点A(1,y1)、B(3,y2)是反比例函数y=图象上的两点,则y1、y2的大小关系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
10.如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2,则∠A=( )
A.120° B.100° C.60° D.30°
11.将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )
A.y=2x﹣5 B.y=2x+5 C.y=2x+8 D.y=2x﹣8
12.正整数x、y满足(2x﹣5)(2y﹣5)=25,则x+y等于( )
A.18或10 B.18 C.10 D.26
二、填空题(请把答案填写在答题卡相应的横线上,每小题3分,共12分)
13.分解因式:xy2+8xy+16x= .
14.如果关于x的方程x2﹣4x+2m=0有两个不相等的实数根,则m的取值范围是 .
15.数据5,6,5,4,10的众数、中位数、平均数的和是 .
16.在平面直角坐标系中,点P(x,y)经过某种变换后得到点P'(﹣y+1,x+2),我们把点P'(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1、P2、P3、P4、…Pn、…,若点P1的坐标为(2,0),则点P2017的坐标为 .
三、解答题(在答题卡上解答,答在本试卷上无效,解答时要写出必要的文字说明、证明过程或演算步骤,共10题,满分102分)
17.(﹣)÷,其中a=2017°+(﹣)﹣1+tan30°.
18.已知平行四边形ABCD.
(1)尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求证:CE=CF.
19.为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型:A喜欢吃苹果的学生;B喜欢吃桔子的学生;C.喜欢吃梨的学生;D.喜欢吃香蕉的学生;E喜欢吃西瓜的学生,并将调查结果绘制成图1和图2 的统计图(不完整).请根据图中提供的数据解答下列问题:
(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的x;
(3)现有5名学生,其中A类型3名,B类型2名,从中任选2名学生参加体能测试,求这两名学生为同一类型的概率(用列表法或树状图法)
20.王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
21.如图,一次函数y=﹣x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=的图象上,求该反比例函数的解析式;
(2)点P(2,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
22.为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
23.如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积(结果保留π和根号).
24.如图1,在△ABC中,设∠A、∠B、∠C的对边分别为a,b,c,过点A作AD⊥BC,垂足为D,会有sin∠C=,则
S△ABC=BC×AD=×BC×ACsin∠C=absin∠C,
即S△ABC=absin∠C
同理S△ABC=bcsin∠A
S△ABC=acsin∠B
通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理:
如图2,在△ABC中,若∠A、∠B、∠C的对边分别为a,b,c,则
a2=b2+c2﹣2bccos∠A
b2=a2+c2﹣2accos∠B
c2=a2+b2﹣2abcos∠C
用上面的三角形面积公式和余弦定理解决问题:
(1)如图3,在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8.求S△DEF和DE2.
解:S△DEF=EF×DFsin∠F= ;
DE2=EF2+DF2﹣2EF×DFcos∠F= .
(2)如图4,在△ABC中,已知AC>BC,∠C=60°,△ABC'、△BCA'、△ACB'分别是以AB、BC、AC为边长的等边三角形,设△ABC、△ABC'、△BCA'、△ACB'的面积分别为S1、S2、S3、S4,求证:S1+S2=S3+S4.
25.△OPA和△OQB分别是以OP、OQ为直角边的等腰直角三角形,点C、D、E分别是OA、OB、AB的中点.
(1)当∠AOB=90°时如图1,连接PE、QE,直接写出EP与EQ的大小关系;
(2)将△OQB绕点O逆时针方向旋转,当∠AOB是锐角时如图2,(1)中的结论是否成立?若成立,请给出证明;若不成立,请加以说明.
(3)仍将△OQB绕点O旋转,当∠AOB为钝角时,延长PC、QD交于点G,使△ABG为等边三角形如图3,求∠AOB的度数.
26.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2?若存在求出点Q的坐标;若不存在请说明理由.
2018年内蒙古赤峰市中考数学试卷
参考答案与试题解析
一、选择题(每小题给出的选项中只有一个符合题意,请将符合题意的选项序号,在答题卡的对应位置上按要求涂黑.每小题3分,共计36分)
1.|(﹣3)﹣5|等于( )
A.﹣8 B.﹣2 C.2 D.8
【考点】1A:有理数的减法;15:绝对值.
【分析】根据分式的减法和绝对值可以解答本题.
【解答】解:|(﹣3)﹣5|
=|﹣3﹣5|
=|﹣8|
=8,
故选D.
2.下列图形中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
【考点】R5:中心对称图形;P3:轴对称图形.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、是轴对称图形,不是中心对称图形,不合题意;
B、不是轴对称图形,是中心对称图形,不合题意;
C、是轴对称图形,也是中心对称图形,符合题意;
D、是轴对称图形,不是中心对称图形,不合题意.
故选:C.
3.风景秀美的赤峰有“草原明珠”的美称,赤峰市全域总面积为90021平方公里.90021用科学记数法表示为( )
A.9.0021×105 B.9.0021×104 C.90.021×103 D.900.21×102
【考点】1I:科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:90021用科学记数法表示为9.0021×104.
故选:B.
4.下列运算正确的是( )
A.3x+2y=5(x+y) B.x+x3=x4 C.x2•x3=x6 D.(x2)3=x6
【考点】47:幂的乘方与积的乘方;35:合并同类项;46:同底数幂的乘法.
【分析】根据合并同类项、同底数幂的乘法、幂的乘方的计算法则计算,对各选项分析判断后利用排除法求解.
【解答】解:A、不是同类项不能合并,故A错误;
B、不是同类项不能合并,故B错误;
C、x2•x3=x5,故C错误;
D、(x2)3=x6,故D正确.
故选:D.
5.直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )
A.65° B.50° C.55° D.60°
【考点】JA:平行线的性质.
【分析】先根据直角为90°,即可得到∠3的度数,再根据平行线的性质,即可得出∠2的度数.
【解答】解:∵Rt△ABC的直角顶点C在直线a上,∠1=35°,
∴∠3=90°﹣35°=55°,
又∵a∥b,
∴∠2=∠3=55°,
故选:C.
6.能使式子+成立的x的取值范围是( )
A.x≥1 B.x≥2 C.1≤x≤2 D.x≤2
【考点】E4:函数自变量的取值范围.
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:根据题意得:,
解得:1≤x≤2.
故选:C.
7.小明向如图所示的正方形ABCD区域内投掷飞镖,点E是以AB为直径的半圆与对角线AC的交点.如果小明投掷飞镖一次,则飞镖落在阴影部分的概率为( )
A. B. C. D.
【考点】X5:几何概率.
【分析】直接利用正方形的性质结合转化思想得出阴影部分面积=S△CEB,进而得出答案.
【解答】解:如图所示:连接BE,
可得,AE=BE,∠AEB=90°,
且阴影部分面积=S△CEB=S△BEC=S正方形ABCD,
故小明投掷飞镖一次,则飞镖落在阴影部分的概率为:.
故选:B.
8.下面几何体的主视图为( )
A. B. C. D.
【考点】U2:简单组合体的三视图.
【分析】根据从正面看得到的图形是主视图,可得答案.
【解答】解:从正面看,
故选:C.
9.点A(1,y1)、B(3,y2)是反比例函数y=图象上的两点,则y1、y2的大小关系是( )
A.y1>y2 B.y1=y2 C.y1<y2 D.不能确定
【考点】G6:反比例函数图象上点的坐标特征.
【分析】根据反比例函数图象的增减性进行填空.
【解答】解:∵反比例函数y=中的9>0,
∴经过第一、三象限,且在每一象限内y随x的增大而减小,
又∵A(1,y1)、B(3,y2)都位于第一象限,且1<3,
∴y1>y2,
故选A.
10.如图,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2,则∠A=( )
A.120° B.100° C.60° D.30°
【考点】PB:翻折变换(折叠问题);L8:菱形的性质.
【分析】连接AC,根据菱形的性质得出AC⊥BD,根据折叠得出EF⊥AC,EF平分AO,得出EF∥BD,得出EF为△ABD的中位线,根据三角形中位线定理求出BD的长,进而可得到BO的长,由勾股定理可求出AO的长,则∠ABO可求出,继而∠BAO的度数也可求出,再由菱形的性质可得∠A=2∠BAO.
【解答】解:
连接AC,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵A沿EF折叠与O重合,
∴EF⊥AC,EF平分AO,
∵AC⊥BD,
∴EF∥BD,
∴E、F分别为AB、AD的中点,
∴EF为△ABD的中位线,
∴EF=BD,
∴BD=2EF=4,
∴BO=2,
∴AO==2,
∴AO=AB,
∴∠ABO=30°,
∴∠BAO=60°,
∴∠BAD=120°.
故选A.
11.将一次函数y=2x﹣3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )
A.y=2x﹣5 B.y=2x+5 C.y=2x+8 D.y=2x﹣8
【考点】F9:一次函数图象与几何变换.
【分析】根据函数图象上加下减,可得答案.
【解答】解:由题意,得
y=2x﹣3+8,
即y=2x+5,
故选:B.
12.正整数x、y满足(2x﹣5)(2y﹣5)=25,则x+y等于( )
A.18或10 B.18 C.10 D.26
【考点】1C:有理数的乘法.
【分析】易得(2x﹣5)、(2y﹣5)均为整数,分类讨论即可求得x、y的值即可解题.
【解答】解:∵xy是正整数,
∴(2x﹣5)、(2y﹣5)均为整数,
∵25=1×25,或25=5×5,
∴存在两种情况:①2x﹣5=1,2y﹣5=25,解得:x=3,y=15,;
②2x﹣5=2y﹣5=5,解得:x=y=5;
∴x+y=18或10,
故选 A.
二、填空题(请把答案填写在答题卡相应的横线上,每小题3分,共12分)
13.分解因式:xy2+8xy+16x= x(y+4)2 .
【考点】55:提公因式法与公式法的综合运用.
【分析】此多项式有公因式,应先提取公因式,再对余下的多项式进行观察,有3项,可采用完全平方公式继续分解.
【解答】解:xy2+8xy+16x
=x(y2+8y+16)
=x(y+4)2.
故答案为:x(y+4)2.
14.如果关于x的方程x2﹣4x+2m=0有两个不相等的实数根,则m的取值范围是 m<2 .
【考点】AA:根的判别式.
【分析】根据方程的系数结合根的判别式,即可得出△=16﹣8m>0,解之即可得出m的取值范围.
【解答】解:∵关于x的方程x2﹣4x+2m=0有两个不相等的实数根,
∴△=(﹣4)2﹣4×2m=16﹣8m>0,
解得:m<2.
故答案为:m<2.
15.数据5,6,5,4,10的众数、中位数、平均数的和是 16 .
【考点】W5:众数;W1:算术平均数;W4:中位数.
【分析】根据众数、中位数和平均数的概念分别求出这组数据的众数、中位数和平均数,再相加即可.
【解答】解:数据5出现了2次,次数最多,所以众数是5;
数据按从小到大排列为4,5,5,6,10,中位数为5;
平均数=(5+6+5+4+10)÷5=6;
5+5+6=16.
故答案为16.
16.在平面直角坐标系中,点P(x,y)经过某种变换后得到点P'(﹣y+1,x+2),我们把点P'(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1、P2、P3、P4、…Pn、…,若点P1的坐标为(2,0),则点P2017的坐标为 (2,0) .
【考点】D2:规律型:点的坐标.
【分析】求得点P2、P3、P4、P5的值,即可发现其中规律,即可解题.
【解答】解:P1 坐标为(2,0),则P2坐标为(1,4),P3坐标为(﹣3,3),P4坐标为(﹣2,﹣1),P5坐标为(2,0),
∴Pn的坐标为(2,0),(1,4),(﹣3,3),(﹣2,﹣1)循环,
∵2017=2016+1=4×504+1,
∴P2017 坐标与P1点重合,
故答案为(2,0).
三、解答题(在答题卡上解答,答在本试卷上无效,解答时要写出必要的文字说明、证明过程或演算步骤,共10题,满分102分)
17.(﹣)÷,其中a=2017°+(﹣)﹣1+tan30°.
【考点】6D:分式的化简求值;6E:零指数幂;6F:负整数指数幂;T5:特殊角的三角函数值.
【分析】先化简分式,然后再化简a的值,从而可求出原式的值.
【解答】解:原式=×﹣×
=﹣
=
由于a=2017°+(﹣)﹣1+tan30°,
∴a=1﹣5+3=﹣1
∴原式=﹣=﹣2
18.已知平行四边形ABCD.
(1)尺规作图:作∠BAD的平分线交直线BC于点E,交DC延长线于点F(要求:尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,求证:CE=CF.
【考点】N2:作图—基本作图;L5:平行四边形的性质.
【分析】(1)作∠BAD的平分线交直线BC于点E,交DC延长线于点F即可;
(2)先根据平行四边形的性质得出AB∥DC,AD∥BC,故∠1=∠2,∠3=∠4.再由AF平分∠BAD得出∠1=∠3,故可得出∠2=∠4,据此可得出结论.
【解答】解:(1)如图所示,AF即为所求;
(2)∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠1=∠2,∠3=∠4.
∵AF平分∠BAD,
∴∠1=∠3,
∴∠2=∠4,
∴CE=CF.
19.为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型:A喜欢吃苹果的学生;B喜欢吃桔子的学生;C.喜欢吃梨的学生;D.喜欢吃香蕉的学生;E喜欢吃西瓜的学生,并将调查结果绘制成图1和图2 的统计图(不完整).请根据图中提供的数据解答下列问题:
(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的x;
(3)现有5名学生,其中A类型3名,B类型2名,从中任选2名学生参加体能测试,求这两名学生为同一类型的概率(用列表法或树状图法)
【考点】X6:列表法与树状图法;VB:扇形统计图;VC:条形统计图.
【分析】(1)根据百分比=计算即可;
(2)求出B、C的人数画出条形图即可;
(3)利用树状图,即可解决问题;
【解答】解:(1)此次抽查的学生人数为16÷40%=40人.
(2)C占40×10%=4人,B占20%,有40×20%=8人,
条形图如图所示,
(3)由树状图可知:两名学生为同一类型的概率为=.
20.王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
【考点】T8:解直角三角形的应用.
【分析】根据题意作出合适的辅助线,可以求得AD和CD的长,进而可以求得DB的长,然后根据勾股定理即可得到AB的长,然后与17比较大小,即可解答本题.
【解答】解:王浩同学能将手机放入卡槽AB内.
理由:作AD⊥BC于点D,
∵∠C=50°,AC=20cm,
∴AD=AC•sin50°=20×0.8=16cm,
CD=AC•cos50°=20×0.6=12cm,
∵BC=18cm,
∴DB=BC﹣CD=18﹣12=6cm,
∴AB==,
∵17=<,
∴王浩同学能将手机放入卡槽AB内.
21.如图,一次函数y=﹣x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=的图象上,求该反比例函数的解析式;
(2)点P(2,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
【考点】GB:反比例函数综合题.
【分析】(1)由直线解析式可求得A、B坐标,在Rt△AOB中,利用三角函数定义可求得∠BAO=30°,且可求得AB的长,从而可求得CA⊥OA,则可求得C点坐标,利用待定系数法可求得反比例函数解析式;
(2)分△PAD∽△ABO和△PAD∽△BAO两种情况,分别利用相似三角形的性质可求得m的值,可求得P点坐标,代入反比例函数解析式进行验证即可.
【解答】解:
(1)在y=﹣x+1中,令y=0可解得x=,令x=0可得y=1,
∴A(,0),B(0,1),
∴tan∠BAO===,
∴∠BAO=30°,
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠CAO=90°,
在Rt△BOA中,由勾股定理可得AB=2,
∴AC=2,
∴C(,2),
∵点C在反比例函数y=的图象上,
∴k=2×=2,
∴反比例函数解析式为y=;
(2)∵P(2,m)在第一象限,
∴AD=OD﹣OA=2﹣=,PD=m,
当△ADP∽△AOB时,则有=,即=,解得m=1,此时P点坐标为(2,1);
当△PDA∽△AOB时,则有=,即=,解得m=3,此时P点坐标为(2,3);
把P(2,3)代入y=可得3≠,
∴P(2,3)不在反比例函数图象上,
把P(2,1)代入反比例函数解析式得1=,
∴P(2,1)在反比例函数图象上;
综上可知P点坐标为(2,1).
22.为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
【考点】B7:分式方程的应用;C9:一元一次不等式的应用.
【分析】(1)设梨树苗的单价为x元,则苹果树苗的单价为(x+2)元,根据两种树苗购买的棵树一样多列出方程求出其解即可;
(2)设购买梨树苗种树苗a棵,苹果树苗则购买棵,根据购买两种树苗的总费用不超过6000元建立不等式求出其解即可.
【解答】解:(1)设梨树苗的单价为x元,则苹果树苗的单价为(x+2)元,
依题意得: =,
解得x=5.
经检验x=5是原方程的解,且符合题意.
答:梨树苗的单价是5元;
(2)设购买梨树苗种树苗a棵,苹果树苗则购买棵,
依题意得:(5+2)+5a≤6000,
解得a≥850.
答:梨树苗至少购买850棵.
23.如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积(结果保留π和根号).
【考点】ME:切线的判定与性质;MO:扇形面积的计算.
【分析】(1)由已知条件得到△BOC是等边三角形,根据等边三角形的性质得到∠1=∠2=60°,由角平分线的性质得到∠1=∠3,根据平行线的性质得到∠OAM=90°,于是得到结论;
(2)根据等边三角形的性质得到∠OAC=60°,根据三角形的内角和得到∠CAD=30°,根据勾股定理得到AD=2,于是得到结论.
【解答】解:(1)∵∠B=60°,
∴△BOC是等边三角形,
∴∠1=∠2=60°,
∵OC平分∠AOB,
∴∠1=∠3,
∴∠2=∠3,
∴OA∥BD,
∴∠BDM=90°,∴∠OAM=90°,
∴AM是⊙O的切线;
(2)∵∠3=60°,OA=OC,
∴△AOC是等边三角形,
∴∠OAC=60°,
∵∠OAM=90°,
∴∠CAD=30°,
∵CD=2,
∴AC=2CD=4,
∴AD=2,
∴S阴影=S梯形OADC﹣S扇形OAC=(4+2)×2﹣=6﹣.
24.如图1,在△ABC中,设∠A、∠B、∠C的对边分别为a,b,c,过点A作AD⊥BC,垂足为D,会有sin∠C=,则
S△ABC=BC×AD=×BC×ACsin∠C=absin∠C,
即S△ABC=absin∠C
同理S△ABC=bcsin∠A
S△ABC=acsin∠B
通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理:
如图2,在△ABC中,若∠A、∠B、∠C的对边分别为a,b,c,则
a2=b2+c2﹣2bccos∠A
b2=a2+c2﹣2accos∠B
c2=a2+b2﹣2abcos∠C
用上面的三角形面积公式和余弦定理解决问题:
(1)如图3,在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8.求S△DEF和DE2.
解:S△DEF=EF×DFsin∠F= 6 ;
DE2=EF2+DF2﹣2EF×DFcos∠F= 49 .
(2)如图4,在△ABC中,已知AC>BC,∠C=60°,△ABC'、△BCA'、△ACB'分别是以AB、BC、AC为边长的等边三角形,设△ABC、△ABC'、△BCA'、△ACB'的面积分别为S1、S2、S3、S4,求证:S1+S2=S3+S4.
【考点】KY:三角形综合题.
【分析】(1)直接利用正弦定理和余弦定理即可得出结论;
(2)方法1、利用正弦定理得出三角形的面积公式,再利用等边三角形的性质即可得出结论;
方法2、先用正弦定理得出S1,S2,S3,S4,最后用余弦定理即可得出结论.
【解答】解:(1)在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8,
∴EF=3,DF=8,
∴S△DEF=EF×DFsin∠F=×3×8×sin60°=6,
DE2=EF2+DF2﹣2EF×DFcos∠F=32+82﹣2×3×8×cos60°=49,
故答案为:6,49;
(2)证明:方法1,∵∠ACB=60°,
∴AB2=AC2+BC2﹣2AC•BCcos60°=AC2+BC2﹣AC•BC,
两边同时乘以sin60°得, AB2sin60°=AC2sin60°+BC2sin60°﹣AC•BCsin60°,
∵△ABC',△BCA',△ACB'是等边三角形,
∴S1=AC•BCsin60°,S2=AB2sin60°,S3=BC2sin60°,S4=AC2sin60°,
∴S2=S4+S3﹣S1,
∴S1+S2=S3+S4,
方法2、令∠A,∠B,∠C的对边分别为a,b,c,
∴S1=absin∠C=absin60°=ab
∵△ABC',△BCA',△ACB'是等边三角形,
∴S2=c•c•sin60°=c2,S3=a•a•sin60°=a2,S4=b•b•sin60°=b2,
∴S1+S2=(ab+c2),S3+S4=(a2+b2),
∵c2=a2+b2﹣2ab•cos∠C=a2+b2﹣2ab•cos60°,
∴a2+b2=c2+ab,
∴S1+S2=S3+S4.
25.△OPA和△OQB分别是以OP、OQ为直角边的等腰直角三角形,点C、D、E分别是OA、OB、AB的中点.
(1)当∠AOB=90°时如图1,连接PE、QE,直接写出EP与EQ的大小关系;
(2)将△OQB绕点O逆时针方向旋转,当∠AOB是锐角时如图2,(1)中的结论是否成立?若成立,请给出证明;若不成立,请加以说明.
(3)仍将△OQB绕点O旋转,当∠AOB为钝角时,延长PC、QD交于点G,使△ABG为等边三角形如图3,求∠AOB的度数.
【考点】RB:几何变换综合题.
【分析】(1)先判断出点P,O,Q在同一条直线上,再判断出△APE≌△BFE,最后用直角三角形的斜边的中线等于斜边的一半即可得出结论;
(2)先判断出CE=DQ,PC=DE,进而判断出△EPC≌△QED即可得出结论;
(3)先判断出CQ,GP分别是OB,OA的垂直平分线,进而得出∠GBO=∠GOB,∠GOA=∠GAO,即可得出结论.
【解答】解:(1)如图1,延长PE,QB交于点F,
∵△APO和△BQO是等腰直角三角形,
∴∠APO=∠BQO=90°,∠AOP=∠BOQ=45°,
∵∠AOB=90°,
∴∠AOP+∠AOB+∠BOQ=180°,
∴点P,O,Q在同一条直线上,
∵∠APO=∠BQO=90°,
∴AP∥BQ,
∴∠PAE=∠FBE,
∵点E是AB中点,
∴AE=BE,
∵∠AEP=∠BEF,
∴△APE≌△BFE,
∴PE=EF,
∴点E是Rt△PQF的斜边PF的中点,
∴EP=EQ;
(2)成立,
证明:∵点C,E分别是OA,AB的中点,
∴CE∥OB,CE=OB,
∴∠DOC=∠ECA,
∵点D是Rt△OQB斜边中点,
∴DQ=OB,
∴CE=DQ,
同理:PC=DE,∠DOC=∠BDE,
∴∠ECA=∠BDE,
∵∠PCE=∠EDQ,
∴△EPC≌△QED,
∴EP=EQ;
(3)如图2,连接GO,∵点D,C分别是OB,OA的中点,△APO与△QBO都是等腰直角三角形,
∴CQ,GP分别是OB,OA的垂直平分线,
∴GB=GO=GA,
∴∠GBO=∠GOB,∠GOA=∠GAO,
设∠GOB=x,∠GOA=y,
∴x+x+y+y+60°=360°
∴x+y=150°,
∴∠AOB=150°.
26.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2?若存在求出点Q的坐标;若不存在请说明理由.
【考点】HF:二次函数综合题.
【分析】(1)可设抛物线解析式为顶点式,由B点坐标可求得抛物线的解析式,则可求得D点坐标,利用待定系数法可求得直线BD解析式;
(2)设出P点坐标,从而可表示出PM的长度,利用二次函数的性质可求得其最大值;
(3)过Q作QG∥y轴,交BD于点G,过Q和QH⊥BD于H,可设出Q点坐标,表示出QG的长度,由条件可证得△DHG为等腰直角三角形,则可得到关于Q点坐标的方程,可求得Q点坐标.
【解答】解:
(1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵点B(3,0)在该抛物线的图象上,
∴0=a(3﹣1)2+4,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3,
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD解析式为y=kx+3,
把B点坐标代入可得3k+3=0,解得k=﹣1,
∴直线BD解析式为y=﹣x+3;
(2)设P点横坐标为m(m>0),则P(m,﹣m+3),M(m,﹣m2+2m+3),
∴PM=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣)2+,
∴当m=时,PM有最大值;
(3)如图,过Q作QG∥y轴交BD于点G,交x轴于点E,作QH⊥BD于H,
设Q(x,﹣x2+2x+3),则G(x,﹣x+3),
∴QG=|﹣x2+2x+3﹣(﹣x+3)|=|﹣x2+3x|,
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°,
当△BDQ中BD边上的高为2时,即QH=HG=2,
∴QG=×2=4,
∴|﹣x2+3x|=4,
当﹣x2+3x=4时,△=9﹣16<0,方程无实数根,
当﹣x2+3x=﹣4时,解得x=﹣1或x=4,
∴Q(﹣1,0)或(4,﹣5),
综上可知存在满足条件的点Q,其坐标为(﹣1,0)或(4,﹣5).
2023年内蒙古赤峰市中考数学试卷: 这是一份2023年内蒙古赤峰市中考数学试卷,共36页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018年内蒙古赤峰市中考数学真题及答案: 这是一份2018年内蒙古赤峰市中考数学真题及答案,共28页。试卷主要包含了选择题,填空题,简答题等内容,欢迎下载使用。
2023年内蒙古赤峰市中考数学试卷(含解析): 这是一份2023年内蒙古赤峰市中考数学试卷(含解析),共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












