安徽省合肥市2021-2022两年小升初数学真题知识点分类汇编-10立体图形

安徽省合肥市2021-2022两年小升初数学真题知识点分类汇编-10立体图形

一、选择题

1．（2022·安徽合肥·统考小升初真题）媛媛用棱长1厘米的正方体小木块摆了一个几何体，从前面、右面和上面观察这个几何体，看到的图形如图，媛媛摆这个几何体用了（    ）个小木块。

A．5 B．6 C．7

2．（2022·安徽合肥·统考小升初真题）两个圆锥的底面积相等，第一个圆锥与第二个圆锥的高之比是5∶7，第一个圆锥的体积是35立方厘米，第二个圆锥的体积是（    ）立方厘米。

A．25 B．49 C．84

3．（2022·安徽合肥·统考小升初真题）下面图形都是由相同的小正方体搭成的。选择（    ）能搭成左面的模型。

A．①② B．①④ C．②④

4．（2022·安徽合肥·统考小升初真题）用硬纸板做正方体盒子，正方体展开图的6个面上分别画着1、2、3、4、5、6个圆点。下面（     ）图可以围成有一组相对面的点数的和是10的正方体。

A． B． C．

5．（2021·安徽合肥·统考小升初真题）下面三幅图中，不可能是圆柱侧面展开图的是（    ）。

A． B． C．

6．（2021·安徽合肥·统考小升初真题）一个近似长方体的物体，它的长15厘米、宽7厘米、高0.6厘米。这个物体一定是（    ）。

A．一张银行卡 B．一部手机 C．一本新华字典

7．（2021·安徽合肥·统考小升初真题）一个圆柱和一个圆锥等底等高，它们的体积之差是36立方厘米，圆柱的体积是（    ）立方厘米。

A．54 B．18 C．108 D．27

二、解答题

8．（2022·安徽合肥·统考小升初真题）古代的铜钱都是“外圆内方”，铜钱内正方形的边长是0.5厘米。小明把20枚相同的古代铜钱叠在一起的形状如图，每枚铜钱的体积是多少立方厘米？（取值3.14）

9．（2022·安徽合肥·统考小升初真题）如图，妈妈要把两个半径是8厘米、高30厘米的圆柱形花瓶放入一个长方体包装盒里。

（1）每个花瓶的容积是多少毫升？（花瓶的厚度不计）

（2）接头处不计，做这个包装盒（有盖）至少需要硬纸板多少平方厘米？

10．（2021·安徽合肥·统考小升初真题）一个健康的成年人每天大约需要喝2000毫升的水才能满足身体的正常需要。刘红的水杯是一个内直径8厘米，内高是10厘米的圆柱形，刘红每天大约需要用这个杯子喝多少杯水？（得数保留整数）

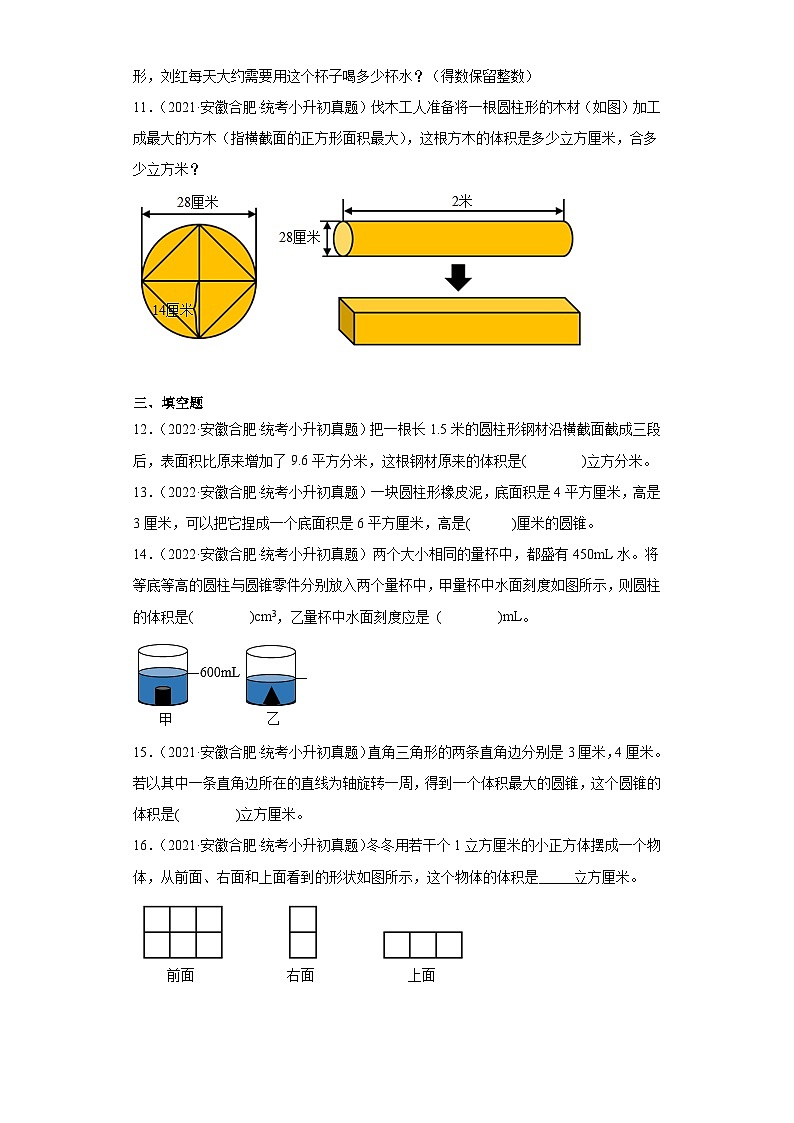
11．（2021·安徽合肥·统考小升初真题）伐木工人准备将一根圆柱形的木材（如图）加工成最大的方木（指横截面的正方形面积最大），这根方木的体积是多少立方厘米，合多少立方米？

三、填空题

12．（2022·安徽合肥·统考小升初真题）把一根长1.5米的圆柱形钢材沿横截面截成三段后，表面积比原来增加了9.6平方分米，这根钢材原来的体积是(        )立方分米。

13．（2022·安徽合肥·统考小升初真题）一块圆柱形橡皮泥，底面积是4平方厘米，高是3厘米，可以把它捏成一个底面积是6平方厘米，高是(      )厘米的圆锥。

14．（2022·安徽合肥·统考小升初真题）两个大小相同的量杯中，都盛有450mL水。将等底等高的圆柱与圆锥零件分别放入两个量杯中，甲量杯中水面刻度如图所示，则圆柱的体积是(        )cm3，乙量杯中水面刻度应是 (        )mL。

15．（2021·安徽合肥·统考小升初真题）直角三角形的两条直角边分别是3厘米，4厘米。若以其中一条直角边所在的直线为轴旋转一周，得到一个体积最大的圆锥，这个圆锥的体积是(        )立方厘米。

16．（2021·安徽合肥·统考小升初真题）冬冬用若干个1立方厘米的小正方体摆成一个物体，从前面、右面和上面看到的形状如图所示，这个物体的体积是_____立方厘米。

参考答案：

1．A

【分析】根据上面观察的图形可知，一共有2层，下层有2个小正方体，上层有1个小正方体，再根据右面和上面看到的图形上层有2个小正方体；看到的图形为：，共有3＋2＝5个小正方体组成，据此解答。

【详解】根据分析可知，共用3＋2＝5（个）

故答案为：A

【点睛】本题考查根据三视图确定物体，利用三视图确定小正方形的个数，进行解答。

2．B

【分析】圆锥的体积＝Sh。两个圆锥的底面积相等，第一个圆锥与第二个圆锥的高之比是5∶7，则第一个圆锥与第二个圆锥的体积之比是5∶7，第二个圆锥的体积是第一个圆锥体积的。已知第一个圆锥的体积是35立方厘米，用35乘即可求出第二个圆锥的体积。

【详解】35×＝49（立方厘米）

故答案为：B

【点睛】本题考查了圆锥的体积和比的综合应用。根据圆锥的体积公式，得出“第一个圆锥与第二个圆锥的体积之比是5∶7”是解题的关键。

3．B

【分析】观察图形可知，这个几何体是由长2个、宽是2个、高是3个小正方体拼成；共有2×2×3＝12个小正方体组成；由此逐项分析选项进行解答。

【详解】A．①和②；①是由9个小正方体搭成，②是5个小正方体搭成，9＋5＝14（个）；①和②不能搭成；

B．①和④；①是9个小正方体搭成，④是3个小正方体搭成，9＋2＝12（个）；①和④能搭成。

C．②和④；②是5个小正方体搭成，④是3个小正方体搭成，5＋3＝8（个）；②和④不能搭成；

故答案为：B

【点睛】本题考查从不同方向观察物体和几何图，以及长方体的体积公式的应用。

4．C

【详解】三个图形都属于正方体展开图的“1—4—1”型，折成正方体，第一行的正方形与第三行的正方形相对，第二行的第一个正方形与第三个正方形相对，第二个正方形与第四个正方形相对，据此即可确定围成有一组相对面的点数和是10的正方体的硬纸板是哪个图形。

【解答】解：A.围成正方体后，三组对面的和分别是8、6、7；

B.围成正方体后，三组对面的和分别是7、7、7；

C.围成正方体后，三组对面的和分别是7、4、10。

故选：C。

【点评】正方体展开图分四种类型，11种情况，每种情况折成正方体后哪些面相对是有规律的，可自己动手操作一下并记住规律，能快速解答此类题。

5．C

【分析】根据圆柱侧面展开图的特征，圆柱的侧面沿高展开是一个长方形，如果不沿高线剪，斜着剪开将会得到一个平行四边形，如果侧面不是规则来剪开的可以得到选项B的图形。据此解答。

【详解】根据圆柱侧面展开图的特征可知：圆柱的侧面展开图可能是长方形、也可能是平行四边形、或是不规则图形，但是不可能是梯形。

故答案为：C。

【点睛】本题考查了圆柱的侧面展开图，同一个立体图形按不同的方式展开，得到的平面展开图是不一样的，熟记常见几何体的侧面展开图。圆柱的侧面展开图不仅可以是平行四边形，而且还可以是其它图形，这要取决于侧面展开时是如何剪开的。

6．B

【分析】长15厘米、宽7厘米，大约是手机的尺寸。高0.6厘米，也是手机的厚度，据此判断。

【详解】一个近似长方体的物体，它的长15厘米、宽7厘米、高0.6厘米。这个物体一定是一部手机。

故答案为：B。

【点睛】此题主要考查了长方体的特征，要熟练掌握。

7．A

【分析】等底等高的圆柱的体积是圆锥体积的3倍，设圆锥的体积为x立方厘米，则圆柱的体积为3x立方厘米，圆柱的体积与圆锥体积之差是36立方厘米，列方程：3x－x＝36，解方程，求出圆锥的体积，进而求出圆柱的体积。

【详解】解：设圆锥的体积为x立方厘米，则圆柱的体积为3x立方厘米

3x－x＝36

2x＝36

x＝36÷2

x＝18（立方厘米）

圆柱体积：3×18＝54（立方厘米）

故答案为：A

【点睛】本题考查等底等高的圆柱体积和圆锥体积的关系，根据它们的关系，列方程，解方程。

8．0.578立方厘米

【分析】根据图示可知，20枚相同的古代铜钱叠在一起的体积等于圆柱的体积减去长方体的体积。利用圆柱的体积公式：V＝πr2h，长方体体积公式：V＝abh，计算出20枚铜钱的体积，再除以20即可求出每枚铜钱的体积。

【详解】3.14×（2÷2）2×4－0.5×0.5×4

＝12.56－1

＝11.56（立方厘米）

11.56÷20＝0.578（立方厘米）

答：每枚铜钱的体积是0.578立方厘米。

【点睛】本题主要考查组合图形的体积，关键利用圆柱、长方体的体积公式计算。

9．（1）6028.8毫升（2）3904平方厘米

【分析】（1）圆柱的容积＝底面积×高＝πr2h，据此代入数据计算；

（2）根据题意，这个长方体包装盒的长是8×2×2＝32（厘米），宽是8×2＝16（厘米）。高是30厘米。长方体的表面积＝（长×宽＋长×高＋宽×高）×2，据此求出做这个包装盒（有盖）至少需要硬纸板多少平方厘米。

【详解】（1）3.14×82×30

＝3.14×64×30

＝6028.8（立方厘米）

＝6028.8毫升

答：每个花瓶的容积是6028.8毫升。

（2）长：8×2×2＝32（厘米）

宽：8×2＝16（厘米）

（32×16＋32×30＋16×30）×2

＝（512＋960＋480）×2

＝1952×2

＝3904（平方厘米）

答：做这个包装盒（有盖）至少需要硬纸板3904平方厘米。

【点睛】本题考查圆柱的容积和长方体的表面积的应用。熟练运用圆柱的容积和长方体的表面积公式是解题的关键。

10．4杯

【分析】根据圆柱的容积（体积）公式：V＝πr2h，把数据代入公式求出这个水杯的容积，然后根据“包含”除法的意义，用除法解答。

【详解】2000毫升＝2000立方厘米

2000÷[3.14×（8÷2）2×10]

＝2000÷[3.14×16×10]

＝2000÷502.4

≈4（杯）

答：刘红每天大约需要用这个杯子喝4杯。

【点睛】此题主要考查圆柱的容积（体积）公式在实际生活中的应用，关键是熟记公式，注意：容积单位与体积单位之间的换算。

11．78400立方厘米，合0.0784立方米

【分析】根据题意，把圆柱形木材加工成最大的方木，方木底面正方形的对角线等于圆的直径，把这个正方形看作完全相同的两个三角形，每个三角形的底等于直径，高等于半径，根据三角形的面积公式：S＝ah÷2，求出方木的底面积，然后根据长方体的体积公式：V＝Sh，把数据代入公式解答。

【详解】2米＝200厘米

28×（28÷2）÷2×2×200

＝28×14÷2×2×200

＝392÷2×2×200

＝392×200

＝78400（立方厘米）

78400立方厘米＝0.0784立方米

答：这根方木的体积是78400立方厘米，合0.0784立方米。

【点睛】此题主要考查长方体的体积公式的灵活运用，关键是明白：方木底面正方形的对角线等于圆的直径，把这个正方形看作完全相同的两个三角形。

12．36

【分析】圆柱形钢材沿横截面截成三段后，表面积比原来增加了4个横截面面积。已知表面积比原来增加了9.6平方分米，用9.6除以4即可求出圆柱的横截面面积。圆柱的体积＝底面积×高，用这根钢材的横截面面积乘长即是钢材的体积。

【详解】1.5米＝15分米

9.6÷4×15

＝2.4×15

＝36（立方分米）

【点睛】本题考查立体图形的切拼和圆柱体积的应用。明确圆柱表面积比原来增加了4个横截面面积，继而求出横截面的面积是解题的关键。

13．6

【分析】根据题干，利用圆柱的体积公式V＝Sh可以求得这个圆柱形橡皮泥的体积，也就是捏成后的圆锥的体积，然后利用圆锥的高＝圆锥的体积×3÷圆锥的底面积即可。

【详解】4×3×3÷6

＝12×3÷6

＝36÷6

＝6（厘米）

【点睛】此题主要考查了圆柱与圆锥体积公式的灵活应用，抓住前后的体积大小不变，是解决此类问题的关键。

14．     150     500

【分析】用甲量杯现在刻度－原来水的体积＝圆柱体积；用圆柱体积÷3＝圆锥体积，圆锥体积＋原来水的体积＝乙量杯现在水面刻度。

【详解】600－450＝150（mL）

150÷3＋450

＝50＋450

＝500（mL）

【点睛】等底等高的圆柱和圆锥，圆柱体积是圆锥的3倍。

15．50.24

【分析】根据题意，如果以3厘米长的直角边为轴旋转一周，得到一个底面半径是4厘米，高3厘米的圆锥；如果以4厘米长的直角边为轴旋转一周，得到一个底面半径是3厘米，高4厘米的圆锥；根据圆锥的体积公式：V＝πr2h，把数据代入公式求出两个圆锥的体积进行比较即可。

【详解】×3.14×42×3

＝×3.14×16×3

＝50.24（立方厘米）

×3.14×32×4

＝×3.14×9×4

＝37.68（立方厘米）

50.24＞37.68

即这个圆锥的体积最大是50.24立方厘米。

【点睛】此题主要考查圆锥体积公式的灵活运用，关键是熟记公式。

16．6

【分析】从前面看的图形可知，此物体有两层三列，每一层的三列上均有小正方体，从右面看到图形可知，此物体只有一行，由此可画出立体图形，计算有几个小正方体，便可得到答案。

【详解】物体的立体图形如图：

共有2×3＝6（个）小正方体。

它的体积为6×1×1×1＝6（cm3）。

【点睛】本题主要考查了从不同方向观察物体和几何体，需要学生具备较好的空间观念。