2023年高考数学押题卷02（甲卷文科）（含考试版、参考答案、全解全析、答题卡）

这是一份2023年高考数学押题卷02（甲卷文科）（含考试版、参考答案、全解全析、答题卡），文件包含2023年高考数学押题卷02全国甲卷文科全解全析A4docx、2023年高考数学押题卷02全国甲卷文科参考答案A4docx、2023年高考数学押题卷02全国甲卷文科考试版A4docx、2023年高考数学押题卷02全国甲卷文科考试版A3docx、2023年高考数学押题卷02全国甲卷文科答题卡docx等5份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。
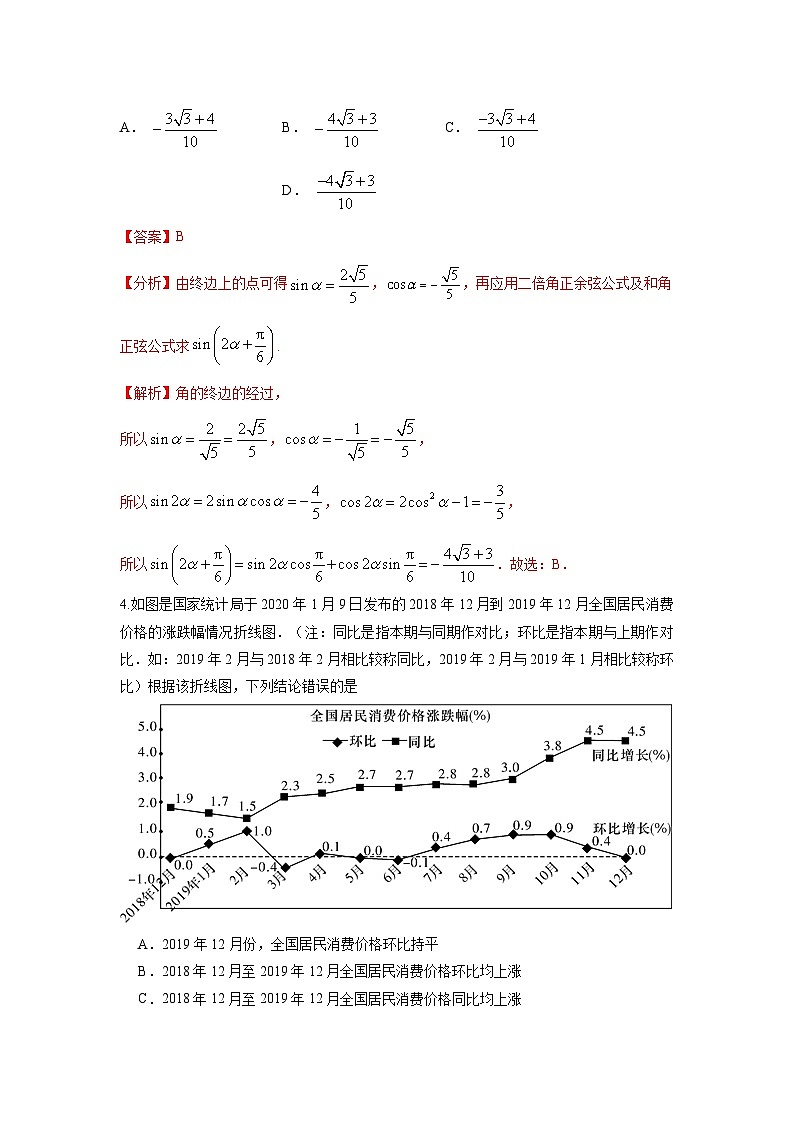
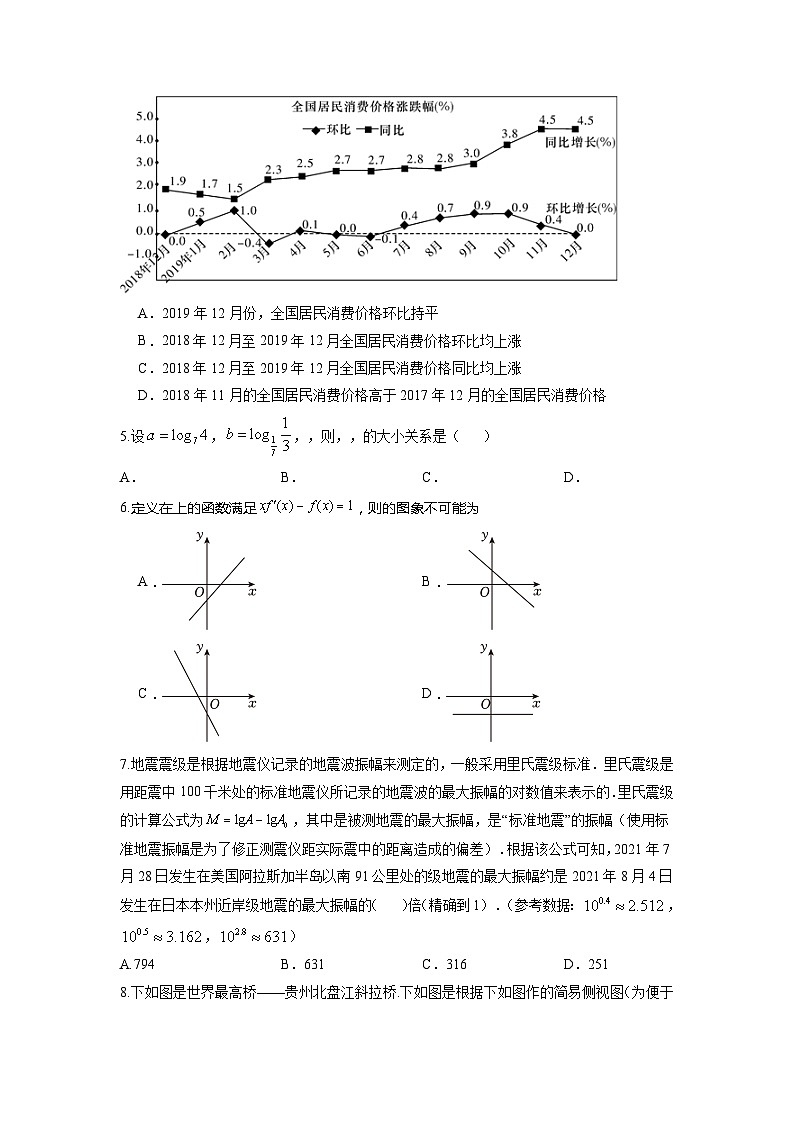
2023年高考押题预测卷02【全国甲卷】数  学（文科）参考答案123456789101112CDBBCBADCBDD1.C 【解析】：，所以，，或．故选：．2. D【解析】解：，在复平面对应的点为，所以在复平面对应的点在第四象限.故选：D.3. B 【解析】角的终边的经过，所以，，所以，，所以．故选：B．4.B【解析】：对于选项，从同比来看，同比均为正数，即同比均上涨，故正确，对于选项，从环比来看，2018年12月至2019年12月全国居民消费价格环比图象有升有降，即环比有涨有跌，故错误，对于选项，从环比同比来看，2018年12月至2019年12月全国居民消费价格同比均上涨，故正确，对于选项，设2018年12月，2018年11月，2017年12月的全国居民消费价格分别为，，，由题意可得，，则，故正确，故选：．C 【解析】因为在上为增函数，所以，即．因为在上为增函数，所以，即，所以．故选：C．6.B【解析】：当时，由可得，排除选项；当时，可得，则，所以为常数），所以，选项满足，选项满足，选项满足．故选：．7. A 【解析】由题意，即，则；当时，地震的最大振幅，当时，地震的最大振幅，所以，即；故选：A．8.D 【解析】因为，所以，因为，所以∽，所以，所以，因为，，所以，设，分别为的中点，因为，所以，所以为的中点，因为，，所以，所以，所以，所以；故选：D9.C 【解析】由图可知，,则最小正周期，，，把点  代入, 可得 , 即，, 又，，故.将图象上所有点的横坐标缩小到原来的倍（纵坐标不变），可得，再将图象向右平移个单位长度得，即，故  的最小正周期是, 故 A错误; 令, 求得 ,不是的最大或最小值, 故的图象不关于直线对称, 故B错误;在区间上, ,令，函数是增函数,故在区间上单调递增，故C正确；在区间上, ，此时当时，取最小值，最小值为，故D错误；故选: C.B【解析】依题意作上图，∵P-ABCD是正四棱锥，∴底面ABCD是正方形，并且点P在底面的投影为正方形ABCD的中心， 即平面ABCD，外接球的球心必定在上，设球心为O，由题意 ，则,连接BO，则BO为外接球的半径R， ，并且PO=R，∴在 中， ， ，解得R=5，外接球的表面积 ，故选：B.D  【解析】：，△，，，且，，，，，，，，，即离心率，，渐近线的斜率为，为等腰三角表，的面积为．综上所述：错误，正确．故选：．D 解析】解：令，即，则，令，即，则，因为定义域为，所以是奇函数，由，用替代，得，因为是奇函数，所以，，且，则，因为当时，，所以，，即，所以在上递增，又是定义域为的奇函数，所以在上递增，则等价于，解得，故选：D　．              14.  或    15. ##0.375            16. ##13. 【解析】作出不等式组表示的平面区域，如图中阴影（含边界），其中，目标函数，即表示斜率为，纵截距为的平行直线系，画直线，平移直线到直线，当直线过点时，直线的纵截距最大，最大，所以的最大值.故答案为： 14.或 【解析】解：将圆方程化为圆的标准方程，得圆心，半径为，当过点的直线斜率不存在时，直线方程为是圆的切线，满足题意；当过点的直线斜率存在时，可设直线方程为，即，利用圆心到直线的距离等于半径得，解得，即此直线方程为，故答案为：或 ．##0.375【解析】设圆锥的底面圆半径为，母线为，依题意，，即有，高，如图，设圆柱的底面圆半径为，母线为，则有，由得：，又，即，于是，所以圆柱PO的体积与圆锥SO的体积的比为.故答案为： 【点睛】关键点睛：涉及与旋转体有关的组合体，利用轴截面，借助平面几何知识解题是解决问题的关键. 16. ## 【解析】方法一：设椭圆的半焦距为，左焦点为，则因为两点关于原点对称，所以，又，所以，所以四边形为矩形，设，因为，所以，由椭圆的定义可得，，在，，，，所以，所以，故，，在中，，所以，所以，所以离心率.故答案为：.方法二：设椭圆的半焦距为，点的坐标为，点的坐标为，则点的坐标为，点的坐标为，且①，②，②×4-①可得，，因为经过右焦点，，所以，所以，故，所以，又，所以，因为，所以，又，所以，所以，所以，即，又，所以，所以离心率.故答案为：.17.【答案】（1），年水产品年产量能实现目标    （2）有的把握认为“渔业科技推广人员配比和年产量”有关系【解析】【分析】（1）利用最小二乘法即可求得线性回归方程，代入得到预估值，由可得结论；（2）由已知数据可得列联表，进而求得，对比临界值表可得结论.【解析】（1）由表格数据知：，，，，，，关于的线性回归方程为：，当时，，年水产品年产量能实现目标.（2）列联表如下： 渔业年产量超过万吨的地区渔业年产量不超过万吨的地区合计有渔业科技推广人员高配比的地区   没有渔业科技推广人员高配比的地区   合计   则，有的把握认为“渔业科技推广人员配比和年产量”有关系.18.【答案】（1），    （2）答案见解析【解析】（1）设等差数列的公差为，依题意可得，则解得，，所以，数列的通项公式为.综上：  （2）选① 由（1）可知：  ∴∵∴选②由（1）可知：∴∵选③由（1）可知：，∴∵则于是得两式相减得，所以.【答案】（1）证明见解析    （2）证明见解析，2【解析】（1）记，在中，，，在中，，由余弦定理得，所以，所以AC⊥BC，因为平面ACD⊥平面ABC，平面平面ABC=AC，BC平面ABC，所以BC⊥平面ACD，又平面ACD，所以；（2）由题意，，因为P为BD的中点，，所以，即.20.【答案】（1）    （2）存在，理由见解析【解析】【分析】（1）由焦半径公式求出，求出抛物线方程；（2）设出直线方程，与抛物线方程联立得到点坐标，同理得到点坐标，利用得到，求出，求出定点坐标.【解析】（1）由抛物线的定义得，解得，则抛物线的标准方程为.（2）依题意知直线与直线的斜率存在，设直线方程为，由得直线方程为：，由，解得，由，解得由得，假定在轴上存在点使得，设点，则由（1）得直线斜率，直线斜率，由得，则有，即，整理得，显然当时，对任意不为0的实数，恒成立，即当时，恒成立，恒成立，所以轴上存在点使得.【点睛】处理定点问题的思路：（1）确定题目中的核心变量（此处设为），（2）利用条件找到与过定点的曲线的联系，得到有关与的等式，（3）所谓定点，是指存在一个特殊的点，使得无论的值如何变化，等式恒成立，此时要将关于与的等式进行变形，直至找到，①若等式的形式为整式，则考虑将含的式子归为一组，变形为“”的形式，让括号中式子等于0，求出定点；②若等式的形式是分式，一方面可考虑让分子等于0，一方面考虑分子和分母为倍数关系，可消去变为常数.21.【答案】（1）在上单调递增，上单调递减；极大值，无极小值    （2）证明见解析【解析】【分析】（1）求出函数的导数, 解关于导函数的不等式，求出函数的单调区间即可;（2）通过讨论的范围，求出函数的单调区间, 求出函数的最小值, 结合函数的零点个数求出的范围即可.【解析】（1）当时，，由得，，由得，或∴在上单调递增，上单调递减，∴在处取得极大值，无极小值.（2）∵，∴由，得，或①当时，，在上单调递增∵，∴，故在上有唯一零点②当时，得或∴在上单调递增，在上单调递减，在上单调递增∵，∴，故在上有唯一零点综上：当时，只有一个零点.22．【答案】（1）；    （2）【解析】【分析】（1）把曲线C的方程两边平方相加可求曲线C的普通方程,利用两角和的余弦公式可求直线l的直角坐标方程;（2）设，由题意可得，计算可求点P横坐标的取值范围.【解析】（1）由曲线的参数方程为（为参数），可得由,得,即,曲线的普通方程为,直线的直角坐标方程为（2）设,连接，易得，若,则，在中，，,,两边平方得,解得,点横坐标的取值范围为23．【答案】（1）；    （2）证明见解析.【分析】（1）根据给定条件，分段解含绝对值符号的不等式作答.（2）利用（1）中信息，借助函数单调性求出c，再利用作差法结合均值不等式推理作答.【解析】（1）依题意，，于是不等式化为：或或，解得，所以不等式的解集.（2）由（1）可知：函数在上单调递增，在上单调递减，，即，由得，即，于是，当且仅当，即时取等号，所以.