数学冀教版九年级下第三十章测试题

这是一份数学冀教版九年级下第三十章测试题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
 第三十章 二次函数 一、选择题 1.将y=x2向上平移2个单位后所得到的抛物线的解析式为（   ）            A. y=x2﹣2                        B. y=x2+2                        C. y=（x﹣2）2                        D. y=（x+2）22.将二次函数y=x2的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是（     ）            A. y=（x-1）2+2               B. y=（x+1）2+2               C. y=（x-1）2-2               D. y=（x+1）2-23.如图，抛物线y=ax2+bx+c与x轴交于点（-1，0），对称轴为x=1，则下列结论中正确的是（　　）
  A. a＞0                                 B. 当x＞1时，y随x的增大而增大
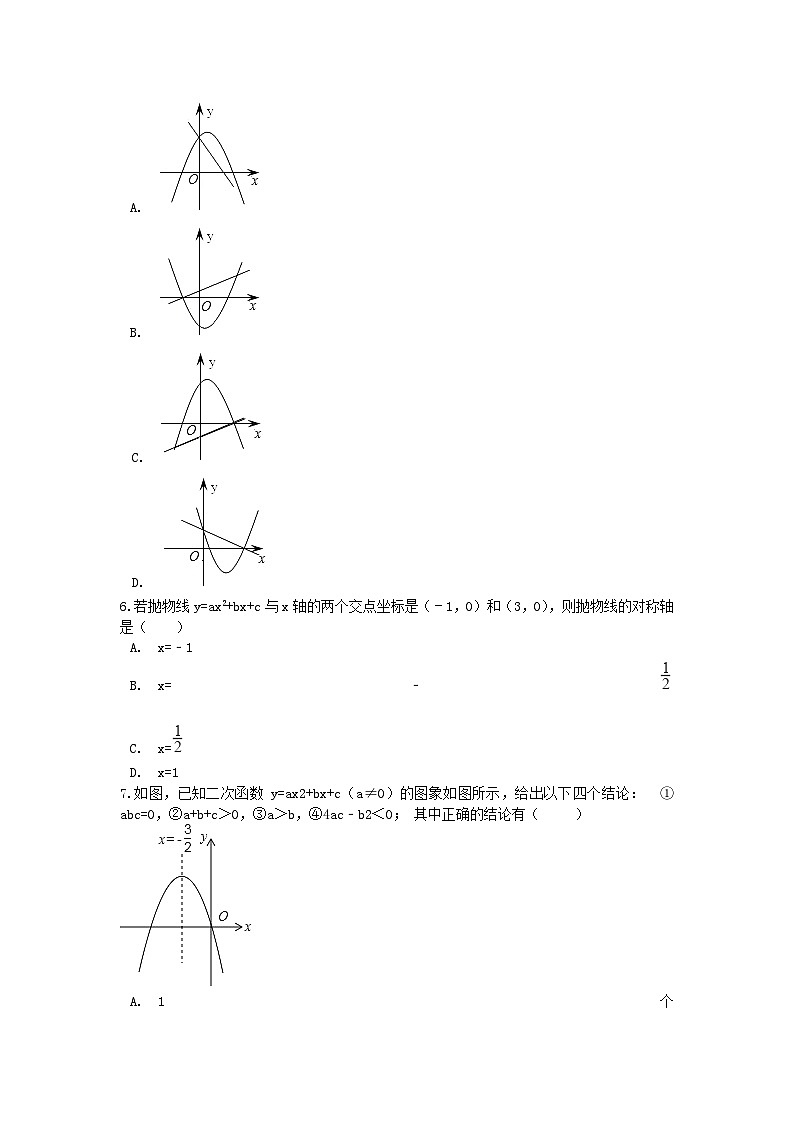
C. c＜0                             D. x=3是一元二次方程ax2+bx+c=0的一个根4.将抛物线y=x2﹣4x﹣3向左平移3个单位，再向上平移5个单位，得到抛物线的表达式为（   ）            A. y=（x+1）2﹣2          B. y=（x﹣5）2﹣2            C. y=（x﹣5）2﹣12          D. y=（x+1）2﹣125.二次函数y=ax2+bx+c与一次函数y=ax+c，它们在同一直角坐标系中的图象大致是（  ）            A.            B.            C.            D. 6.若抛物线y=ax2+bx+c与x轴的两个交点坐标是（﹣1，0）和（3，0），则抛物线的对称轴是（　　）            A. x=﹣1                                  B. x=﹣                                  C. x=                                  D. x=17.如图，已知二次函数 y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论：  ①abc=0，②a+b+c＞0，③a＞b，④4ac﹣b2＜0； 其中正确的结论有（   ）
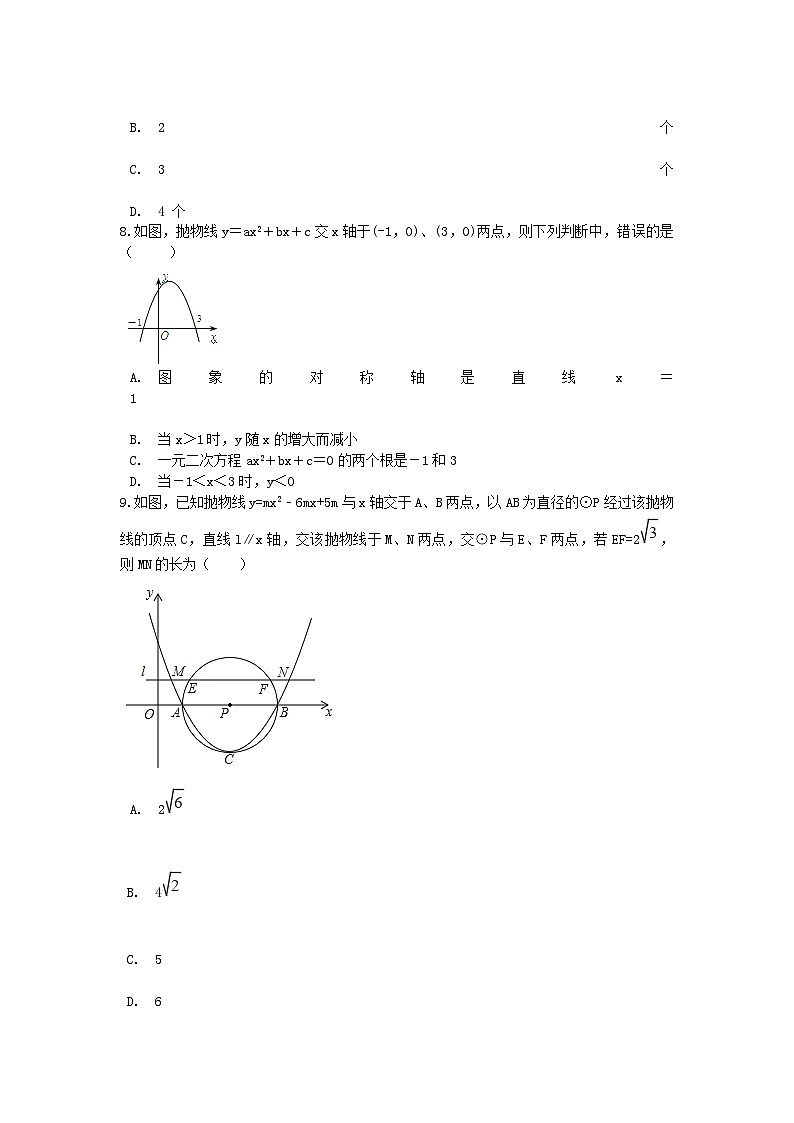
 A. 1 个                                    B. 2 个                                     C. 3 个                                     D. 4 个8.如图，抛物线y＝ax2＋bx＋c交x轴于(-1，0)、(3，0)两点，则下列判断中，错误的是（   ）
 A. 图象的对称轴是直线x＝1                                        B. 当x＞1时，y随x的增大而减小
C. 一元二次方程ax2＋bx＋c＝0的两个根是－1和3     D. 当－1＜x＜3时，y＜09.如图，已知抛物线y=mx2﹣6mx+5m与x轴交于A、B两点，以AB为直径的⊙P经过该抛物线的顶点C，直线l∥x轴，交该抛物线于M、N两点，交⊙P与E、F两点，若EF=2， 则MN的长为（　　）
 A. 2                                        B. 4                                        C. 5                                        D. 610.抛物线y＝a（x＋1）（x－3）（a≠0）的对称轴是直线（   ）            A. x＝1                                  B. x＝－1                                  C. x＝－3                                  D. x＝311.已知二次函数y=a（x﹣1）2+b有最小值﹣1，则a，b的大小关系为（     ）            A. a＜b                                B. a=b                                C. a＞b                                D. 大小不能确定12.某商店经营皮鞋，所获利润y(元)与销售单价x(元)之间的关系为y=－x2+24x+2956，则获利最多为(     )．            A. 3144                                    B. 3100                                    C. 144                                    D. 295613.如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a+b=0；
②abc＞0；
③方程ax2+bx+c=3有两个相等的实数根；
④抛物线与x轴的另一个交点是（﹣1，0）；
⑤当1＜x＜4时，有y2＜y1  ，
其中正确的是（   ）
 A. ①②③                                B. ①③④                                C. ①③⑤                                D. ②④⑤二、填空题 14.抛物线y=（x﹣2）2+1的顶点坐标是________．    15.二次函数y=x2+4x﹣3中，当x=﹣1时，y的值是________．    16.将抛物线y=﹣x2先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为________．    17.如图，正方形的边长为4，以正方形中心为原点建立平面直角坐标系，作出函数y= x2与y=﹣ x2的图象，则阴影部分的面积是________．  18.某工厂计划为一批长方体形状的产品涂上油漆，长方体的长和宽相等，高比长多0.5m，若长方体的长和宽用x（m）表示，长方体需涂油漆的表面积S（m2）表示为________．    19.若A（x1  ， y1）、B（x2  ， y2）是一次函数y=﹣（x+1）2﹣2图象上不同的两点，且x1＞x2＞﹣1，记m=（x1﹣x2）（ y1﹣y2），则m________0．（填“＞”或“＜”）    20.如图所示，二次函数y=ax2+bx+c（a≠0）的图象，有下列4个结论：①abc＞0；②b＞a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的是________  21.二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②b2=4ac；③4a+2b+c＞0；④3a+c＞0，其中正确的结论是________．（写出正确命题的序号）  三、解答题 22.已知二次函数y=x2+2x+m的图象过点A（3，0）．
（1）求m的值；
（2）当x取何值时，函数值y随x的增大而增大．         如图，已知正方形OABC的边长为2，顶点A，C分别在x轴，y轴的正半轴上，E点是BC的中点，F是AB延长线上一点且FB=1．
（1）求经过点O、A、E三点的抛物线解析式；
（2）点P在抛物线上运动，当点P运动到什么位置时△OAP的面积为2，请求出点P的坐标；
（3）在抛物线上是否存在一点Q，使△AFQ是等腰直角三角形？若存在直接写出点Q的坐标；若不存在，请说明理由．
      24.如图，抛物线y= x2﹣x+a与x轴交于点A，B，与y轴交于点C，其顶点在直线y=﹣2x上．
 （1）求a的值；    （2）求A，B的坐标；    （3）以AC，CB为一组邻边作▱ACBD，则点D关于x轴的对称点D′是否在该抛物线上？请说明理由．        25.如图①，若二次函数y= x2+bx+c的图象与x轴交于A（﹣2，0），B（3，0）两点，点A关于正比例函数y= x的图象的对称点为C．
 （1）求b、c的值；    （2）证明：点C在所求的二次函数的图象上；    （3）如图②，过点B作DB⊥x轴交正比例函数y= x的图象于点D，连结AC，交正比例函数y= x的图象于点E，连结AD、CD．如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动，同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动．当其中一个点到达终点时，另一个点随之停止运动，连结PQ、QE、PE．设运动时间为t秒，是否存在某一时刻，使PE平分∠APQ，同时QE平分∠PQC？若存在，求出t的值；若不存在，请说明理由．          参考答案：一、选择题 B  A  D  A  A  D  C  D  A  A  C  B  C  二、填空题14. （2，1）              15. ﹣6                16. y=﹣x2+6x﹣11        17. 8  18. S=6x2+2x        19. ＜          20. ③④              21. ①④  三、解答题22. 解：（1）∵二次函数y=x2+2x+m的图象过点A（3，0）．
∴9+6+m=0，
∴m=﹣15；
（2）∵y=x2+2x﹣15=（x+1）2﹣16，
∴二次函数的图象的对称轴为x=﹣1，
∵a=1＞0，
∴当x＞﹣1时，函数值y随x的增大而增大．  23. 解：（1）A的坐标是（2，0），E的坐标是（1，2）．
设抛物线的解析式是y=ax2+bx+c，
根据题意得：，
解得：．
则抛物线的解析式是y=﹣2x2+4x；
（2）当△OAP的面积是2时，P的纵坐标是2或﹣2．
当﹣2x2+4x=2时，解得：x=1，则P的坐标是（1，2）；
当﹣2x2+4x=﹣2时，解得：x=1±，
此时P的坐标是（1+，﹣2）或（1﹣，﹣2）；
（3）AF=AB+BF=2+1=3．
OA=2，则A是直角顶点时，Q不可能在抛物线上；
当F是直角顶点时，Q不可能在抛物线上；
当Q是直角顶点时，Q到AF的距离是AF=，若Q存在，则Q的坐标是（2﹣，），即（﹣，），不在抛物线上，总之Q不存在．
 24. （1）解：∵抛物线y= x2﹣x+a其顶点在直线y=﹣2x上．
∴抛物线y= x2﹣x+a，
= （x2﹣2x）+a，
= （x﹣1）2﹣ +a，
∴顶点坐标为：（1，﹣ +a），
∴y=﹣2x，﹣ +a=﹣2×1，
∴a=﹣
（2）解：二次函数解析式为：y= x2﹣x﹣ ，
∵抛物线y= x2﹣x﹣ 与x轴交于点A，B，
∴0= x2﹣x﹣ ，
整理得：x2﹣2x﹣3=0，
解得：x=﹣1或3，
A（﹣1，0），B（3，0）
（3）解：作出平行四边形ACBD，作DE⊥AB，
在△AOC和△BDE中
∵
∴△AOC≌△BED（AAS），
∵AO=1，
∴BE=1，
∵二次函数解析式为：y= x2﹣x﹣ ，
∴图象与y轴交点坐标为：（0，﹣ ），
∴CO= ，∴DE= ，
D点的坐标为：（2， ），
∴点D关于x轴的对称点D′坐标为：（2，﹣ ），
代入解析式y= x2﹣x﹣ ，
∵左边=﹣ ，右边= ×4﹣2﹣ =﹣ ，
∴D′点在函数图象上．
 25. （1）解：∵点A（﹣2，0），B（3，0）在抛物线y= x2+bx+c上，
∴ ，
解得：b=﹣ ，c=﹣
（2）解：设点F在直线y= x上，且F（2， ）．
如答图1所示，过点F作FH⊥x轴于点H，则FH= ，OH=2，
∴tan∠FOB= = ，∴∠FOB=60°．

∴∠AOE=∠FOB=60°．
连接OC，过点C作CK⊥x轴于点K．
∵点A、C关于y= x对称，∴OC=OA=2，∠COE=∠AOE=60°．
∴∠COK=180°﹣∠AOE﹣∠COE=60°．
在Rt△COK中，CK=OC•sin60°=2× = ，OK=OC•cos60°=2× =1．
∴C（1，﹣ ）．
抛物线的解析式为：y= x2﹣ x﹣ ，当x=1时，y=﹣ ，
∴点C在所求二次函数的图象上
（3）解：假设存在．
如答图1所示，在Rt△ACK中，由勾股定理得：AC= = = ．
如答图2所示，∵OB=3，∴BD=3 ，AB=OA+OB=5．
在Rt△ABD中，由勾股定理得：AD= = =2 ．
∵点A、C关于y= x对称，
∴CD=AD=2 ，∠DAC=∠DCA，AE=CE= AC= ．
连接PQ、PE，QE，则∠APE=∠QPE，∠PQE=∠CQE．

在四边形APQC中，∠DAC+∠APQ+∠PQC+∠DCA=360°（四边形内角和等于360°），
即2∠DAC+2∠APE+2∠CQE=360°，
∴∠DAC+∠APE+∠CQE=180°．
又∵∠DAC+∠APE+∠AEP=180°（三角形内角和定理），
∴∠AEP=∠CQE．
在△APE与△CEQ中，∵∠DAC=∠DCA，∠AEP=∠CQE，
∴△APE∽△CEQ，
∴ ，即： ，
整理得：2t2﹣ t+3=0，
解得：t= 或t= （t＜ ，所以舍去）
∴存在某一时刻，使PE平分∠APQ，同时QE平分∠PQC，此时t=