2023年湖北省襄阳市宜城市中考适应性考试数学试题（含答案）

这是一份2023年湖北省襄阳市宜城市中考适应性考试数学试题（含答案），共15页。试卷主要包含了下列事件中，是必然事件的是等内容，欢迎下载使用。
宜城市2023年中考适应性考试
数 学 试 题
（本试题卷共6页，满分120分，考试时间120分钟）
★ 祝 考 试 顺 利 ★

注意事项：
1．答卷前，考生务必将自己的姓名、考试号填写在试题卷和答题卡上，并将考试号条形码粘贴在答题卡上指定位置．
2．选择题每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试题卷上无效．
3．非选择题（主观题）用0.5毫米的黑色签字笔直接答在答题卡上每题对应的答题区域内，答在试题卷上无效．作图一律用2B铅笔或0.5毫米的黑色签字笔．
4．考试结束后，请将本试题卷和答题卡一并上交．

一、选择题:(本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将其标号在答题卡上涂黑作答．)
1．－3的绝对值的相反数是（     ）
A．3 B． C．－3 D．
2．下列图形：等边三角形，等腰梯形，正方形，圆中，既是轴对称图形又是中心对称图形的有（     ）
A．1个 B．2个 C．3个 D．4个
3．下列计算正确的是（     ）
A． B．
C． D．
4．如图的几何体的左视图是（     ）
A.B.C.D.
5．已知反比例函数，当1＜x＜3时，y的取值范围是（     ）
A．2＜y＜0 B．1＜y＜3 C．2＜y＜6 D．6＜y＜2
6．下列事件中，是必然事件的是（     ）
A．任意画一个平行四边形，是中心对称图形
B．从0，1，2中任意抽取一个数字都是正数
C．抛掷1个骰子，掷得的结果不是1就是6
D．经过有交通信号灯的路口，遇到绿灯
7．如图，直线a∥b，∠1=39°，∠2=70°，则度数是（     ）
A．39° B．21° C．31° D．70°
8．如图，在△ABC中，∠B＝30°，以点A为圆心的圆与边BC相切于点D，与AC，AB分别交于点E和点G，点F是优弧GE上一点，∠GFE＝50°，则∠CDE的度数是（     ）
A．10° B．20° C．30° D．40°
9．七巧板是一种古老的中国传统智力玩具，如图，在正方形纸板ABCD中，BD为对角线，E，F分别为BC，CD的中点，分别交BD，EF于O，P两点，M，N分别为BO，DO的中点，连接MP，NF，沿图中实线剪开即可得到一副七巧板，则在剪开之前，关于该图形的下列说法：①图中的三角形都是等腰直角三角形；②图中的四边形MPEB是菱形；③四边形EFNB的面积占正方形ABCD面积的．正确的有（     ）
A. ①③ B. ①② C. 只有① D. ②③
10．如图，二次函数y＝ax2＋bx＋c的图象经过点(1，0)，对称轴是直线x＝－1，下列结论:
①abc＞0,② b2－4ac≥0 ,③2a－b＝0,④3a＋2c＜0中错误的个数是（     ）
A．1 B．2 C．3 D．4

二、填空题（本大题共6个小题，每小题3分，共18分）把答案填在答题卡的相应位置上．
11．截至北京时间4月14日6时30分，全球累计确诊新冠肺炎病例超过435万例．用科学记数法表示435万是 ．
12．若式子有意义，则的取值范围是 ．
13．一个不透明的袋子中装有红、白小球各两个，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球是一红一白的概率为 ．
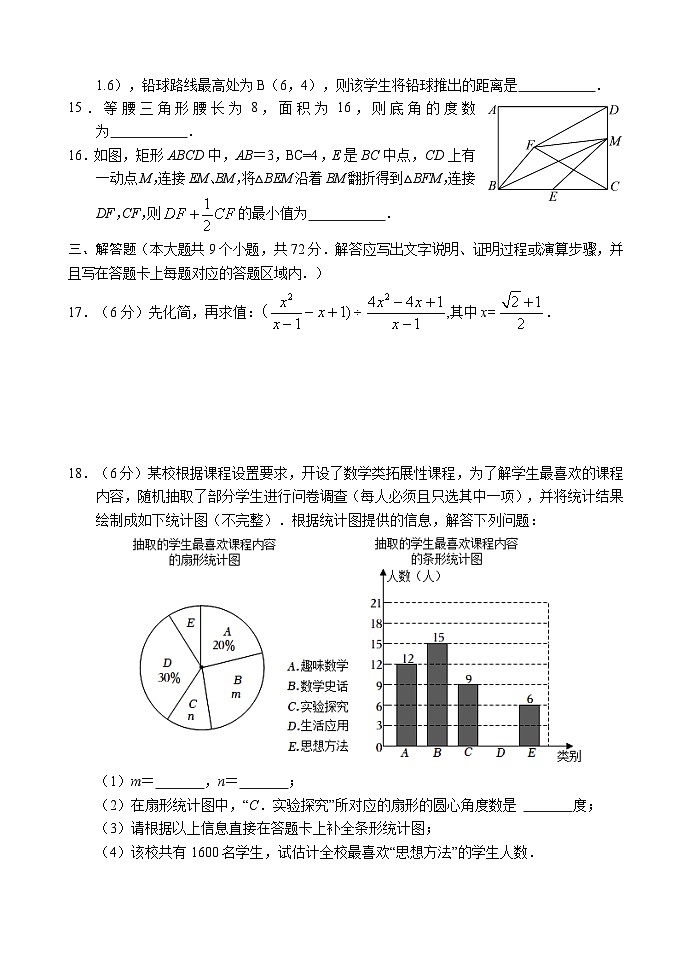
14．某学生推铅球，铅球所经过的路线是抛物线的一部分，若这名学生出手点A（0，1.6），铅球路线最高处为B（6，4），则该学生将铅球推出的距离是 ．
15．等腰三角形腰长为8，面积为16，则底角的度数为 ．
16．如图，矩形ABCD中，AB＝3，BC=4，E是BC中点，CD上有一动点M，连接EM、BM，将△BEM沿着BM翻折得到△BFM，连接DF，CF，则的最小值为 ．
三、解答题（本大题共9个小题，共72分．解答应写出文字说明、证明过程或演算步骤，并且写在答题卡上每题对应的答题区域内．）
17．（6分）先化简，再求值：,其中x=．






18．（6分）某校根据课程设置要求，开设了数学类拓展性课程，为了解学生最喜欢的课程内容，随机抽取了部分学生进行问卷调查（每人必须且只选其中一项），并将统计结果绘制成如下统计图（不完整）．根据统计图提供的信息，解答下列问题：

（1）m＝　 　，n＝　 　；
（2）在扇形统计图中，“C．实验探究”所对应的扇形的圆心角度数是 　 　度；
（3）请根据以上信息直接在答题卡上补全条形统计图；
（4）该校共有1600名学生，试估计全校最喜欢“思想方法”的学生人数．



19．（6分）如图，小明想要利用无人机测量他家附近一座古塔（AB）的高度．在古塔所在的地平面上选定点C．在C处测得古塔顶端A点的仰角为53°，小明遥控无人机悬停在点C正上方的D处时，测得古塔顶端A点的俯角为26.6°，若观测点到古塔的水平距离（BC）为30m，求古塔（AB）的高度以及无人机离地面的高度（CD）．（参考数据：tan26.6°≈0.5，sin37°＝cos53°≈0.6，tan37°≈0.75）











20．（6分）如图，在矩形中，，
（1）作∠BAC 的角平分线，交BC于点E；
（2）求的周长．




21．（7分）已知关于x的一元二次方程x2－4x+m+1＝0有实数根．
（1）求m的取值范围；
（2）如果方程的两个实数根为x1，x2，且，求m的所有整数值的和．







22．（8分）如图，PA是⊙O的切线，A是切点，AC是⊙O的直径，点B是⊙O的上一点，且OP∥BC，OP交⊙O于点D.
（1）求证：PB是⊙O的切线；
（2）若AC=OP=4，求阴影部分的面积.








23．（10分）“五·一”前夕，某蛋糕店推出A、B两种不同口味的蛋糕．3个A种蛋糕和5个B种蛋糕的利润和为380元，5个A种蛋糕和3个B种蛋糕的利润和为420元．
（1）求每个A种蛋糕和B种蛋糕的利润；
（2）蛋糕店计划每天制作两种蛋糕共50个，设制作A种蛋糕x个，两种蛋糕全部卖完共获利y元．
①求y与x之间的函数关系式；
②若每天制作A种蛋糕的个数不少于30个，且不超过B种蛋糕个数的4倍，求每天全部卖完这两种蛋糕获得的最大利润；
（3）在（2）的条件下，该蛋糕店对A种蛋糕以每个优惠a（5≤a≤15）元的价格进行“五·一”促销活动，B种蛋糕价格不变，且每天全部卖完这两种蛋糕所获得的最大利润不低于2240元，请求出a的取值范围．​









24．（11分） 已知菱形ABCD的边长为4．∠ADC=60°，等边△AEF两边分别交边DC，CB于点E，F．
（1）特殊发现：如图1，若点E，F分别是边DC，CB的中点．求证：菱形ABCD对角线AC，BD的交点O即为等边△AEF的外心；
（2）若点E，F始终分别在边DC，CB上移动，等边△AEF的外心为点P．
①猜想验证：如图2．猜想△AEF的外心P落在哪条直线上，并加以证明；
②学以致用：如图3，当△AEF的面积最小时，过点P任作一直线分别交边DA于点M，交边DC的延长线于点N，求的值．


25．（12分）如图，在平面直角坐标系中，直线y＝－x－2与x轴交于点A，与y轴交于点B，抛物线y＝－(x－m)2＋m2的顶点为P，过点P分别作x轴，y轴的垂线交AB于点M，Q，直线PM交x轴于点N．
（1）若点P在y轴的左侧，且N为PM中点，求抛物线的解析式；
（2）求线段PQ长的最小值，并求出当PQ的长度最小时点P的坐标；
（3）若P，M，N三点中，任意两点都不重合，且PN＞MN，求m的取值范围．










评分标准
一、选择题:(本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将其标号在答题卡上涂黑作答．)
  CBDADACBCB 
二、填空题（本大题共6个小题，每小题3分，共18分）把答案填在答题卡的相应位置上．
11.（4.35×106） 12.（） 13.（）
14.（） 15.（75°或15°） 16.()

三、解答题（本大题共9个小题，共72分．解答应写出文字说明、证明过程或演算步骤，并且写在答题卡上每题对应的答题区域内．）
17.（6分）
解：原式=
=
=…………………………………4分

当时，原式=…………………………………6分
18.（6分）
解：（1）25%，15%；…………………………………2分
（2）54；…………………………………3分
（3）D类别人数为60×30%＝18（人），
补全图形如下：
…………………………………5分
（4）根据题意得：1600×＝160（名），
答：估计全校最喜欢“数学史话”的学生人数有160名．……………………………6分

19.（6分）
解：过点A作AE⊥CD于E，由图可知，AE＝BC=30m，AB=CE．
∠BCD＝90°……1分
在Rt△ACE中，∠ACE＝90°﹣∠ABC＝37°，
∴.…………………2分
∴.…………………3分
在Rt△ADE中，∠DAE＝26.6°，，
∴.……………4分
∵CD＝DE+EC，
∴．…………………5分
答：古塔的高度为40m，无人机离地面的高度位55m.…………6分

20.（6分）
解：(1)如图，射线AE即为所求.…………2分
作EF⊥AC于点F，
∵四边形ABCD是矩形，∴∠B=∠AFE=90°．
∵AE是∠BAC的角平分线，
∴∠BAE=∠FAE．
∴△ABE≌△AFE．∴AB=AF，BE=FE．…………3分
设BE=x，则FE=x，
∵，∴．
∴FC=10-6=4，．…………4分
在Rt△PEC中，，
∴，解得．
∴．…………5分
∴．∴．
∴．…………6分



21.（7分）
解：（1）根据题意得Δ＝（﹣4）2﹣4（m+1）≥0，
解得m≤3；…………3分
（2）由一元二次方程的根与系数的关系得x1+x2＝4，x1x2＝m+1.…………4分
∵，即.
∴m+1-4+1≥-1，解得m≥1，…………5分
∵m≤3，∴1≤m≤3．…………6分
∴m的整数值为1，2和3，它们的和=1+2+3=6．…………7分

22.（8分）
（1）证明：连接OB，
∵PA是⊙O的切线，
∴∠PAO=90°.……………………………………1分
∵OP∥BC,
∴∠AOP=∠ACB，∠POB=∠OBC.
∵OC=OB，∴∠OBC=∠OCB.
∴∠AOP=BOP.
∵OA=OB，OP=OP，
∴△PAO≌△PBO.………………………………2分
∴∠PBO=∠PAO=90°.…………………………3分
又∵OB是⊙O的半径，
∴PB是⊙O的切线； ……………………………4分
（2）解：连接AD
∵AC=OP，OD=AC，∴OD=OP.
∵∠PAO=90°,∴AD=OP=OD=OA.………………5分
∴△AOD是等边三角形，∴∠AOD=60°.∴∠AOB=120°.……………………6分
在Rt△AOP中，,……………………7分
∴……………8分



23.（10分）​
解：（1）设每个A种蛋糕的利润为m元、每个B种蛋糕的利润为n元；
根据题意，得，解得.
答：每个A种蛋糕的利润为60元、每个B种蛋糕的利润为40元；………………3分
（2）①由题意知，y＝60x+40（50﹣x）＝20x+2000，
∴y与x之间的函数关系式为y＝20x+2000；………………………5分
②由题意得，，∴
又∵，∴30≤x≤40，
在y＝20x+2000中，
∵20＞0，∴y随x的增大而增大，
∴当x＝40时，y取得最大值，最大值为20×40+2000＝2800，
即最大利润为2800元；………………………7分
（3）在（2）的条件下30≤x≤40，总利润y＝（20﹣a）x+2000，………………8分
∵5≤a≤15，
∴20﹣a＞0，
∴y随x的增大而增大，
∴x＝40，y有最大值，
∴40（20﹣a）+2000≥2240，解得a≤14；
∴5≤a≤14
∴a的取值范围值为5≤a≤14．………………………10分
24. （11分）
（1）证明：如图1，连接OE、0F，
∵四边形ABCD是菱形，∴AC⊥BD，BD平分∠ADC，AD=DC=BC.…………1分
∴∠COD=∠COB=∠AOD=90°，.…………2分
又∵E、F分别为DC、CB中点，：
.…………3分
.
∴点O为△AEF的外心.………………4分
（2）解：①猜想：外心P一定落在直线DB上．理由如下：
如图2，分别连接PE、PA，过点P分别作PI⊥CD于I，PJ⊥AD于J，
∴∠PIE=∠PJD=90°.…………5分
∵∠ADC=60°，∴∠IPJ=360°-∠PIE-∠PJD-∠JDI=120°.
∵点P是等边△AEF的外心，∴∠EPA=120°，PE=PA.……6分
∴∠IPJ=∠EPA.∴∠IPE=∠JPA.
∴△PIE≌△PJA.…………7分
∴PI=PJ.∴点P在∠ADC的平分线上，即点P落在直线DB上；………………8分
②当AE⊥DC时．△AEF面积最小，此时点E、F分别为DC、CB中点．
连接BD、AC交于点P，由（1）可得点P即为△AEF的外心．
如图3．设MN交BC于点G，
设DM=x，DN=y（x≠0．y≠O），则CN=y-4，
∵BC∥DA，∴△GBP≌△MDP．∴BG=DM=x．∴CG=4-x.………9分
∵BC∥DA，∴△NCG∽△NDM，
∴.…………10分
∴.∴，
∴.即．………………11分
25．（12分）
解：（1）∵抛物线y＝－(x﹣m)2＋m2的顶点为P，∴P（m，m2），
∵PM⊥x轴，∴M（m，－m－2），N（m，0），
∵N为PM中点，∴m2－m－2＝0，
解得m1＝－1，m2＝2，
∵点P在y轴左侧，∴m＝－1，
∴抛物线的解析式为y＝－(x＋1)2＋1．……………4分
（2）由y＝－x－2＝0，解得x＝－2，所以A（－2，0），OA＝2．
当x＝0时，y＝－x－2＝－2，所以B（0，－2），OB＝OA＝2．
∵∠AOB＝90°，∴∠OAB＝∠OBA＝45°，
∵PM⊥x轴，PQ⊥y轴，∴∠PQM＝∠PMQ＝45°，
∴PQ＝PM＝m2－(－m－2)＝(m＋)2＋．
∵a＝1＞0，∴当m＝－时，PQ的值最小，最小值为，
此时点P的坐标为（－，）．……………8分
（3）易知，当m＝－2时，M，N重合，不合题意；
当m＝0时，P，N重合，不合题意；
当m＜－2时（如图），PN＞MN，符合题意；
当m＞－2时（如图），PN－MN＝m2－[－(－m－2)]＝m2－m－2＝(m－)2－．
由m2－m－2＝0，解得m1＝－1，m2＝2，
又∵a＝1＞0，∴当－2＜m＜－1或m＞2时，PN－MN的值大于0，即PN＞MN；
综上可知，m的取值范围是m＜－2或－2＜m＜－1或m＞2．……………12分