真题重组卷03——2023年中考数学真题汇编重组卷（安徽专用）

这是一份真题重组卷03——2023年中考数学真题汇编重组卷（安徽专用），文件包含真题重组卷03-2023年中考数学真题汇编重组卷安徽专用解析版docx、真题重组卷03-2023年中考数学真题汇编重组卷安徽专用原卷版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
绝密★启用前
冲刺2023年中考数学精选真题重组卷03
数 学（安徽专用）
注意事项：
1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（本大题共10小题，每小题4分，满分40分）
1．（2022·江苏淮安·统考中考真题）的相反数是(    )
A． B． C． D．
【答案】B
【分析】根据相反数的定义即可求解．相反数的定义是：如果两个数只有符号不同，我们称其中一个数为另一个数的相反数，特别地，的相反数还是．
【详解】解：的相反数是，
故选：B．
【点睛】本题考查了相反数的定义，掌握相反数的定义是解题的关键．
2．（2022·辽宁锦州·统考中考真题）党的十八大以来，以习近平同志为核心的党中央重视技能人才的培育与发展．据报道，截至2021年底，我国高技能人才超过60000000人，请将数据60000000用科学记数法表示为（    ）
A． B． C． D．
【答案】B
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于或等于10时，n是正整数；当原数的绝对值小于1时，n是负整数．
【详解】解：将数据60000000用科学记数法表示为；
故选B．
【点睛】本题主要考查科学记数法，熟练掌握科学记数法是解题的关键．
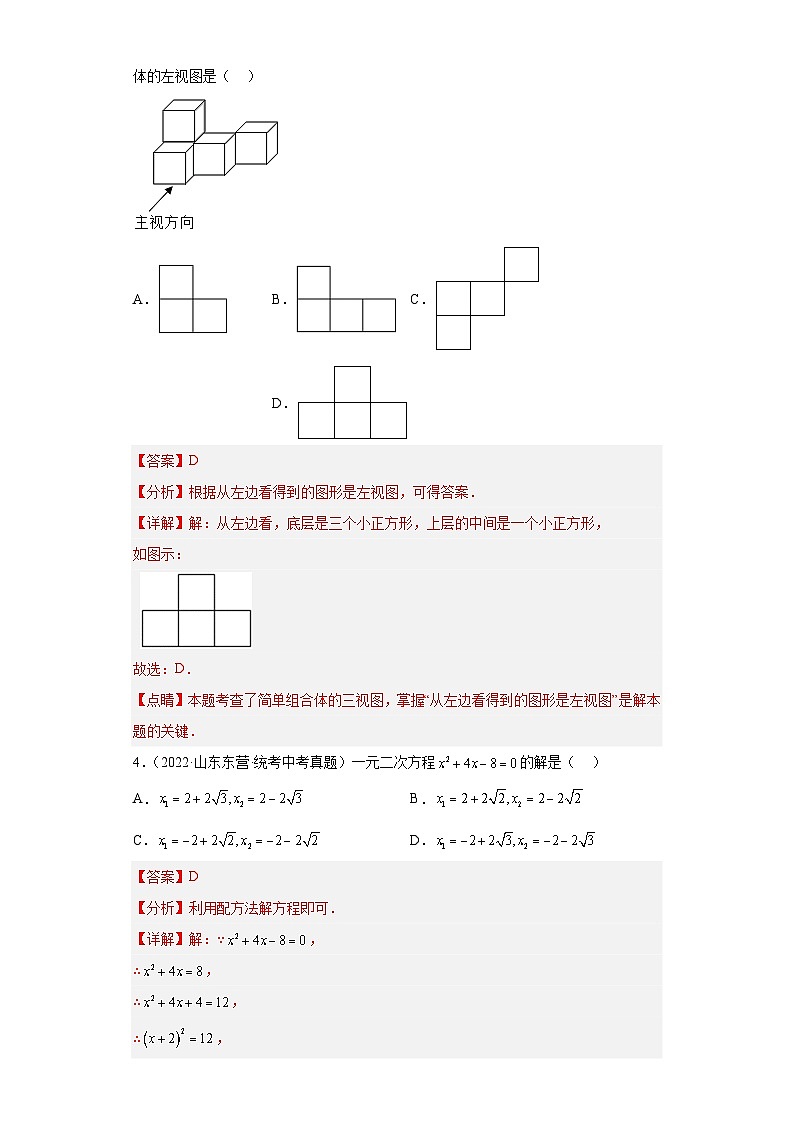
3．（2022·内蒙古·中考真题）由5个相同的小正方体组成的几何体，如图所示，该几何体的左视图是（    ）

A． B． C． D．
【答案】D
【分析】根据从左边看得到的图形是左视图，可得答案．
【详解】解：从左边看，底层是三个小正方形，上层的中间是一个小正方形，
如图示：

故选：D．
【点睛】本题考查了简单组合体的三视图，掌握“从左边看得到的图形是左视图”是解本题的关键．
4．（2022·山东东营·统考中考真题）一元二次方程的解是（    ）
A． B．
C． D．
【答案】D
【分析】利用配方法解方程即可．
【详解】解：∵，
∴，
∴，
∴，
∴，
解得，
故选D．
【点睛】本题主要考查了解一元二次方程，熟知解一元二次方程的方法是解题的关键．
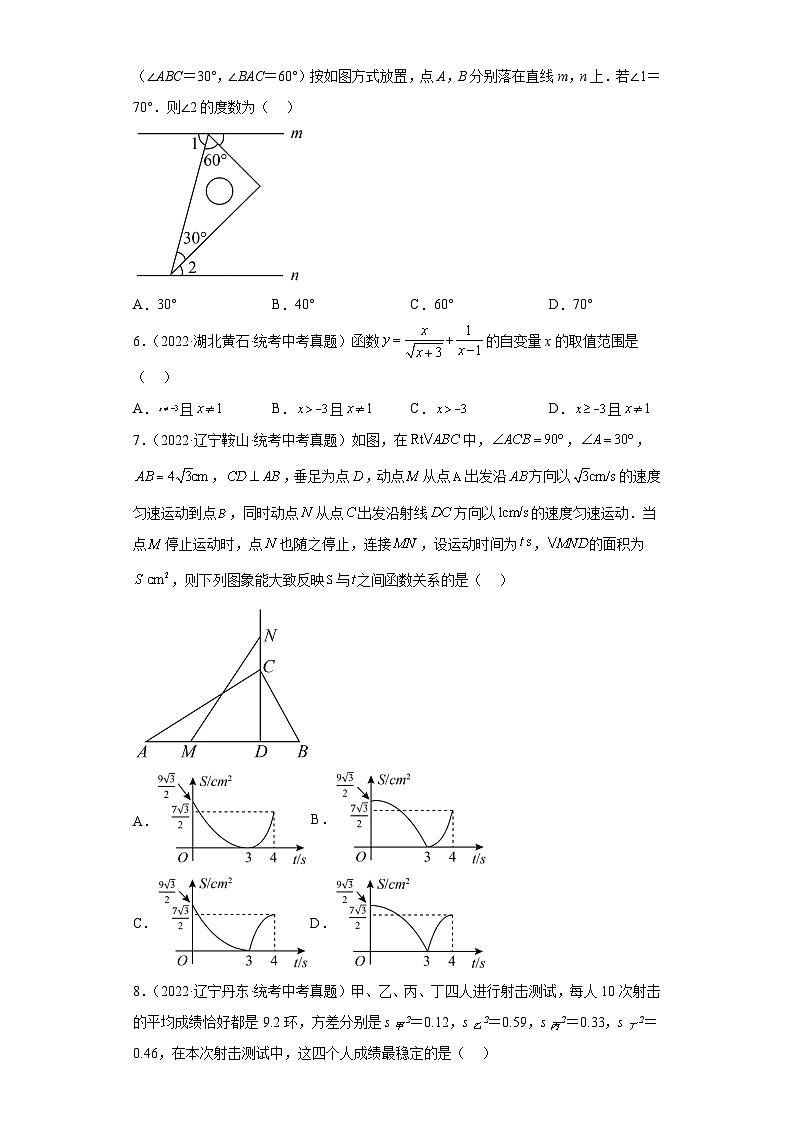
5．（2022·湖北襄阳·统考中考真题）已知直线m∥n，将一块含30°角的直角三角板ABC（∠ABC＝30°，∠BAC＝60°）按如图方式放置，点A，B分别落在直线m，n上．若∠1＝70°．则∠2的度数为（    ）

A．30° B．40° C．60° D．70°
【答案】B
【分析】根据平行线的性质求得∠ABD，再根据角的和差关系求得结果．
【详解】解：∵mn，∠1=70°，
∴∠1=∠ABD=70°，
∵∠ABC=30°，
∴∠2=∠ABD-∠ABC=40°，

故选：B．
【点睛】本题主要考查了平行线的性质，关键是熟练掌握平行线的性质．
6．（2022·湖北黄石·统考中考真题）函数的自变量x的取值范围是（    ）
A．且 B．且 C． D．且
【答案】B
【分析】直接利用二次根式有意义的条件、分式有意义的条件分析得出答案．
【详解】解：依题意，
∴且
故选B
【点睛】此题主要考查了函数自变量的取值范围，正确掌握二次根式与分式有意义的条件是解题关键．
7．（2022·辽宁鞍山·统考中考真题）如图，在中，，，，，垂足为点，动点从点出发沿方向以的速度匀速运动到点，同时动点从点出发沿射线方向以的速度匀速运动．当点停止运动时，点也随之停止，连接，设运动时间为，的面积为，则下列图象能大致反映与之间函数关系的是（    ）

A． B． C． D．
【答案】B
【分析】分别求出M在AD和在BD上时△MND的面积为S关于t的解析式即可判断．
【详解】解：∵∠ACB＝90°，∠A＝30°，，
∴∠B＝60°，，，
∵CD⊥AB，
∴，，，
∴当M在AD上时，0≤t≤3，
，，
∴，
当M在BD上时，3＜t≤4，
，
∴，
故选：B．
【点睛】本题考查了动点问题的函数图象，函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．
8．（2022·辽宁丹东·统考中考真题）甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好都是9.2环，方差分别是s甲2＝0.12，s乙2＝0.59，s丙2＝0.33，s丁2＝0.46，在本次射击测试中，这四个人成绩最稳定的是（    ）
A．甲 B．乙 C．丙 D．丁
【答案】A
【分析】根据方差的定义，方差越小数据越稳定．进行判断即可．
【详解】解：∵s甲2＝0.12，s乙2＝0.59，s丙2＝0.33，s丁2＝0.46，
∴s甲2＜s丙2＜s丁2＜s乙2，
∴成绩最稳定的是甲，
故选：A．
【点睛】本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
9．（2022·山东枣庄·统考中考真题）在践行“安全在我心中，你我一起行动”主题手抄报评比活动中，共设置“交通安全、消防安全、饮食安全、防疫安全”四个主题内容，推荐两名学生参加评比，若他们每人从以上四个主题内容中随机选取一个，则两人恰好选中同一主题的概率是（　　）
A． B． C． D．
【答案】D
【分析】设“交通安全、消防安全、饮食安全、防疫安全”四个主题内容分别为A、B、C、D，画出树状图进行求解即可．
【详解】解：设“交通安全、消防安全、饮食安全、防疫安全”四个主题内容分别为A、B、C、D，画树状图如下：

共有16种等可能的结果，两人恰好选中同一主题的结果有4种，
则两人恰好选中同一主题的概率为．
故选：D．
【点睛】本题考查了列表法与树状图法求概率，读懂题意，画出树状图是解题的关键．
10．（2022·山东日照·统考中考真题）《孙子算经》是中国传统数学的重要著作，其中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺．木长几何？”意思是：用一根绳子去量一根木头的长，绳子还剩余4.5尺；将绳子对折再量木头，则木头还剩余1尺，问木头长多少尺？可设木头长为x尺，绳子长为y尺，则所列方程组正确的是（    ）
A． B．
C． D．
【答案】D
【分析】设木头长为x尺，绳子长为y尺，根据“用一根绳子去量一根木头的长，绳子还剩余4.5尺；将绳子对折再量木头，则木头还剩余1尺”，即可得出关于x，y的二元一次方程组，此题得解．
【详解】解：设木头长为x尺，绳子长为y尺，
由题意可得．
故选：D．
【点睛】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．

二、填空题
11．（2022·湖南益阳·统考中考真题）已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m2﹣n2的值是 _____．
【答案】3
【分析】观察已知和所求可知，，将代数式的值代入即可得出结论．
【详解】解：∵2m+n＝3，2m﹣n＝1，
∴，
故答案为：3．
【点睛】本题主要考查代数式求值，平方差公式的应用，熟知平方差公式的结构是解题关键．
12．（2022·四川绵阳·统考中考真题）因式分解：_________．
【答案】
【分析】先提取公因式，然后根据平方差公式因式分解即可求解．
【详解】解：原式＝．
故答案为：．
【点睛】本题考查了因式分解，正确的计算是解题的关键．
13．（2022·辽宁·统考中考真题）如图，矩形OABC的顶点B在反比例函数y＝（x＞0）的图像上，点A在x轴的正半轴上，AB＝3BC，点D在x轴的负半轴上，AD＝AB，连接BD，过点A作AE∥BD交y轴于点E，点F在AE上，连接FD，FB．若△BDF的面积为9，则k的值是_______．

【答案】6
【分析】根据△BDF的面积等于△ABD的面积，设B（a，3a）（a＞0），则×3a•3a＝9，求解即可得到点的坐标，则根据求解即可．
【详解】解：∵AE∥BD，依据同底等高的原理，
∴△BDF的面积等于△ABD的面积，
∵AB＝3BC，AD＝AB，
∴设B（a，3a）（a＞0），则×3a•3a＝9，
解得a＝，
∴3a2＝6．
即k＝6．
故答案为：6．
【点睛】本题考查了反比例函数系数的几何意义，解题的关键是利用同底等高的原理将原图形转换成面积相等的其他图像，从而得到反比例函数图像上的点的坐标，然后利用求解．
14．（2022·贵州贵阳·统考中考真题）如图，在四边形中，对角线，相交于点，，．若，则的面积是_______，_______度．

【答案】     ##    
【分析】通过证明，利用相似三角形的性质求出，，再利用勾股定理求出其长度，即可求三角形ABE的面积，过点E作EF⊥AB，垂足为F，证明是等腰直角三角形，再求出，继而证明，可知，利用外角的性质即可求解．
【详解】
，
，
，
，
设，
，
，
，
在中，由勾股定理得，
，
解得或，
对角线，相交于点，
，
，
，
，
过点E作EF⊥AB，垂足为F，
，
，
，
，
，
，
，
故答案为：，．
【点睛】本题考查了相似三角形的判定和性质，勾股定理，等腰直角三角形的判定和性质，全等三角形的判定和性质及三角形外角的性质，熟练掌握知识点是解题的关键．

三、解答题
15．（2022·四川广安·统考中考真题）计算：
【答案】0
【分析】根据零指数幂、绝对值的意义、特殊角的三角函数值、负整数指数幂，二次根式的加减运算进行计算，即可得到答案．
【详解】解：
=
=0；
【点睛】本题考查了零指数幂、绝对值的意义、特殊角的三角函数值、负整数指数幂，二次根式的加减运算，解题的关键是掌握运算法则，正确的进行计算．
16．（2022·四川广安·统考中考真题）先化简：，再从0、1、2、3中选择一个适合的数代人求值．
【答案】x；1或者3

【分析】根据分式的混合运算法则即可进行化简，再根据分式有意义的条件确定x可以选定的值，代入化简后的式子即可求解．
【详解】




根据题意有：，，
故，，
即在0、1、2、3中，
当x=1时，原式=x=1；
当x=3时，原式=x=3．
【点睛】本题主要考查了运用分式的混合运算法则将分式的化简并求值、分式有意义的条件等知识，熟练掌握分式的混合运算法则是解题的关键．
17．（2022·安徽滁州·校考一模）【阅读】求值…．
解：设S= …①
将等式①的两边同时乘以2得：2S= …②
由②﹣①得：
即：S= …
【运用】仿照此法计算：
…；
【延伸】如图，将边长为1的正方形分成4个完全一样的小正方形，得到左上角一个小正方形为S1，选取右下角的小正方形进行第二次操作，又得到左上角更小的正方形S2，依次操作2019次，依次得到小正方形S1、S2、S3、…、S2019．
完成下列问题：
（1）小正方形的面积S2019等于　 　；
（2）求正方形S1、S2、S3、…、S2019的面积和．

【答案】[运用] ；（1）；（2）
【分析】[运用]仿照题目中的算法可以解答本题；
（1）由、、，可得；
（2）仿照题目中的算法可以解答本题．
【详解】解：[运用]设①，
①，得：②，
②①，得：，
则，即；
（1）、、，
∴，
故答案为：；
（2）设①，
①，得：②，
①-②，得：，
所以，即．
【点睛】本题考查数字的变化类，解题的关键是明确题意，发现数字的变化规律．
18．（2022·安徽滁州·校考一模）如图，在平面直角坐标系中，各顶点的坐标分别是，与关于原点位似，的对应点分别为，其中的坐标是．

(1)和的相似比是 ；
(2)请画出；
(3)边上有一点，在边上与点对应点的坐标是 ；
(4)的面积是 ．
【答案】(1)
(2)见解析
(3)
(4)3

【分析】（1）直接利用点对应点坐标，即可得出相似比；
（2）利用相似比即可得出对应点位置，进而确定答案；
（3）直接利用位似图形的性质得出点坐标即可；
（4）利用三角形面积公式求解即可．
【详解】（1）解：和的相似比是；
故答案为：；
（2）如图所示，即为所求；

（3）边上有一点，在边上与点对应点的坐标是；
故答案为：；
（4）的面积是：．
故答案为：3．
【点睛】本题主要考查了位似变换以及三角形面积求法，正确得出对应点位置是解题关键．
19．（2022·内蒙古呼和浩特·统考中考真题）“一去紫台连朔漠，独留青冢向黄昏”，美丽的昭君博物院作为著名景区现已成为外地游客到呼和浩特市旅游的打卡地．如图，为测量景区中一座雕像的高度，某数学兴趣小组在处用测角仪测得雕像顶部的仰角为，测得底部的俯角为．已知测角仪与水平地面垂直且高度为1米，求雕像的高．（用非特殊角的三角函数及根式表示即可）

【答案】米
【分析】过点作于，则四边形是矩形，则，在与中，分别表示出，根据即可求解．
【详解】如图，过点作于，则四边形是矩形，

，
中，，
，
中，，

，
（米）
答：雕像的高为米
【点睛】本题考查了解直角三角形的实际应用，掌握直角三角形中的边角关系是解题的关键．
20．（2022·内蒙古呼和浩特·统考中考真题）如图，在中，，以为直径的⊙交于点，交线段的延长线于点，连接．

(1)求证：；
(2)若，，求．
【答案】(1)证明见详解
(2)

【分析】（1）连接AD，由AB为直径可得AD⊥BC，再根据等腰三角形的三线合一性质即可证明结论．
（2）由（1）可得CD=4，BC=8，根据即可求得，进而利用勾股定理即可求得AC，由为⊙的直径，得∠BEC=∠ADC=90°，∠C为公共角，可得，根据三角形相似的性质即可求得CE，进而可求解．
（1）
证明：连接AD，如图所示：

∵为⊙的直径，
∴AD⊥BC，
又∵，
∴三角形ABC为等腰三角形，
∴AD为BC的垂直平分线，
∴BD=CD．
（2）
由（1）可得BD=CD=4，
，BC=2BD=8，
，
在Rt△ACD中，
，
又∵为⊙的直径，
∴∠BEC=∠ADC=90°，且∠C=∠C，
∴，
，即，
，
．
【点睛】本题考查了三角形与圆的综合问题，考查了等腰三角形的判定及性质、圆周角定理、相似三角形的判定及性质、锐角三角函数及勾股定理的应用，熟练掌握等腰三角形三线合一的性质及三角形相似对应边成比例的性质是解题的关键．
21．（2022·江苏常州·统考中考真题）为减少传统塑料袋对生态环境的破坏，国家提倡使用可以在自然环境下（特定微生物、温度、湿度）较快完成降解的环保塑料袋．调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查，使用情况为（不使用）、（1~3个）、（4~6个）、（7个及以上），以下是根据调查结果绘制的统计图的一部分．

(1)本次调查的样本容量是_____，请补全条形统计图；
(2)已知该小区有1500户家庭，调查小组估计：该小区1周内使用7个及以上环保塑料袋的家庭约有225户．调查小组的估计是否合理？请说明理由．
【答案】(1)100，图见解析
(2)合理，理由见解析

【分析】（1）利用频数除以频率即可得出，结合条形统计图及扇形统计图，求出涉及的户数再画图即可；
（2）利用样本估计总体的思想来解释即可．
【详解】（1）解：本次调查的样本容量为：（户），
使用情况的户数为：（户），
占的比例为：，
的比例为：，
使用情况的户数为：（户），
补全条形统计图如下：

故答案为：100．
（2）解：合理，理由如下：
利用样本估计总体：占的比例为：，
（户），
调查小组的估计是合理的．
【点睛】本题考查了形统计图及扇形统计图，样本估计总体，解题的关键是通过数形结合对数据进行分析．
22．（2022·四川内江·统考中考真题）如图，在矩形ABCD中，AB＝6，BC＝4，点M、N分别在AB、AD上，且MN⊥MC，点E为CD的中点，连接BE交MC于点F．

(1)当F为BE的中点时，求证：AM＝CE；
(2)若＝2，求的值；
(3)若MN∥BE，求的值．
【答案】(1)见解析
(2)
(3)

【分析】(1)根据矩形的性质，证明△BMF≌ △ECF，得BM＝CE，再利用点E为CD的 中点，即可证明结论；
(2)利用△BMF∽△ECF，得，从而求出BM的长，再利用△ANM∽△BMC ，得 ，求出AN的长，可得答案；
(3)首先利用同角的余角相等得 ∠CBF＝ ∠CMB，则tan∠CBF＝tan∠CMB，得 ，可得BM的长，由（2）同理可得答案．
【详解】（1）证明：∵F为BE的中点，
∴BF＝EF，
∵四边形ABCD是矩形，
∴AB∥CD，AB＝CD
∴∠BMF＝∠ECF，
∵∠BFM＝∠EFC，
∴△BMF≌△ECF（AAS），
∴BM＝CE，
∵点E为CD的中点，
∴CE＝CD，
∵AB＝CD，
∴，
∴，
∴AM＝CE；
（2）∵∠BMF＝∠ECF，∠BFM＝∠EFC，
∴△BMF∽△ECF，
∴，
∵CE＝3，
∴BM＝，
∴AM＝，
∵CM⊥MN，
∴∠CMN＝90°，
∴∠AMN+∠BMC＝90°，
∵∠AMN+∠ANM＝90°，
∴∠ANM＝∠BMC，
∵∠A＝∠MBC，
∴△ANM∽△BMC，
∴，
∴，
∴，
∴DN＝AD﹣AN＝4﹣＝，
∴；
（3）∵MN∥BE，
∴∠BFC＝∠CMN，
∴∠FBC+∠BCM＝90°，
∵∠BCM+∠BMC＝90°，
∴∠CBF＝∠CMB，
∴tan∠CBF＝tan∠CMB，
∴，
∴，
∴，
∴，
由（2）同理得，，
∴，
解得：AN＝，
∴DN＝AD﹣AN＝4﹣＝，
∴．
【点睛】本题是相似形综合题，主要考查了矩形的性质，全等三角形的判定与性质，相似三角形的判定与性质，三角函数等知识，求出BM的长是解决（2）和（3）的关键．
23．（2022·广西·中考真题）已知抛物线经过A（－1，0）、B（0、3）、 C（3，0）三点，O为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM ，交BC于点F

(1)求抛物线的表达式；
(2)求证：∠BOF＝∠BDF ：
(3)是否存在点M使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长
【答案】(1)
(2)见解析
(3)存在，或

【分析】（1）设抛物线的表达式为，将A（－1，0）、B（0、3）、C（3，0）代入，直接利用待定系数法求解即可；
（2）由正方形的性质可得，即可证明，根据全等三角形的性质即可求证；
（3）分别讨论：当点M在线段BD的延长线上时，当点M在线段BD上时，依次用代数法和几何法求解即可．
【详解】（1）设抛物线的表达式为，
将A（－1，0）、B（0、3）、C（3，0）代入，
得，解得，
抛物线的表达式为；
（2）四边形OBDC是正方形，
，
，
，
；
（3）存在，理由如下：
当点M在线段BD的延长线上时，此时，
，
设，
设直线OM的解析式为，
，
解得，
直线OM的解析式为，
设直线BC的解析式为，
把B（0、3）、 C（3，0）代入，得，
解得，
直线BC的解析式为，
令，解得，则，
，
四边形OBDC是正方形，
，
，
，
，
，
解得或或，
点M为射线BD上一动点，
，
，
，
当时，解得或，
，
．
当点M在线段BD上时，此时，，

，
，
，
由（2）得，
四边形OBDC是正方形，
，
，
，
，
，
，
，
，
；
综上，ME的长为或．
【点睛】本题考查了待定系数法求二次函数解析式，求一次函数解析式，正方形的性质，全等三角形的判定和性质，解直角三角形等，熟练掌握知识点是解题的关键．