


专题04 立体几何-冲刺高考数学大题突破+限时集训(新高考专用)
展开专题04 立体几何
立体几何一般作为全国卷第20题21题.重点题型主要是
1 体积问题及表面积问题
2 线面距离及线面角问题
3 二面角问题
4 空间几何综合问题
题型一:体积及表面积问题
1.在如图所示的多面体ABCDE中,平面ABC,,,,.
(1)证明:平面平面BDE;
(2)求多面体ABCDE的体积.
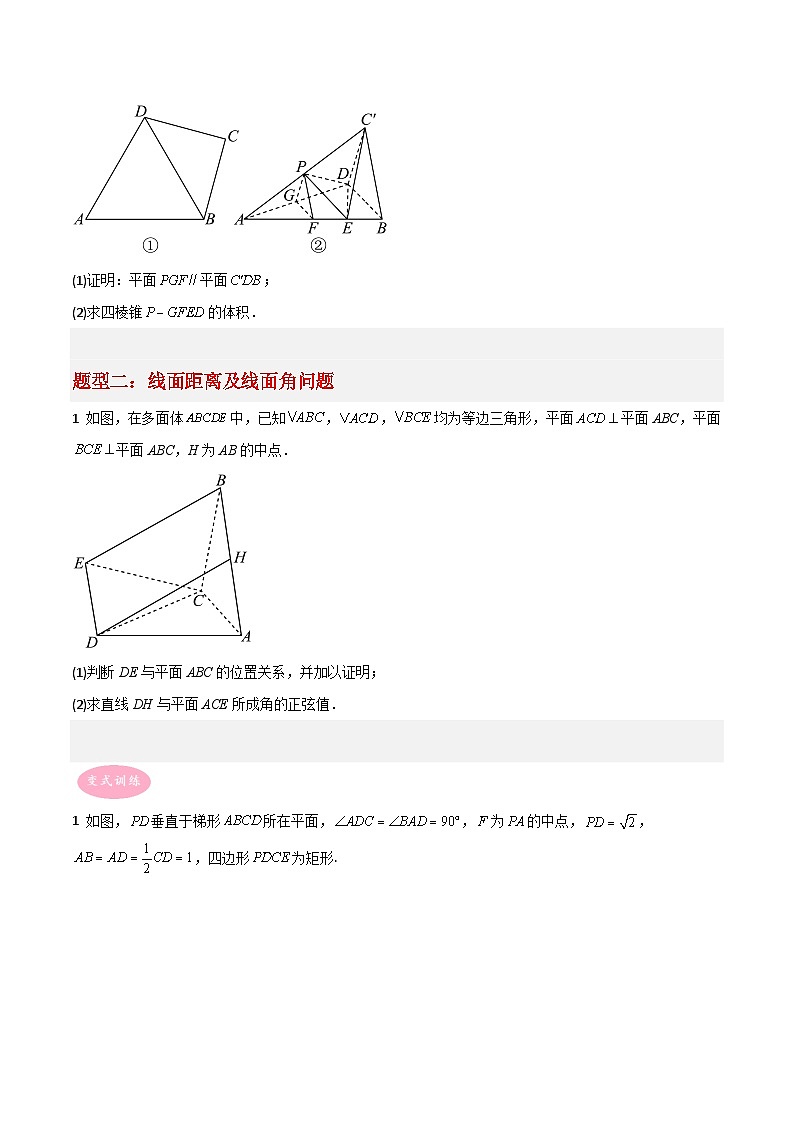
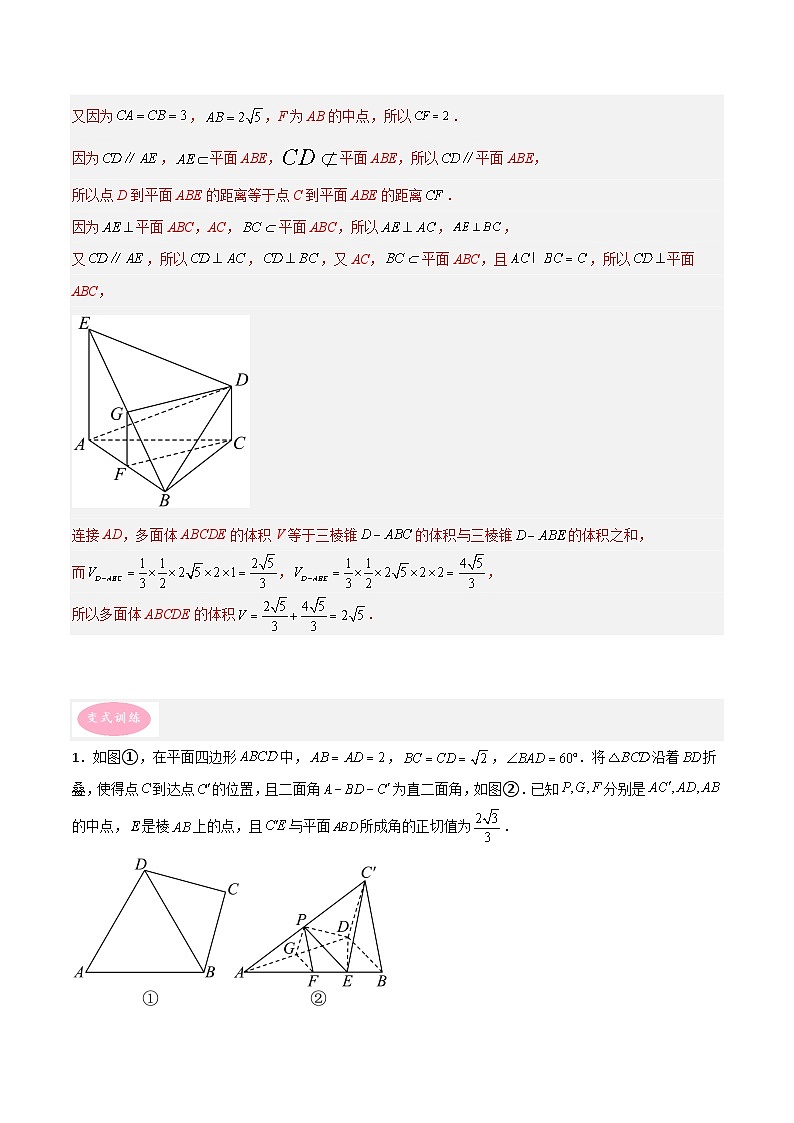
1.如图①,在平面四边形中,,,.将沿着折叠,使得点到达点的位置,且二面角为直二面角,如图②.已知分别是的中点,是棱上的点,且与平面所成角的正切值为.
(1)证明:平面平面;
(2)求四棱锥的体积.
题型二:线面距离及线面角问题
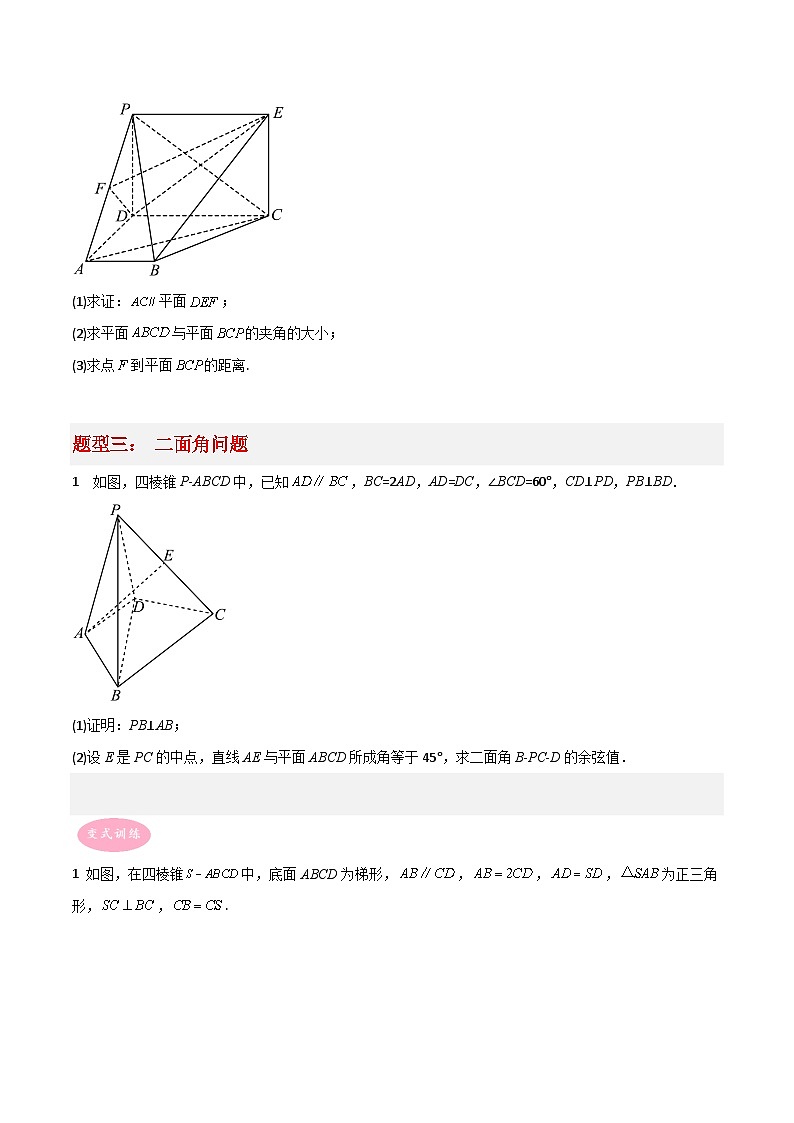
1 如图,在多面体中,已知,,均为等边三角形,平面平面ABC,平面平面ABC,H为AB的中点.
(1)判断DE与平面ABC的位置关系,并加以证明;
(2)求直线DH与平面ACE所成角的正弦值.
1 如图,垂直于梯形所在平面,,为的中点,,,四边形为矩形.
(1)求证:平面;
(2)求平面与平面的夹角的大小;
(3)求点到平面的距离.
题型三: 二面角问题
1 如图,四棱锥P-ABCD中,已知,BC=2AD,AD=DC,∠BCD=60°,CD⊥PD,PB⊥BD.
(1)证明:PB⊥AB;
(2)设E是PC的中点,直线AE与平面ABCD所成角等于45°,求二面角B-PC-D的余弦值.
1 如图,在四棱锥中,底面ABCD为梯形,,,,为正三角形,,.
(1)求证:平面平面SBC;
(2)求二面角的余弦值.
题型四: 空间几何综合问题
1.如图所示,正方形ABCD所在平面与梯形ABMN所在平面垂直,,,,.
(1)证明:平面;
(2)在线段CM(不含端点)上是否存在一点E,使得二面角的余弦值为.若存在,求出的值;若不存在,请说明理由.
1 如图,在四棱锥E-ABCD中,平面ADE⊥平面ABCD,O、M分别为线段AD、DE的中点,四边形BCDO是边长为1的正方形,AE=DE,AE⊥DE.
(1)求证:CM平面ABE;
(2)求直线CM与BD所成角的余弦值;
(3)点N在直线AD上,若平面BMN⊥平面ABE,求线段AN的长.
1.(2023·山东·潍坊一中校联考模拟预测)如图,在四棱锥中,为等边三角形,为的中点,,平面平面.
(1)证明:平面平面;
(2)若,,,求平面与平面夹角的余弦值.
2.(2023·山东·日照一中校考模拟预测)如图,直三棱柱的体积为4,的面积为.
(1)求A到平面的距离;
(2)设D为的中点,,平面平面,求二面角的正弦值.
3.(2023·吉林·长春十一高校联考模拟预测)如图,在三棱柱中,平面ABC,D为线段AB的中点,,,,三棱锥的体积为8.
(1)证明:平面;
(2)求平面与平面夹角的余弦值.
4.(2022·江苏南京·南京师大附中校考模拟预测)如图,在四棱锥中,底面是边长为2的菱形,,为等边三角形,为线段的中点,且平面平面,是线段上的点.
(1)求证:;
(2)若直线与平面的夹角的正弦值为,求四棱锥的体积.
5.(2023·河北衡水·衡水市第二中学校考模拟预测)如图,直四棱柱中,,E是的中点,底面ABCD是平行四边形,若平面.
(1)若,证明:底面是正方形
(2)若,求二面角的余弦值
6.(2022·河北衡水·河北衡水中学校考模拟预测)直四棱柱被平面所截,所得的一部分如图所示,.
(1)证明:平面;
(2)若,,平面与平面所成角的正切值为,求点到平面的距离.
1.(2021·全国·统考高考真题)如图,四棱锥的底面是矩形,底面,,为的中点,且.
(1)求;
(2)求二面角的正弦值.
2.(2021·全国·统考高考真题)已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小?
3.(2021·全国·统考高考真题)如图,在三棱锥中,平面平面,,为的中点.
(1)证明:;
(2)若是边长为1的等边三角形,点在棱上,,且二面角的大小为,求三棱锥的体积.
4.(2022·全国·统考高考真题)如图,四面体中,,E为的中点.
(1)证明:平面平面;
(2)设,点F在上,当的面积最小时,求与平面所成的角的正弦值.
5.(2022·全国·统考高考真题)小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面是边长为8(单位:)的正方形,均为正三角形,且它们所在的平面都与平面垂直.
(1)证明:平面;
(2)求该包装盒的容积(不计包装盒材料的厚度).
6.(2022·全国·统考高考真题)如图,直三棱柱的体积为4,的面积为.
(1)求A到平面的距离;
(2)设D为的中点,,平面平面,求二面角的正弦值.
7.(2022·全国·统考高考真题)如图,是三棱锥的高,,,E是的中点.
(1)证明:平面;
(2)若,,,求二面角的正弦值.
8.(2022·北京·统考高考真题)如图,在三棱柱中,侧面为正方形,平面平面,,M,N分别为,AC的中点.
(1)求证:平面;
(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:;
条件②:.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
9.(2022·天津·统考高考真题)直三棱柱中,,D为的中点,E为的中点,F为的中点.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)求平面与平面所成二面角的余弦值.
专题05 解析几何-冲刺高考数学大题突破+限时集训(新高考专用): 这是一份专题05 解析几何-冲刺高考数学大题突破+限时集训(新高考专用),文件包含专题05解析几何-冲刺高考数学大题突破+限时集训新高考专用解析版docx、专题05解析几何-冲刺高考数学大题突破+限时集训新高考专用原卷版docx等2份试卷配套教学资源,其中试卷共99页, 欢迎下载使用。
专题06 导数及其应用-冲刺高考数学大题突破+限时集训(新高考专用): 这是一份专题06 导数及其应用-冲刺高考数学大题突破+限时集训(新高考专用),文件包含专题06导数-冲刺高考数学大题突破+限时集训新高考专用解析版docx、专题06导数-冲刺高考数学大题突破+限时集训新高考专用原卷版docx等2份试卷配套教学资源,其中试卷共70页, 欢迎下载使用。
专题05 解析几何-冲刺高考数学大题突破+限时集训(新高考专用): 这是一份专题05 解析几何-冲刺高考数学大题突破+限时集训(新高考专用),文件包含专题05解析几何-冲刺高考数学大题突破+限时集训新高考专用解析版docx、专题05解析几何-冲刺高考数学大题突破+限时集训新高考专用原卷版docx等2份试卷配套教学资源,其中试卷共99页, 欢迎下载使用。












