初中数学人教版八年级上册12.1 全等三角形课时练习

全等三角形判定一（SSS，SAS）（提高）

【学习目标】

1．理解和掌握全等三角形判定方法1——“边边边”，和判定方法2——“边角边”；

2．能把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等.

【要点梳理】

要点一、全等三角形判定1——“边边边”

全等三角形判定1——“边边边”

三边对应相等的两个三角形全等.（可以简写成“边边边”或“SSS”）.

要点诠释：如图，如果＝AB，＝AC，＝BC，则△ABC≌△.

要点二、全等三角形判定2——“边角边”

1. 全等三角形判定2——“边角边”

两边和它们的夹角对应相等的两个三角形全等（可以简写成“边角边”或“SAS”）.

要点诠释：如图，如果AB ＝ ，∠A＝∠，AC ＝ ，则△ABC≌△. 注意：这里的角，指的是两组对应边的夹角.

2. 有两边和其中一边的对角对应相等，两个三角形不一定全等.

如图，△ABC与△ABD中，AB＝AB，AC＝AD，∠B＝∠B，但△ABC与△ABD不完全重合，故不全等，也就是有两边和其中一边的对角对应相等，两个三角形不一定全等.

【典型例题】

类型一、全等三角形的判定1——“边边边”

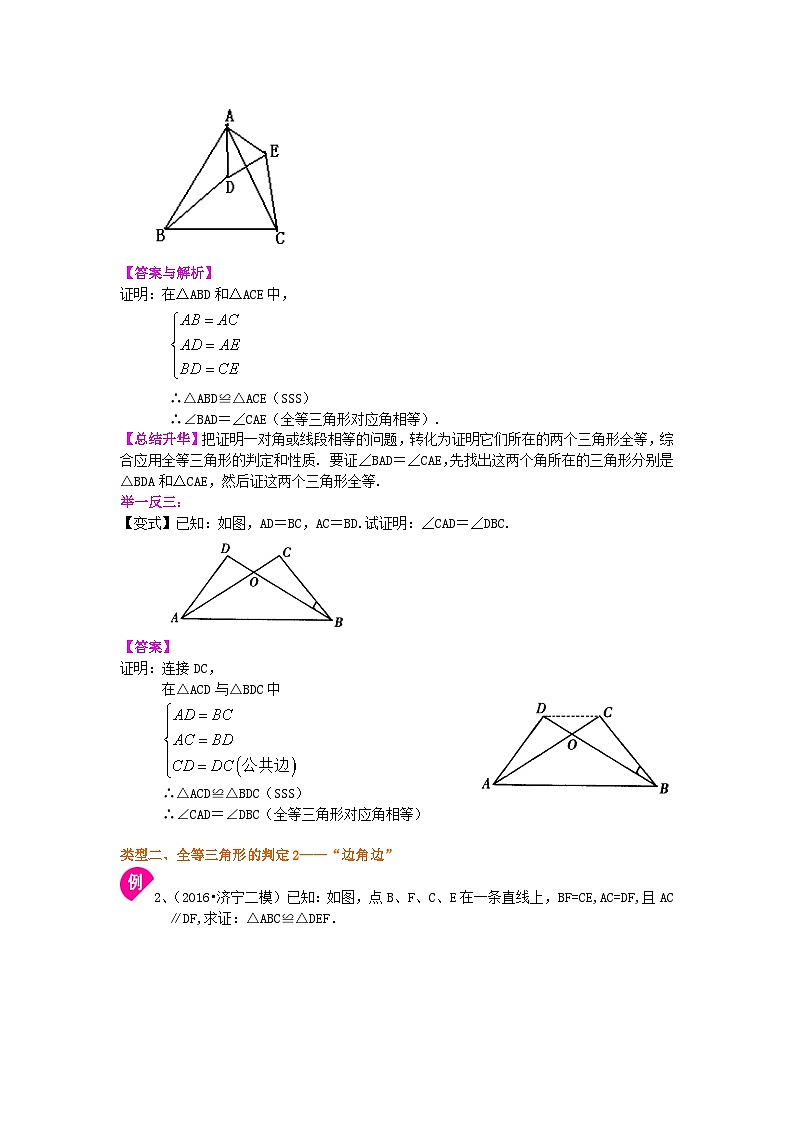
1、如图，在△ABC和△ADE中，AB＝AC，AD＝AE，BD＝CE，求证：∠BAD＝∠CAE.

【答案与解析】

证明：在△ABD和△ACE中，

∴△ABD≌△ACE（SSS）

∴∠BAD＝∠CAE（全等三角形对应角相等）.

【总结升华】把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等，综合应用全等三角形的判定和性质. 要证∠BAD＝∠CAE，先找出这两个角所在的三角形分别是△BDA和△CAE，然后证这两个三角形全等.

举一反三：

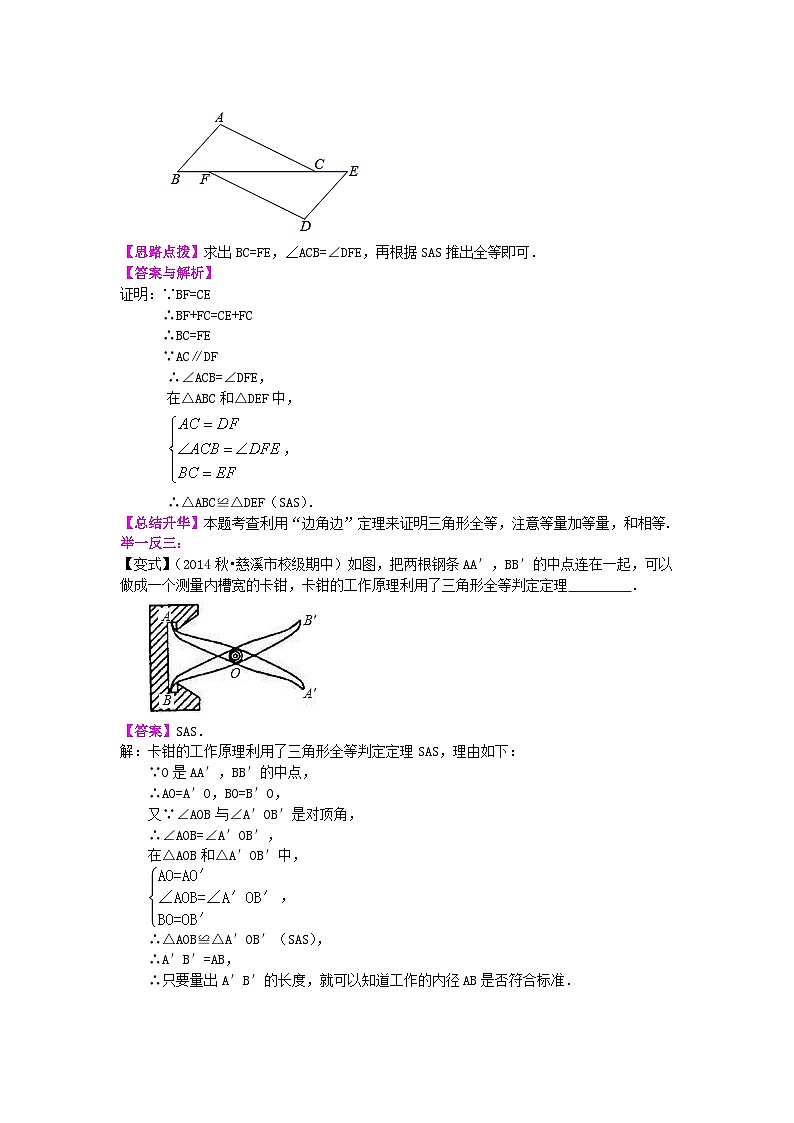
【变式】已知：如图，AD＝BC，AC＝BD.试证明：∠CAD＝∠DBC.

【答案】

证明：连接DC，

      在△ACD与△BDC中

∴△ACD≌△BDC（SSS）

∴∠CAD＝∠DBC（全等三角形对应角相等）

类型二、全等三角形的判定2——“边角边”

2、（2016•济宁二模）已知：如图，点B、F、C、E在一条直线上，BF=CE,AC=DF,且AC∥DF,求证：△ABC≌△DEF．

【思路点拨】求出BC=FE，∠ACB=∠DFE，再根据SAS推出全等即可．

【答案与解析】 

证明：∵BF=CE

∴BF+FC=CE+FC

∴BC=FE

∵AC∥DF

∴∠ACB=∠DFE，

在△ABC和△DEF中，

，

∴△ABC≌△DEF（SAS）．

【总结升华】本题考查利用“边角边”定理来证明三角形全等，注意等量加等量，和相等.

举一反三：

【变式】（2014秋•慈溪市校级期中）如图，把两根钢条AA′，BB′的中点连在一起，可以做成一个测量内槽宽的卡钳，卡钳的工作原理利用了三角形全等判定定理　     　．

【答案】SAS．

解：卡钳的工作原理利用了三角形全等判定定理SAS，理由如下：

∵O是AA′，BB′的中点，

∴AO=A′O，BO=B′O，

又∵∠AOB与∠A′OB′是对顶角，

∴∠AOB=∠A′OB′，

在△AOB和△A′OB′中，

，

∴△AOB≌△A′OB′（SAS），

∴A′B′=AB，

∴只要量出A′B′的长度，就可以知道工作的内径AB是否符合标准．

3、已知，如图：在△ABC中，∠B＝2∠C，AD⊥BC，

求证：AB＝CD－BD．

【思路点拨】在DC上取一点E，使BD＝DE，则△ABD≌△AED，所以AB＝AE，只要再证出EC＝AE即可．

【答案与解析】

证明：在DC上取一点E，使BD＝DE

∵ AD⊥BC，∴∠ADB＝∠ADE

在△ABD和△AED中， BD＝DE，AD＝AD．

∴△ABD≌△AED（SAS）．

∴AB＝AE，∠B＝∠AED．

又∵∠B＝2∠C＝∠AED＝∠C＋∠EAC．

∴∠C＝∠EAC．∴AE＝EC．

∴AB＝AE＝EC＝CD—DE＝CD—BD．

【总结升华】此题采用截长或补短方法.上升到解题思想，就是利用翻折变换，构造的全等三角形，把条件集中在基本图形里面，从而使问题加以解决．如图，要证明AB＝CD－BD，把CD－BD转化为一条线段，可利用翻折变换，把△ABD沿AD翻折，使线段BD运动到DC上，从而构造出CD－BD，并且也把∠B转化为∠AEB，从而拉近了与∠C的关系.

举一反三：

【变式】已知，如图，在四边形ABCD中，AC平分∠BAD，CE⊥AB于E，并且AE＝（AB＋AD），求证：∠B＋∠D＝180°.

【答案】

证明：在线段AE上，截取EF＝EB，连接FC，

∵CE⊥AB，

∴∠CEB＝∠CEF＝90°

在△CBE和△CFE中，

∴△CBE≌△CFE（SAS）

∴∠B＝∠CFE

∵AE＝（AB＋AD），∴2AE＝ AB＋AD

∴AD＝2AE－AB

∵AE＝AF＋EF，

∴AD＝2（AF＋EF）－AB＝2AF＋2EF－AB＝AF＋AF＋EF＋EB－AB＝AF＋AB－AB，

即AD＝AF

在△AFC和△ADC中

∴△AFC≌△ADC（SAS）

∴∠AFC＝∠D

∵∠AFC＋∠CFE＝180°，∠B＝∠CFE.

∴∠AFC＋∠B＝180°，∠B＋∠D＝180°.

类型三、全等三角形判定的实际应用　

4、（2014秋•紫阳县期末）雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE=AB，AF=AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由．

【思路点拨】证角相等，常常通过把角放到两个全等三角形中来证，本题OA=OA公共边，可考虑SSS证明三角形全等，从而推出角相等．

【答案与解析】解：雨伞开闭过程中二者关系始终是：∠BAD=∠CAD，

理由如下：

∵AB=AC，AE=AB，AF=AC，

∴AE=AF，

在△AOE与△AOF中，

，

∴△AOE≌△AOF（SSS），

∴ ∠BAD=∠CAD．

【总结升华】本题考查全等三角形的应用．在实际生活中，常常通过两个全等三角形，得出对应角相等．