





北京课改版九年级下册23.3 轴对称变换复习课件ppt
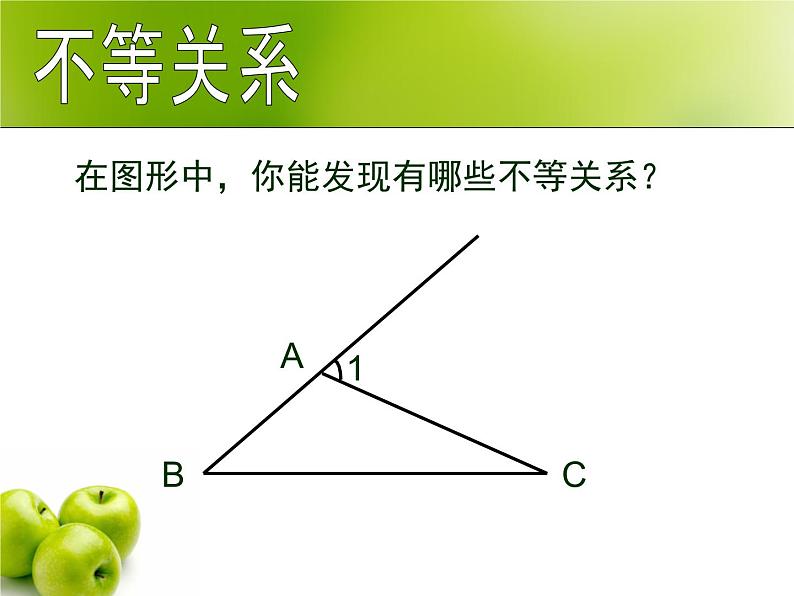
展开在图形中,你能发现有哪些不等关系?
不等关系的基本理论依据
1.三角形两边之和大于第三边,两边之差小于第三边.
2.三角形的一个外角大于与它不相邻的任意一个内角.
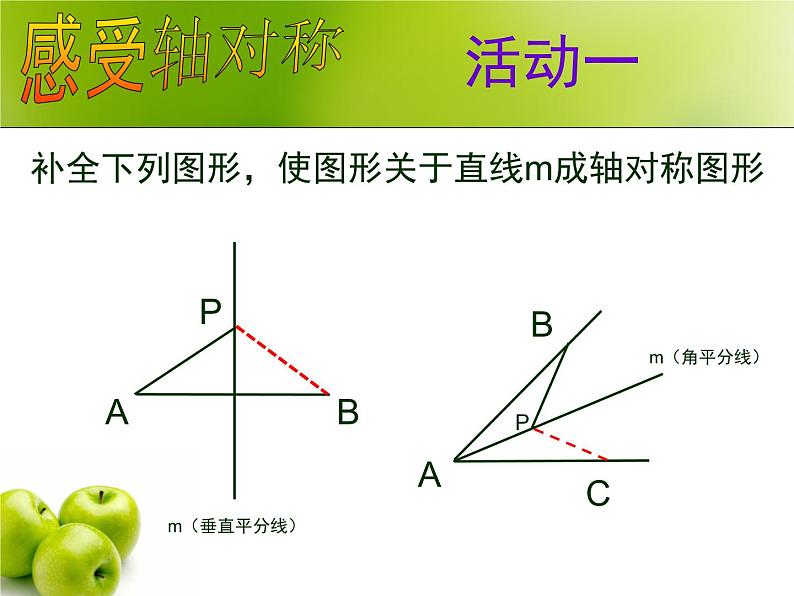
补全下列图形,使图形关于直线m成轴对称图形
在折叠过程中,体现了哪种图形变换?
等腰三角形的两个底角相等
问:在一个三角形中,不相等的边所对的角,它们相等吗?
如图,在⊿ABC中,如果AB˃AC,那么∠C 与∠B有怎样的大小关系?请说明理由.
问:在一个三角形中,不相等的角所对的边,它们相等吗?
如图,在⊿ABC中,如果∠C ˃∠B ,则AB AC. (< 、= 、>)
1.研究不等关系,通过利用轴对称变换,可以达到线段与角的迁移,从而在三角形中,根据不等关系的理论基础,实现问题的解决。
2.若图形中存在有角平分线、垂直平分线,我们往往可以联想到轴对称变换,这也是转化思想的一种体现.
不等关系问题中遇角平分线垂直平分线
1.如图,在⊿ABC中,AD是∠BAC外角平分线,P是AD上异于A的任意一点,连接BP,CP.则BP+CP AB+AC
A.大于 B.等于C.小于 D.无法判断
2.在等腰⊿ABC中,AB=AC,AD⊥BC ,点M是AD上一动点,点E在AC上,连接BE,ME,MC.判断ME+MC与BE有何数量关系,并说明理由.
谈谈这节课你有哪些收获?
自学课本84页实验与探究,完成课文中对应的三道练习.完成作业纸中,课本85页“将军饮马”问题.
2023年浙江省中考数学二轮专题复习:一次函数 复习课件: 这是一份2023年浙江省中考数学二轮专题复习:一次函数 复习课件,共26页。PPT课件主要包含了说说你对它的认识,温故知新,拓展提高,一次函数,一次函数图象和性质,一次函数的应用,概括提炼,或-2,分类讨论思想,巩固应用等内容,欢迎下载使用。
中考数学二轮复习课时讲解课件专题复习(七)《函数与几何综合探究题》(含答案): 这是一份中考数学二轮复习课时讲解课件专题复习(七)《函数与几何综合探究题》(含答案),共60页。PPT课件主要包含了-14,-20,类型8其他问题等内容,欢迎下载使用。
中考数学二轮复习考点精讲课件专题04 规律探究之图形 (含答案): 这是一份中考数学二轮复习考点精讲课件专题04 规律探究之图形 (含答案),共17页。













