

2023年中考数学一轮专题复习课件 全等三角形
展开
这是一份2023年中考数学一轮专题复习课件 全等三角形,共18页。PPT课件主要包含了平移模型,锐角一线三等角,钝角一线三等角,旋转模型,手拉手模型等内容,欢迎下载使用。
1、定义:能够完全重合的两个三角形叫作全等三角形.
①全等三角形的对应边相等,对应角相等;②全等三角形的周长相等,面积相等;③全等三角形对应的中线、高线、角平分线、中位线都相等.
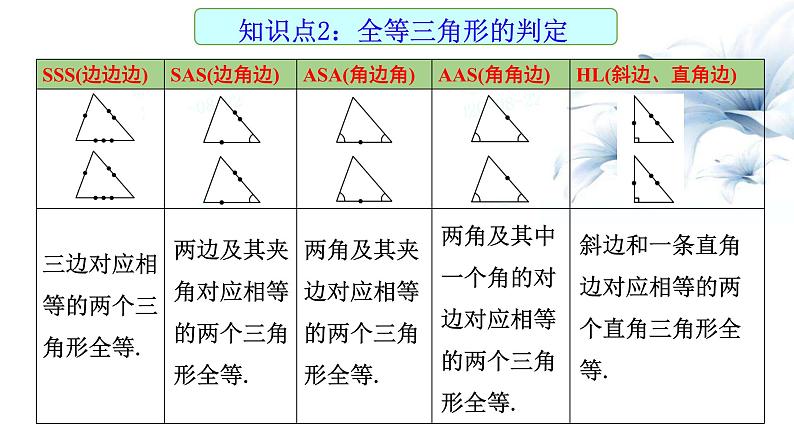
三边对应相等的两个三角形全等.
两边及其夹角对应相等的两个三角形全等.
两角及其夹边对应相等的两个三角形全等.
两角及其中一个角的对边对应相等的两个三角形全等.
斜边和一条直角边对应相等的两个直角三角形全等.
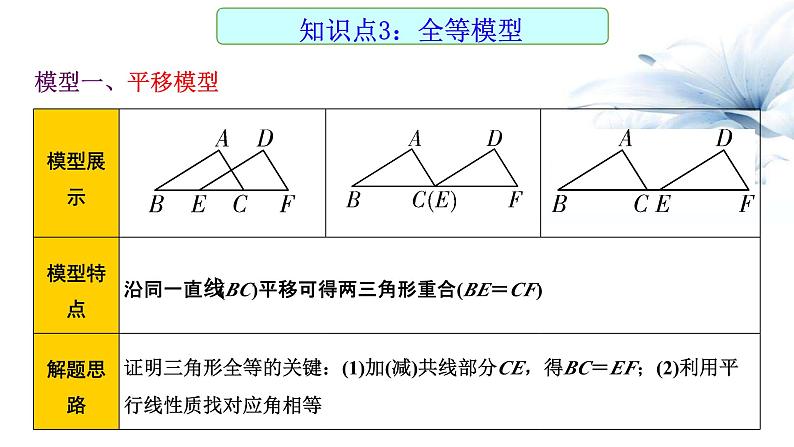
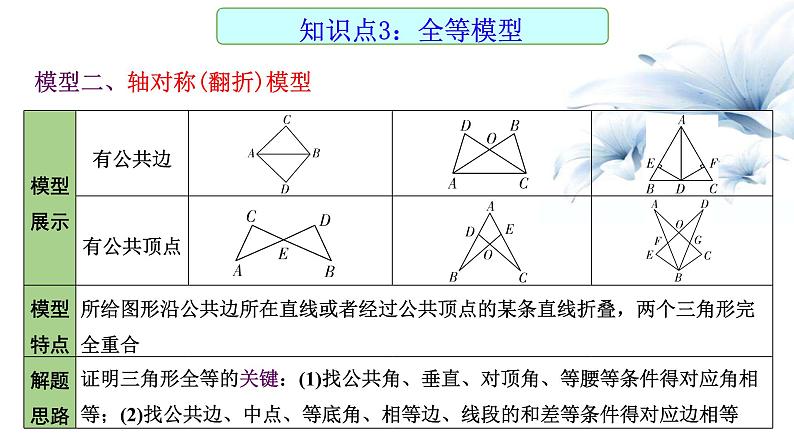
模型二、轴对称(翻折)模型
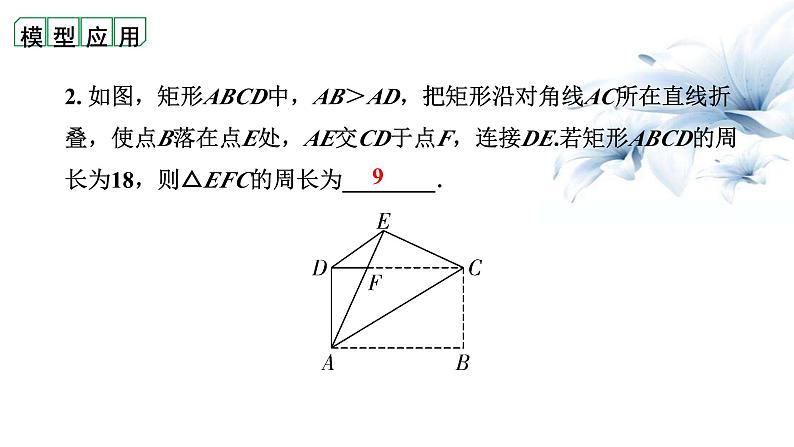
2. 如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.若矩形ABCD的周长为18,则△EFC的周长为________.
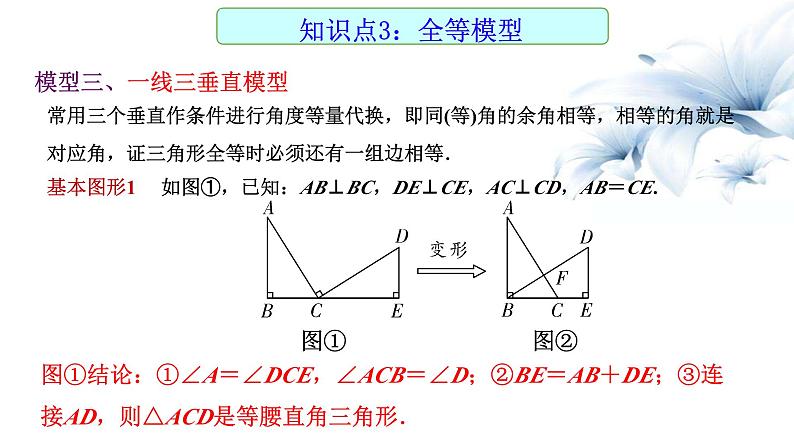
模型三、一线三垂直模型
图① 图②
常用三个垂直作条件进行角度等量代换,即同(等)角的余角相等,相等的角就是对应角,证三角形全等时必须还有一组边相等.基本图形1 如图①,已知:AB⊥BC,DE⊥CE,AC⊥CD,AB=CE.
图①结论:①∠A=∠DCE,∠ACB=∠D;②BE=AB+DE;③连接AD,则△ACD是等腰直角三角形.
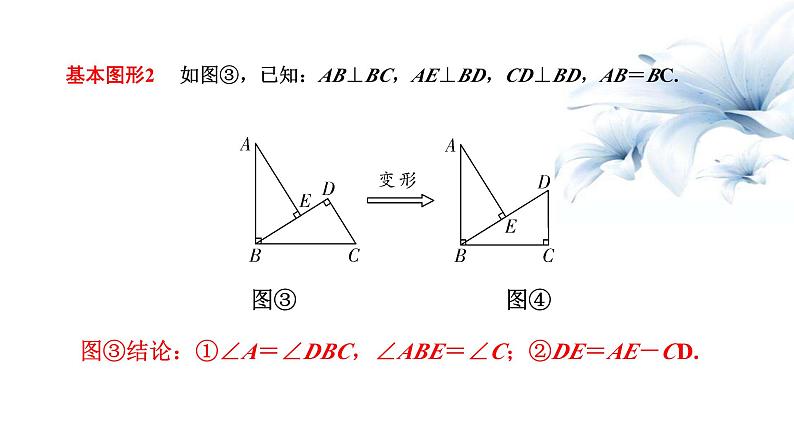
基本图形2 如图③,已知:AB⊥BC,AE⊥BD,CD⊥BD,AB=BC.
图③ 图④
图③结论:①∠A=∠DBC,∠ABE=∠C;②DE=AE-CD.
3. 如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2. 求证:△ADE≌△BEC;
证明:∵AD∥BC,∠A=90°,∠1=∠2,∴∠A=∠B=90°,DE=CE.在Rt△ADE和Rt△BEC中,∴Rt△ADE≌Rt△BEC(HL);
模型四、一线三等角模型
一般通过一线三等角找等角或进行角度转换,证三角形全等时必须还有一组边相等这个条件. 常见基本图形如下:1.两个三角形在直线同侧,点P在线段AB上,已知:∠1=∠2=∠3,AP=BD.
结论:△CAP≌△PBD.
2.两个三角形在直线异侧,点P在BA(或AB)的延长线上,已知:∠1=∠2=∠3,CP=PD.
结论:△CAP≌△PBD.
4. 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且BP=CD,∠APD=∠B,若∠APB=120°,则∠CDP的度数为( )A. 30° B. 60° C. 120° D. 150°
5. 如图,在△ABC中,AB=AC,点D,E分别在AC及其延长线上,点B,F分别在AE两侧,连接CF,已知AD=EC,BC=FD,BC∥DF. (1)求证:△ABC≌△EFD;
(1)证明:∵AD=EC,∴AD+DC=EC+DC,即AC=ED,∵BC∥DF,∴∠ACB=∠EDF.在△ABC和△EFD中,∵BC=FD,∠ACB=∠EDF,AC=ED,∴△ABC≌△EFD(SAS);
模型七、对角互补模型
7. 如图,在等边△ABC中,点D是线段BC的中点,∠EDF=120°,射线DE与线段AB交于点E,射线DF交AC于点F,求证:DE=DF.
相关课件
这是一份专题10 全等三角形-中考数学一轮复习课件PPT,共37页。PPT课件主要包含了全等三角形,对应角相等,对应边相等,周长相等,ASA,AAS,SAS,SSS,常见的几种辅助线添加,考点3角平分线等内容,欢迎下载使用。
这是一份中考数学复习专题:全等三角形 课件PPT,共39页。PPT课件主要包含了AAS,ASA,答案相等,对应的中线,对应的角平,答案题设,真命题,假命题,全等三角形的性质,A72°等内容,欢迎下载使用。
这是一份全等三角形复习 -中考数学一轮复习课件,共14页。PPT课件主要包含了思路点拨,能力提升,方法点拨,真题演练,课堂小结等内容,欢迎下载使用。








